🚀 What I Will Learn

• 인덱스 트리(Indexed Tree)에 대해 이해하기
• 인덱스 트리를 활용하여 구간 합을 구하는 방법 학습하기

인덱스 트리(Indexed Tree)란? 구간 합을 구하는 트리의 종류로 인덱스 트리, 세그먼트 트리, 펜윅 트리가 있다. 세그먼트 트리는 인덱스 트리가 포함하고 있는 한 종류이다.

---

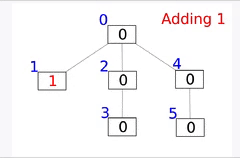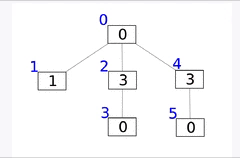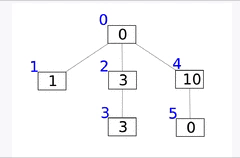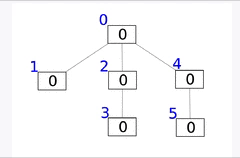
인덱스 트리(Indexed Tree)

✔️ 트리 구조로 구간 합 구하기

• 세그먼트 트리는 구현하는 과정이 복잡하고 어렵다는 단점이 있다
• 인덱스 트리는 구현이 매우 간단하다
• 인덱스 트리를 활용하여 구간합을 구하는 과정도 𝑂(𝑙𝑜𝑔𝑁)의 시간 복잡도를 가진다
• 인덱스 트리는 세그먼트 트리에 비해서 메모리 효율성이 높다

1️⃣ 인덱스 트리(Indexed Tree)란?

✔️ 특정한 숫자의 마지막 비트 구하기

• 특정한 숫자 A의 가장 마지막 비트를 구하고자 할 때는 A & -A를 구하면 된다
  • 예시) A가 14일 때 비트 형태로 표현하면 이렇다

✔️ 마지막 비트를 이용해 트리 구조 만들기

• 각 인덱스에 대해 마지막 비트를 내가 저장하고 있는 값들의 갯수로 계산한다

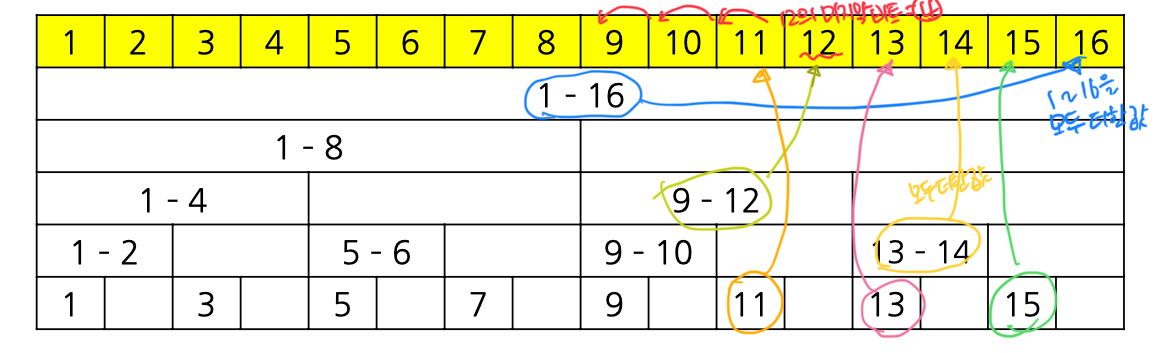
✔️ 인덱스 트리: 1부터 N까지의 구간 합 구하기

• 예시) 인덱스 1~13까지

1) 마지막 비트만큼 구간을 앞으로 이동하며 합 구하기

---

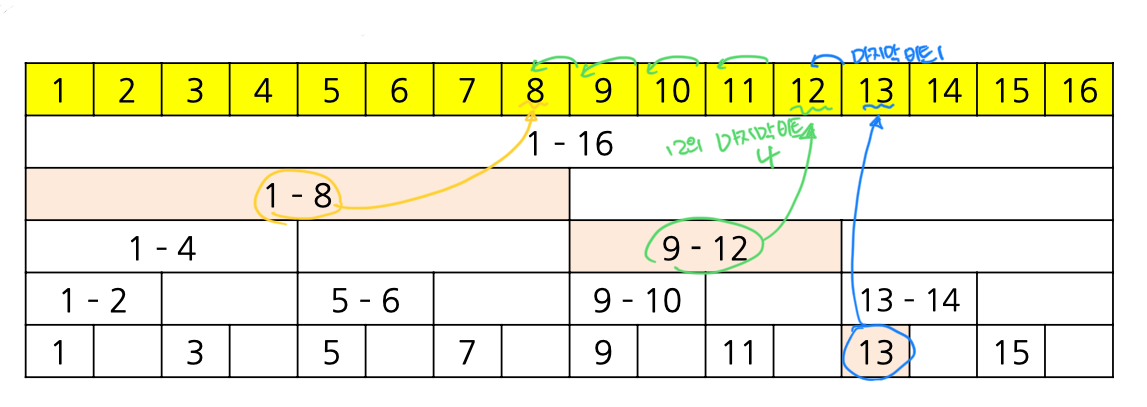
✨ tl;dr

• 인덱스 트리에서의 구간 합 계산 및 원소 수정 과정은 𝑂(𝑙𝑜𝑔𝑁)의 시간 복잡도를 가진다

시간복잡도: 문제를 해결하는데 걸리는 시간과 입력의 함수 관계.
컴퓨터과학에서 알고리즘의 시간복잡도는 입력을 나타내는 문자열 길이의 함수로서 작동하는 알고리즘을 취해 시간을 정량화하는 것을 의미