[프로그래머스] 쌍둥이 빌딩 숲 javascript

이 글은 _jake님의 풀이를 보고 이해한 내용을 바탕으로 작성한 글입니다

대전제

쌍둥이 빌딩은 높은 것부터 놓는다고 가정합니다.
쌍둥이 빌딩을 높은 것부터 두면 그 뒤에는 해당 빌딩보다 낮은 건물들만 올 수 있기 때문입니다.

초기 선언

측면에서 보이는 빌딩의 개수에 대해서 배열을 선언합니다 array[i]라고 하면 array[i]는 측면에서 보이는 i개의 빌딩 수에 대한 경우의 수 입니다.

가장 기본적으로 쌍둥이 빌딩 1채에 대해서 측면 빌딩 수가 1개로 보이는 경우의 수는 하나밖에 없으므로 초기 array[1]의 값은 1로 설정합니다.

규칙 찾기

일단 쌍둥이 빌딩 한 채를 놓고 두 번째 쌍둥이 빌딩을 놓는다고 가정합니다. 쌍둥이 빌딩을 놓을 수 있는 방법은 총 두 가지 입니다.
1. 맨 앞에 넣기
2. 빌딩 사이에 넣기 + 맨 뒤에 놓기

💡 여기서 모든 빌딩 사이에 넣는 것이(2번이) 가능한 이유는 대전제가 있기 때문입니다 높은 건물을 배치하고 그 사이에 더 낮은 건물을 넣어야 규칙에 어긋나지 않습니다.

1. 맨 앞에 넣기
   이 경우 건물은 [1,1,2,2]로 쌓입니다. 측면에서 보게 되면 건물의 개수는 둘(증가함)이 되고 [1,1,2,2]외에 가능한 것은 없습니다.

2. 빌딩 사이에 넣기
   이미 놓인 빌딩이 [2,2]라고 한다면 [2,1,1,2], [2,2,1,1]이 가능합니다. 이 경우 측면에서 보이는 건물의 개수는 하나(증가하지 않음)고 경우의 수는 2가 추가 됩니다.

이 중 두 번째 법칙을 좀 더 일반화 해보겠습니다. 만약 n번째 빌딩이 왔을 때 이 빌딩을 넣을 수 있는 곳은 얼마나 될까요? 넣을 수 있는 공간을 별로 표시합니다.

1. (n = 2) 두 번째 빌딩을 넣을 공간 : 2곳(🏢⭐️🏢⭐️)
2. (n = 3) 세 번째 빌딩을 넣을 공간 : 4곳 (🏢⭐️🏢⭐️🏢⭐️🏢⭐️)
3. (n = 4) 네 번쨰 빌딩을 넣을 공간 : 6곳 (🏢⭐️🏢⭐️🏢⭐️🏢⭐️🏢⭐️🏢⭐️)

이렇게 대입하면 2번에 대한 일반적인 식 2 * (n - 1)을 유추해낼 수 있습니다.

1번 규칙에선 측면 건물의 개수가 증가하고 2번 규칙에선 그대로이기 때문에, 두 규칙을 합하면 array[i] = array[i-1] + array[i] * 2 * (n -1) 이란 일반식을 얻어낼 수 있습니다.

문제풀이

이 일반식을 통해 이제 코드를 작성해야 합니다. 특히 여기서 어떻게 반복할 것인지를 이해하는 것이 가장 어려웠습니다.😂😂

아래 도식을 참고하면서 설명하도록 하겠습니다.

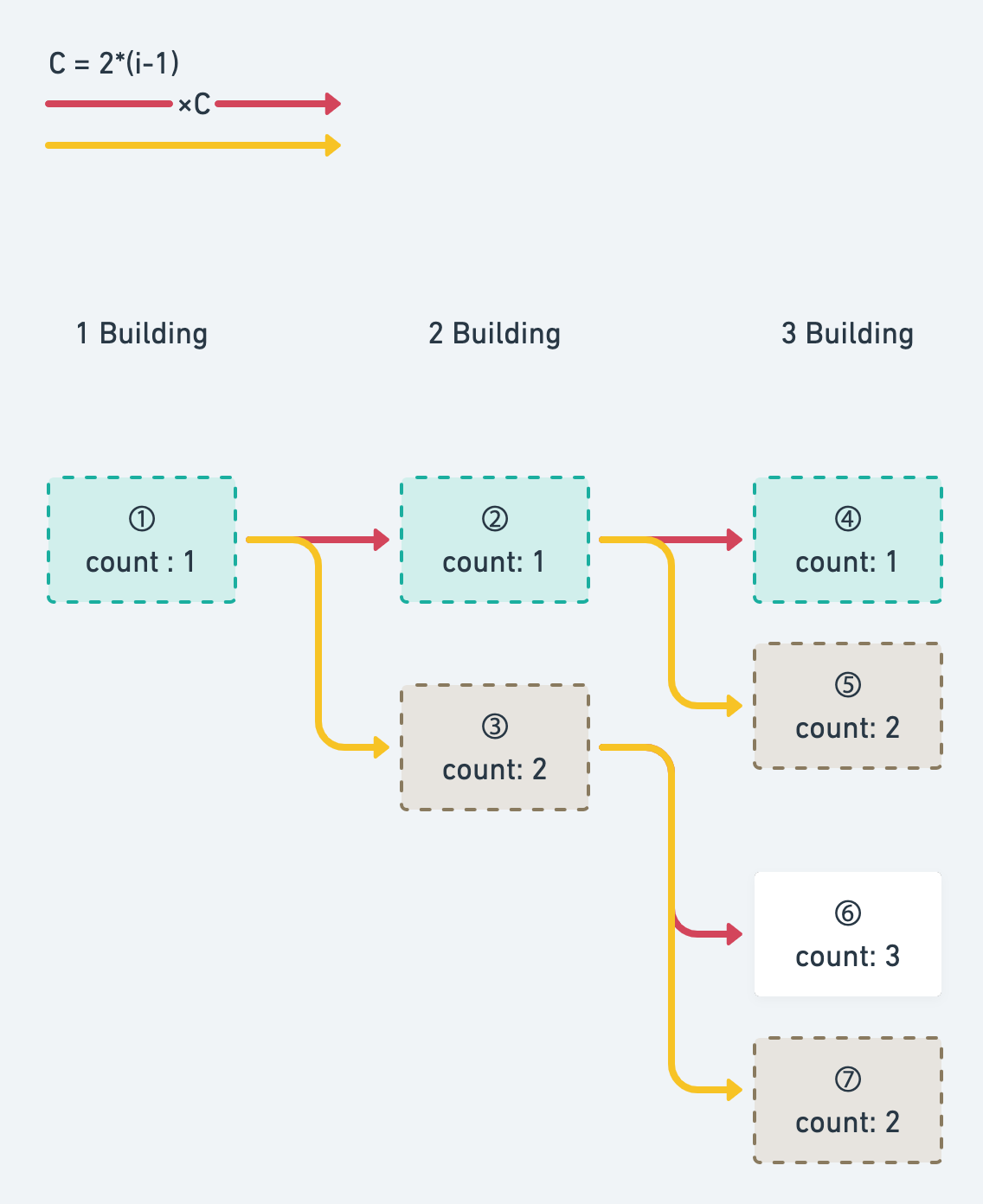
규칙 1은 노란 화살표, 규칙 2는 빨간 화살표를 나타냅니다. 앞 선 규칙을 이해했다면 충분히 이해할 수 있습니다.

필요한 값

여기서 우리가 구하고자 하는 것을 빌딩이 3개 일 때 측면 빌딩의 수가 2개인 것이라 해보겠습니다. 즉, 5번과 7번 노드의 합입니다. 5번과 7번 노드를 구하려면 선행된 노드들을 먼저 알아야 정답을 계산할 수 있습니다.

아까 구한 일반식 array[i] = array[i-1] + array[i] * 2 * (n -1)과 함께 생각해봅시다. 선행 노드를 알기 위해선 어떤 것들이 필요할까요? n과 i값이 필요합니다. n은 빌딩의 개수 i는 측면 빌딩의 개수 입니다.

풀이 과정

1. 노드 1번

이건 이미 array[1] = 1로 했기 때문에 따로 계산이 필요없습니다.

2. 노드 2번과 3번

이 때 n = 2입니다. 그리고 i는 각각 2,1로 두면 될 것 같습니다. 지금은 측면 빌딩이 2까지 구하기로 했으므로, i의 최대값은 2입니다(array = 0은 0으로 합니다. 측면 빌딩이 없는 경우는 0입니다).

1. (n = 2, i = 2) ➡️ array[2] = array[1] = 1 + array[2] = 1 * 1 = 1
2. (n = 2, i = 1) ➡️ array[1] = array[0] = 0 + array[1] = 1 * 2 = 2

💡i를 역순으로 계산하는 이유는 기존의 1번 노드를 기준으로 계산해야하기 때문입니다 순서를 바꿔버릴 경우 2번 노드를 통해 3번 노드를 계산하는 것이므로 적절하지 않습니다.

3. 노드 5번과 7번

1. (n = 3, i = 2) ➡️ array[2] = array[1] = 2 + array[2] = 1 * 4 = 6
2. (n = 3, i = 1) ➡️ array[1] = array[0] = 0 + array[1] = 2 * 4 = 8

따라서 정답은 6이 됩니다.

정답 코드는 원문을 참고해주세요. 코테 준비하는 모든 분들께 도움이 되길 바랍니다. 오타나 오류가 있다면 댓글로 알려주시길 바랍니다!