설날도 지나고 더 힘내야 하는데...도저히 힘이 나질 않는것 같다. 그래서 오늘도 알고리즘 문제 하나 올린다...

서론

우리나라에서 대부분의 취준생은 백준 온라인 저지에서 알고리즘 연습을 한다. 몇가지 단점을 제외하면 정말 좋은 사이트라고 본다. 일단 문제의 양도 상당히 많고, 아주 심플한 UI로 문제 자체에 집중하기 좋은 구조라고 생각된다. 테스트 케이스의 갯수나, 몇개나 맞았는지에 대한 정보가 없다는 건, 결국 코딩테스트 볼때는 모를 정보이므로 감수할 수 있다고 생각할 수도 있고.

다만 백준에서는 항상 입력과 출력의 형식으로 문제가 주어진다. 이게 아쉬운 부분이 무엇이냐면, 그야말로 알고리즘, 즉 Competitive Programming에 초점이 맞춰져 있다는 것이다. 물론 없데이트 중이지만 자체적으로 관리하는 단계별 문제들도 있고, 아예 난이도 공유를 위한 solved.ac도 있지만 결국 이들은 문제를 해결하는게 주요 포인트라는 것이다. 그래서 만약 연결 리스트의 특징을 활용한 문제, 예를들어 "연결 리스트에 사이클이 존재하는지 확인해 주세요"라는 문제를 제시하고자 할때, 입출력을 어떻게 주어야 할지가 명확하지 않다는 것이다.

그래서 solved.ac 기준으로 상위 10개 태그가 전부 골드에 진입한 와중에도, 위에서 언급한 문제를 처음 만났을 때는 조금 신기했었다. 백준에서 풀던 문제들에서는 마주하기 힘들었던 문제였으니까. 그래서 일단 내가 아는 걸로만 해보자는 생각으로 접근했다가 정답이 완전 느리다는 결과가 나오고 나서야 플로이드의 토끼와 거북이 알고리즘 등에 대해 찾아보게 되었다.

어쨋든 알고리즘에 대한 관심이 "취업을 위해서 공부한다!" 보다 좀더 구체적이라면 LeetCode나 Hackerrank 등 다른 해외 사이트에서 문제를 풀어보는 것도 재밌는 것 같다. 지금은 Grind 75 라는 유명한 문제모음을 따라가고 있는데, 오늘의 이야기는 여기서 만난 연결 리스트의 뒤에서 N번째 노드 제거하기라는 문제이다.

문제 보기

만약 LeetCode가 영어라서 겁나는 분들이 계시다면....솔직히 백준 스타일로 문제가 나오면 영어가 걱정될만 하다. 문제를 독해하는데만 한참이 걸리니까. 하지만 개인적인 의견으로 LeetCode는 불필요하게 "철수가 식당에 갔는데..."하는 방식으로 시작하는 문제는 잘 못보고, "트리에서 어떤 노드를 찾아주세요", "배열에 중복인 원소가 존재하는지 찾아주세요"라는 등 굉장히 직관적인 문제들이 많아서 영어를 잘 못해도 번역기만 돌려도 되는 수준이다. 아무튼 그래서, 복붙하기는 조금 그러니까...다음 그림은 연결 리스트를 나타낸 모습이다.

우리는 이런 연결 리스트의 head(제일 앞 노드)와 n(n번째)를 인자로 받아서, 뒤에서 $n$번째 노드를 제거한 연결 리스트의 head를 돌려주는 문제이다. 즉 저 연결 리스트의 head가 인자로 들어오고 n이 3이라면, 뒤에서 3번째 노드를 제거한 다음,

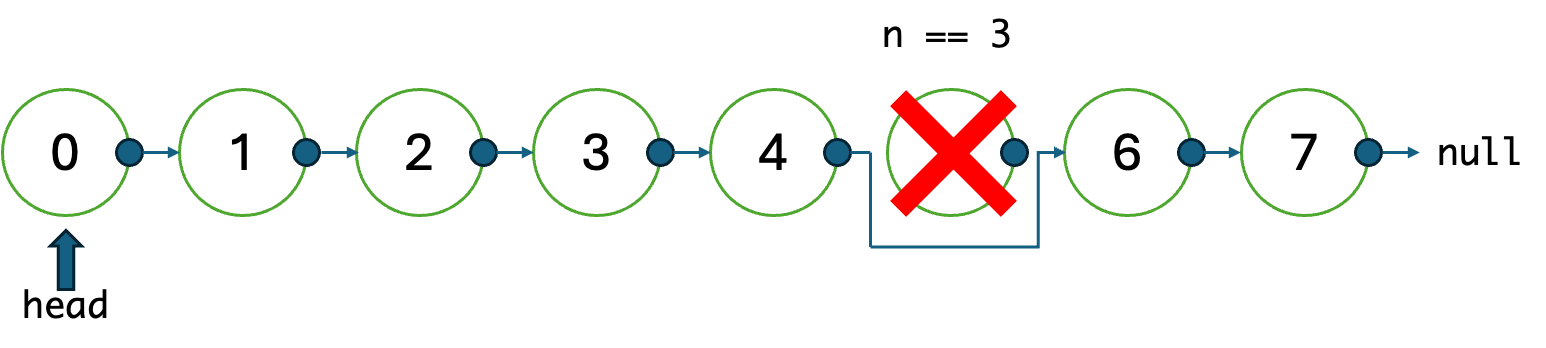
head를 다시 반환하는 것이다. 여기서 노드는 Python을 기준으로 다음과 같이 주어진다.

# Definition for singly-linked list.
class ListNode:
    def __init__(self, val=0, next=None):
        self.val = val
        self.next = next
        

사실 문제를 푸는것 그 자체가 목적이라면 아주 단순하게, 전체 노드의 갯수를 세기만 하면 된다. 전체 노드의 갯수를 센 다음, 뒤에서 $n$번째가 앞에서 몇번째인지만 판단하면 되니까. 근데 LeetCode에서는 이런 간단한 BF적 풀이가 존재하는 문제들에 대하여, 일종의 코멘트?를 단다.

Could you do this in one pass?
구글 번역기: 이걸 한 번에 할 수 있나요?

한번에? 조금 미묘한 번역이긴 하다. 하지만 앞의 해결법을 생각해보면 무슨 말인지 이해가 된다. 우리의 기초 전략은 다음과 같았다.

1. 전체 연결 리스트를 끝까지 확인하면서, 노드의 갯수를 센다.
2. 노드의 갯수를 바탕으로 뒤에서 $n$에 해당하는 위치 $i$를 찾는다.
3. 다시 연결 리스트를 돌면서 $i$번째 노드를 제거한다.

이렇게 될 경우 만약 $n$이 작은 값이었다고 하면, 예를 들어 1이나 2라면, 사실상 연결 리스트를 두번 완전 탐색을 해야한다. LeetCode에서 말하는 pass는 이걸 말하는 건데, 연결 리스트를 두번 탐색하지 말고 한번만 탐색해서 목표를 달성하라는 뜻이었다.

물론 시간 복잡도는 $n$번 탐색하나 $2n$번 탐색하나 $O(n)$이라는걸 알고는 있지만, 뭔가 아쉬운 감정에 다른 해결책을 탐색해 나갔다.

방안 1

옛날 옛적에 자료구조 강의를 들으면서 나왔던 과제가,

C로 구현된 연결 리스트 구조체를 양방향 연결 리스트 구조체로 바꾸고, 그 장단을 정리할 것

이었다. 그래서 양방향 연결 리스트를 구현해 보고, 십만개의 데이터를 넣은 다음 앞뒤로 노드를 탐색해 보았었는데, 양방향 연결 리스트의 경우 나의 현재 노드를 가르키는 포인터를 앞으로도 뒤로도 이동시킬 수 있어서 특정 상황에서는 단방향 연결 리스트보다 헐씬 빠르다고 작성했다. 나중에 성적을 확인해보니 중간 과제 + 시험은 뒤에서 1~2등 해서 말아먹었는데, 기말 과제 + 시험은 앞에서 1~2등 함으로서 결국 A를 사수할 수 있었다. (재수강이라 +은 불가했다)

여기서 착안한 방법은, 앞쪽 노드로 돌아가기 였다. 내가 제거하고 싶은 노드가 뒤에서 $n$번째라면, 일단 끝까지 간 다음 돌아갈 수 있다면 해결책이 헐씬 간단해지고, 탐색 자체도 한번(?)만 하면 될것이다.

한가지 문제라면, 이 연결 리스트는 단방향 연결 리스트 라는 것인데, 그래서 마지막으로 지나온 노드가 먼저 나올 수 있도록 Stack을 활용하면 어떨까? 라고 생각하며 진행하였다.

class Solution:
    def removeNthFromEnd(self, head: Optional[ListNode], n: int) -> Optional[ListNode]:
        # 노드가 하나인 리스트
        if not head.next:
            return None

		# 돌아올 노드를 담는 Stack
        stack = []
        now = head
        # 끝까지 간다
        while now:
            stack.append(now)
            now = now.next

		# n만큼 돌아온다
        for i in range(n):
            now = stack.pop()

		# 만약 나보다 앞이 없다면 (n과 연결리스트의 길이가 같다면)
        if not stack:
        	# 다음 노드가 새로운 head다
            return now.next

		# 나보다 하나 앞의 노드와
        front = stack.pop()
        # 내 뒤의 노드를 연결한다.
        front.back = now.back

        return head

그랬더니 잘 된다! 사실 요건 글을 쓰기 시작하면서 떠오른 아이디어 인데, 왜인지 모르게 문제를 풀었던 날에는 딱 떠오르지 않았었다...

다만 요 방법도 최악의 경우엔 리스트의 노드 갯수 * 2 만큼의 탐색이 이뤄지는데, 만약 주어진 $n$이 연결 리스트의 노드 갯수와 동일하다면 뒤로 간 만큼 앞으로 다시 가야하기 때문이다!...만 어차피 시간복잡도는 $O(n)$이다. 시간 복잡도의 함정일라나? 다만 코드 자체는 정말 깔끔한듯.

방안 2

이건 한번의 탐색에 너무 집중한 나머지 엄청 어렵게 풀려고 하였던 방법이다. 여기서는 위에서 소개드린 토끼와 거북이 알고리즘을 응용하였다.

1. 한번에 두 개의 노드를 이동하는 빠른 포인터와, 한 개의 노드를 이동하는 느린 포인터를 준비한다.
2. 각 포인터를 $n$번 이동시킨다. 이러면 느린 포인터는 $n$번째 노드에, 빠른 포인터는 $2n$번째 노드에 위치하게 된다. 즉, 둘 사이의 거리가 $n$이 된다.
3. 빠른 포인터의 속도를 줄여(한번에 한 개의 노드씩), 끝(null)에 닿을 때까지 두 포인터를 같이 움직인다.
4. 그러면 느린 포인터의 위치가 제거한 노드가 된다!

그러니까 0~6의 숫자가 붙은 노드가 있는 상황에서,

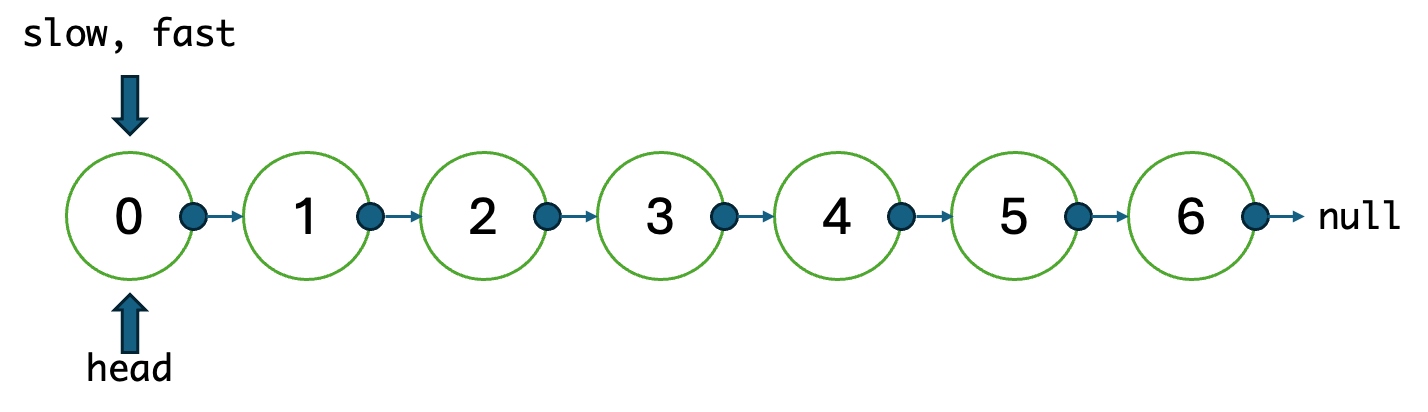
$n = 2$ 라면, 느린 포인터는 2, 빠른 포인터는 4에 도달하도록 2번 움직인 다음,

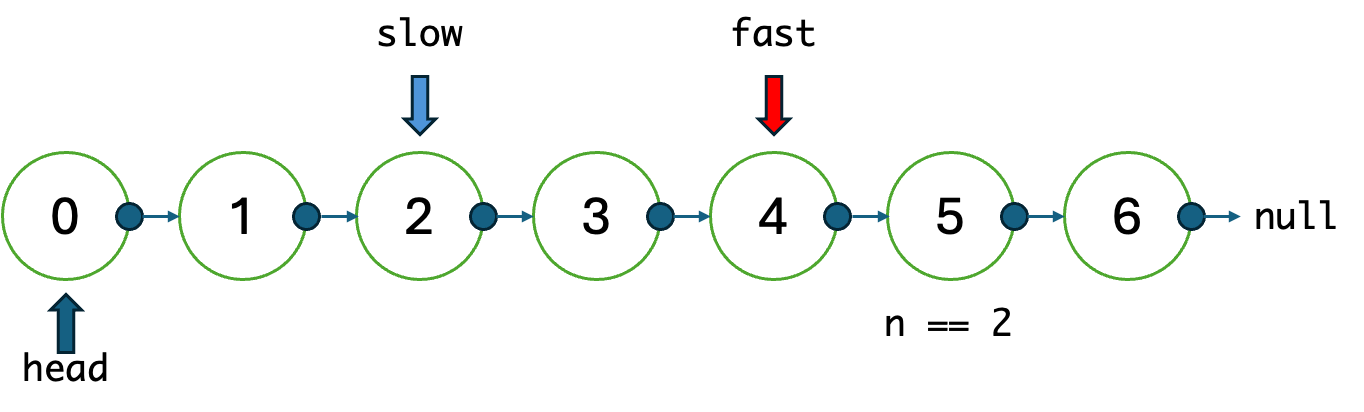
그대로 빠른 포인터와 느린 포인터를 계속 한칸씩만 이동하면?

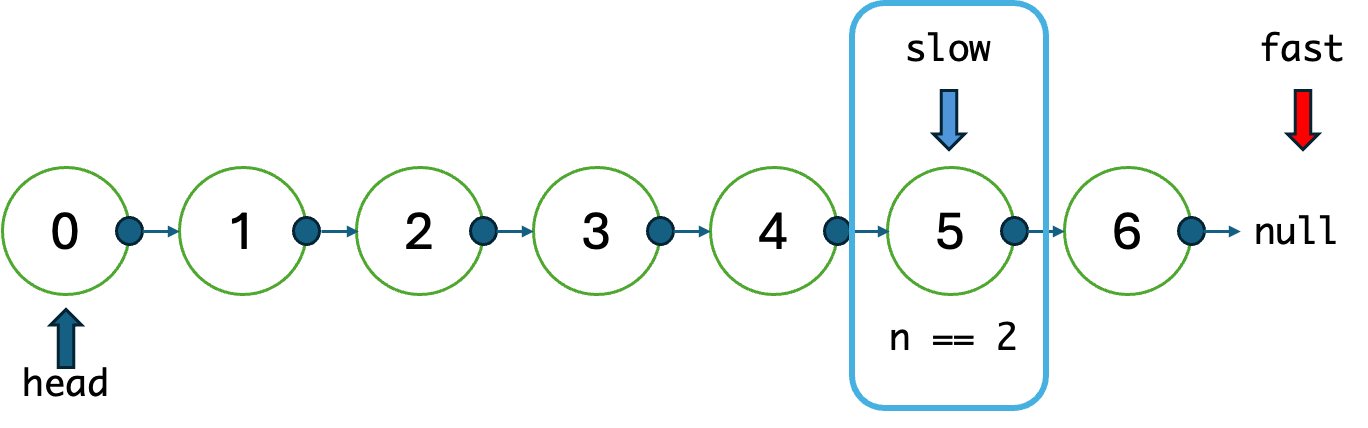
최종적으로 리스트가 끝난 시점의 느린 포인터의 위치가 뒤에서 $n$이 된다는 소리!

문제는 $n$번 이동하기 전에 리스트가 끝나버린 경우였다. 예를 들어 앞의 0~6의 노드가 있는 상황에서 $n = 5$라면, 총 3번 이동하면, 빠른 포인터는 이미 리스트의 끝인 6에 도달하게 되며, 느린 포인터는 목표 노드를 지나치게 되는 것이었다.

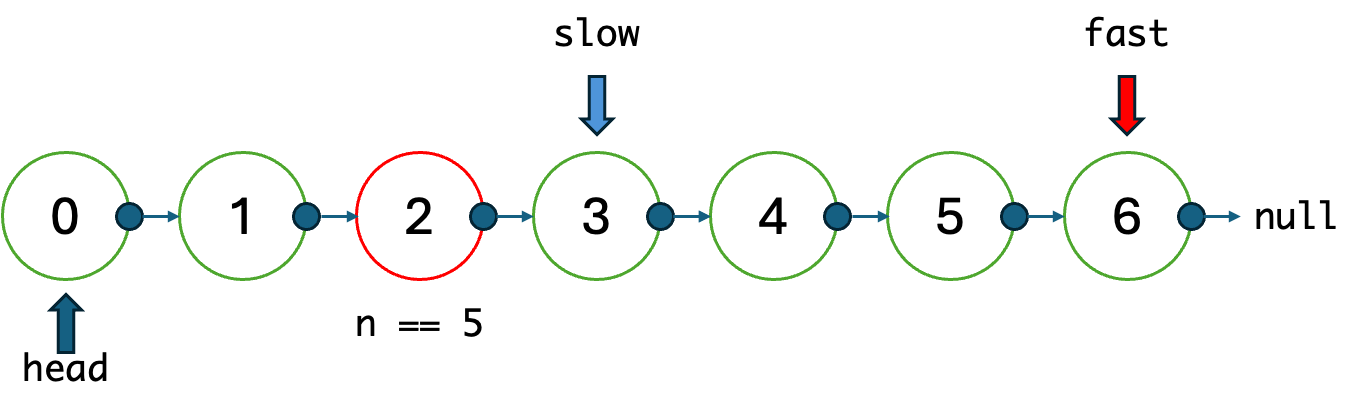
그래도 느린 포인터의 위치는 항상 전체 길이의 절반 지점에서 멈추게 된다는 것이 위안이었다. 그게 무슨 말이냐면, 결국 3번 이동해서 중간의 위치라는 것은 앞에서도 뒤에서도 3(+1)번째라는 것이며, 그걸 기준으로 남은 이동의 횟수만큼 앞으로 이동하면 된다는 것이었다!

실제로는 노드의 갯수가 짝수인지 홀수인지에 따라 느린 포인터가 정확히 중앙인지, 아니면 뒷쪽 절반의 첫 노드인지가 달라지게 된다. 짝수개의 노드라면 정중앙 노드는 존재하지 않으니까.

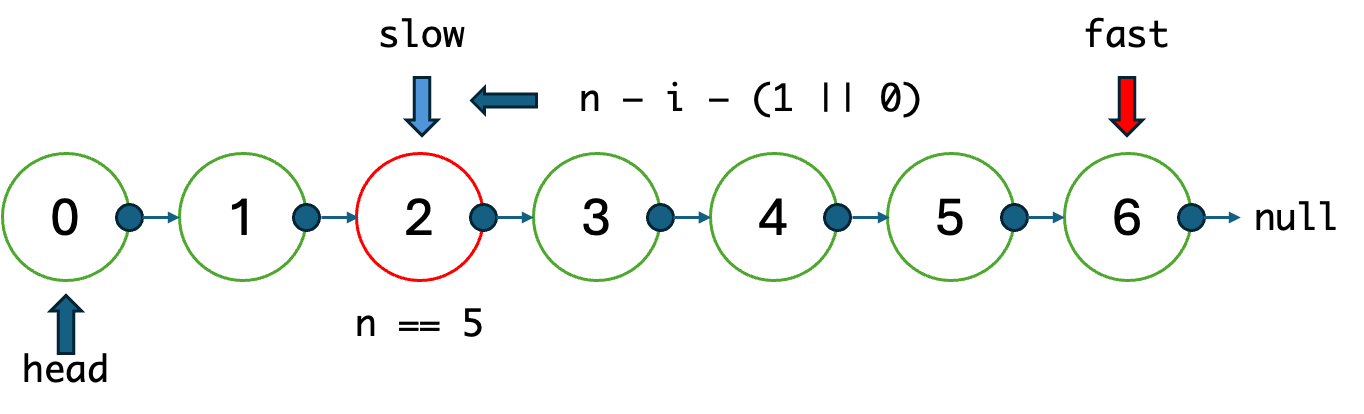
어쩌다보니 이 풀이도 Stack을 필요로 하긴 했다. 이러한 것들을 고려하여 코드를 작성하기 시작했다.

class Solution:
    def removeNthFromEnd(self, head: Optional[ListNode], n: int) -> Optional[ListNode]:
        # 노드가 하나인 리스트
        if not head.next:
            return None

		# 토끼와 거북이
        fast = head
        slow = head

        idx = 0
        stack = []
        # 우선 n번 이동을 시도한다.
        while idx < n:
            # 만약 토끼가 제일 뒤이거나(fast.next is None)
            # 뒤를 지나치게(fast is None) 되었으면 중단한다.
            if not (fast and fast.next):
                break

            # 그게 아니라면 이동한다.
            fast = fast.next.next
            # 느린 포인터의 노드는 되돌아가기 위해 저장을 먼저 하고,
            stack.append(slow)
            # 돌아간다.
            slow = slow.next
            idx += 1

        # 만약 n번 이동하는데 성공했다면,
        if idx == n:
            # 우선 제일 마지막에 방문한 노드를 꺼내온다.
            # 이는 후에 노드가 제거될 때 연결할 앞의 노드를 가르키는 포인터이다.
            before = stack.pop()
            # 빠른 포인터를
            while fast:
                # 속도를 늦춰서 끝까지 간다.
                fast = fast.next
                # 느린 포인터를 이전 포인터로 지정하고,
                before = slow
                # 느린 포인터도 이동한다.
                slow = slow.next

            # 이제 느린 포인터가 가르키는 노드를 제거한다.
            before.next = slow.next
            return head

        # n번 이동하기 전 빠른 포인터가 끝에 도달할 경우, 얼마나 앞으로 돌아갈지를 결정한다.
        # 이 때 빠른 포인터가
        # 1. 마지막 노드면 (idx)번째 노드는 뒤에서 (idx+1)번째 노드이고, (마지막 노드가 1번째 이기 때문)
        # 2. 마지막 노드 다음(None)이면 (idx)번째 노드는 뒤에서 (idx)번째 노드이다.
        # 이를 고려하여 offset을 결정한다. (빠른 포인터가 None이 아니면 한칸 덜가도 된다)
        offset = n - idx - (1 if fast else 0)
        # 만약 움직일 필요 없다면, (노드의 갯수(count)가 홀수일 때 n == count // 2 + 1일때 발생한다.)
        if offset == 0:
            # 직전 노드의 다음 노드를,
            # 느린 포인터의 다음 노드로 설정한다.
            stack.pop().next = slow.next
            return head

        # 일단 직전 노드를 꺼낸다.
        target = stack.pop()
        # 그리고 offset - 1 만큼 반복해서 앞의 노드를 꺼낸다.
        # 만약 offset이 0이라면 실행되지 않는다.
        for i in range(offset - 1):
            target = stack.pop()
        # 만약 stack이 비어있다면
        if not stack:
            # target이 첫번째 노드가 되고 제거하면 된다.
            return target.next

        # 아니라면 target 노드를 지워준다.
        stack.pop().next = target.next

        return head

음....뭔가 방안2의 코드가 앞의 코드보다 헐씬 더러운 느낌이 드는건...ㅠㅠ 그래도 이 방법으로는 언제나 $n$만큼의 탐색만 하게된다. 문제는 그걸 구현하기 위해 두개의 포인터를 돌리고, 여러가지 조건을 따져야 한다는 점이......정말 좋은건지에 대한 의문이 드는 부분이라는 것...

어차피 이 방법도 시간복잡도로 표현하면 $O(n)$이다. 최악의 경우, $n$이 딱 노드의 갯수와 동일한 상황인데, 이 경우 느린 포인터가 딱 중간점까지 갔다가 다시 첫번째 노드까지 돌아가야 하기 때문이다. 그러니 큰 수의 기준으로는 둘다 비슷한 속도로 돈다는 의미인데, 구현 난이도는 헐씬 복잡하다는 것이...물론 리팩토링을 더 해볼 여지가 없는건 아닌데 지금은 그럴 시간이 없다(...)

끝

Grind 75를 169 전체문제로 돌리고 있는데, 확실히 LeetCode와 BOJ는 촉감이 많이 다르다. BOJ는 약간 시험을 대비해서 열심히 담금질 하는 과정 같다면, LeetCode는 면접을 대비해 여러가지 방법으로 설계하려는데 초점이 있는것 처럼? 아니면 지금 이 문제집이 그런 느낌일지도 모르겠다.

결론은 뭔가 조금 아쉽지만, 어쨋든 원래 알고 있던 알고리즘을 전혀 다른 문제에 적용해 보고, 성공했다는 점에서는 나름 보람찬다. 다만 실제 시험이었다면 적용하지 못했을것이, 실제로 두번째 방안을 구현하는데는 평소 문제 푸는 것보다 헐씬 오래 걸렸다. 아마 시간제한이 있었다면 처음의 두번 반복하는 걸로 시작한 다음 첫번째 방법을 시간이 남으면 생각하지 않았을까 싶다.

아무튼! BOJ는 쉬운 문제로 스트릭만 유지하면서 휴식중이지만, LeetCode에서는 일주일 7~9 문제 정도로 여전히 달리는 중이다. 169 중 유료 구독 필요한 문제 제외하고 다 끝나면 다시 BOJ로 돌아갈지도. 다른 알고리즘 공부하는 분들도, 한번씩 다른 사이트에서 문제 풀어보자. 나름 재밌는 경험을 할지도 모른다.