Hash함수의 사용용도
Hash함수는 암호학 분야에서만 사용하는 것은 아니다.
DB나 다양한 분야에서 사용되었다.
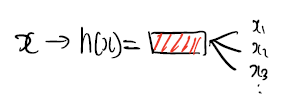
위와 같은 형태로 긴 길이에 대한 정보를 Hash에 넣으면 고정길이의 값이 나와 이를 통해 간단하게 검색할 수 있다.
그러나 이와 반대로 암호학적인 Hash는 아래와 같다.
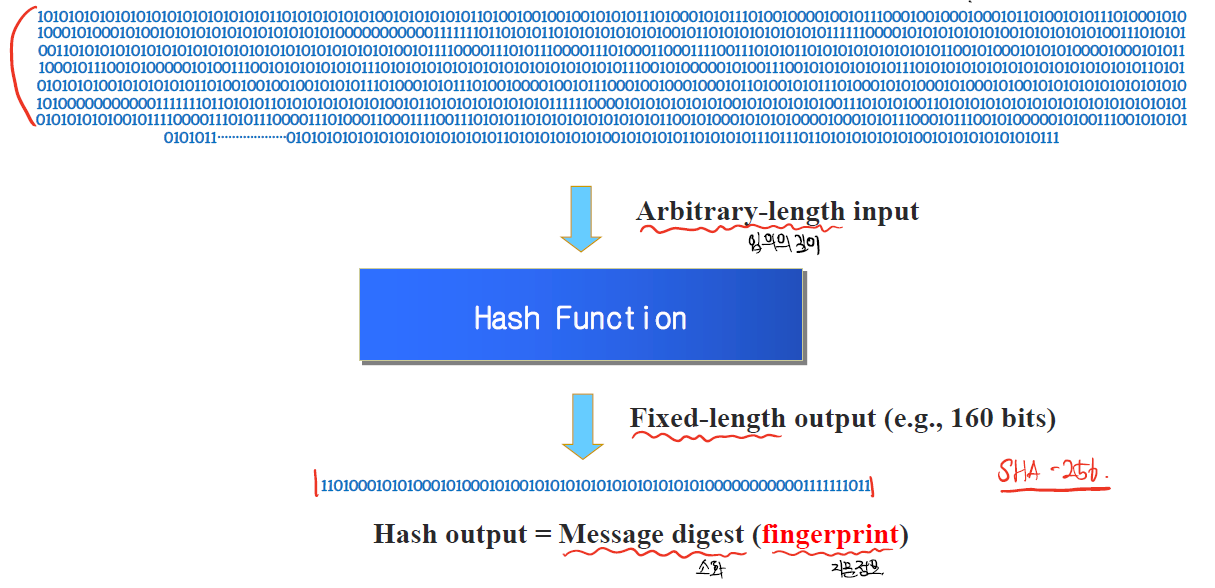
암호학적인 Hash는 input의 길이는 상관없지만 output은 고정되어있다.
이러한 구조를 가질 수 있는 이유는
- 충돌저항성을 가져야한다.(collision resisteance)
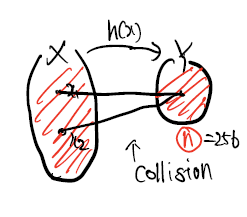
그림에서 보다 싶이 이론적으로는 collision을 피할 수는 없다.
그러나 이는 다항식 시간내에 답을 구할 수 없이 즉 오래걸리는 infeasible합니다.(2의 128승을 계산해야하므로) - Uniformly distributed
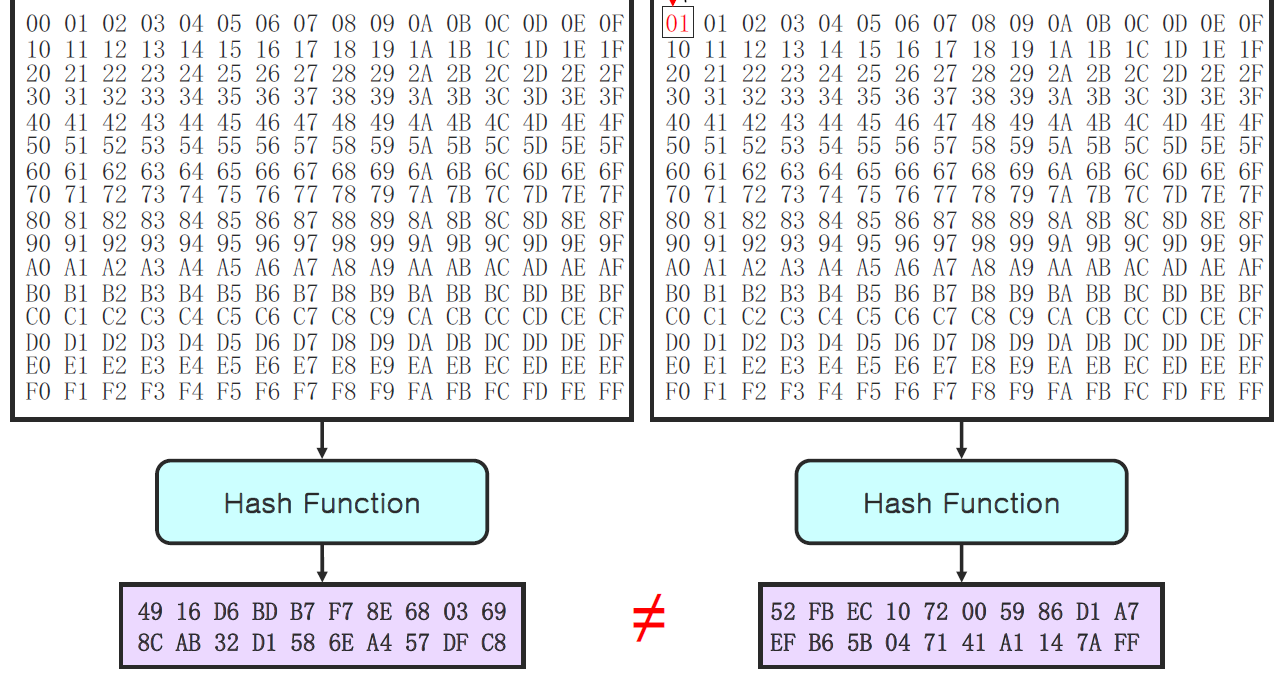
좌우는 거의 같지만 처음의 1bit만 차이가 나는 모습을 보이지만 이를 Hash에 넣을 경우 나오는 값은 모두 같은 확률을 지니는 복원추출과 같은 방식으로 진행되어 값이 틀어지게 된다.
암호학적 Hash를 적용할 수 있는 방법은?
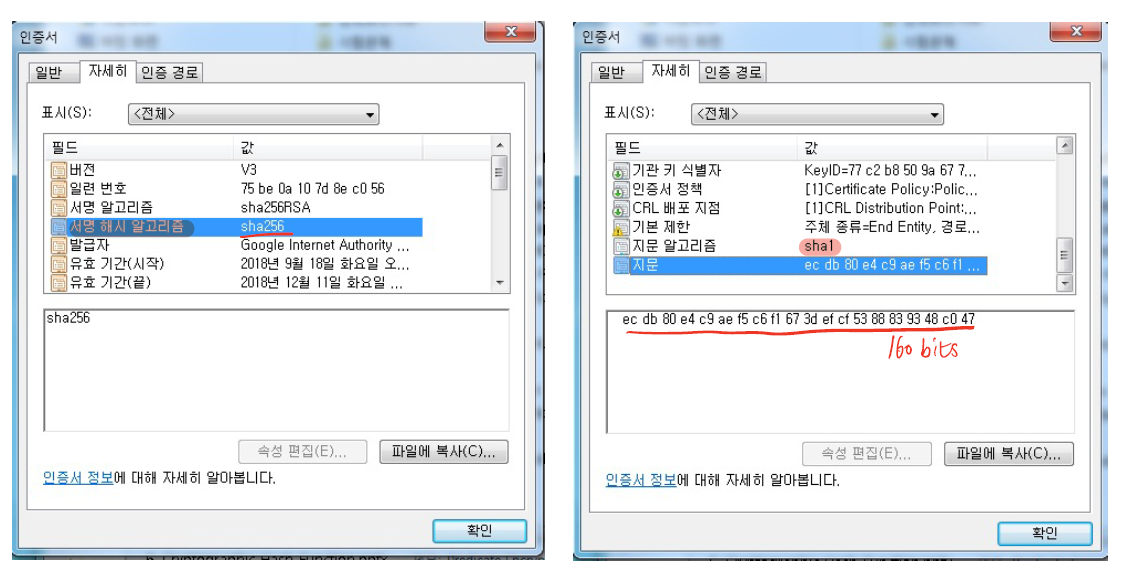
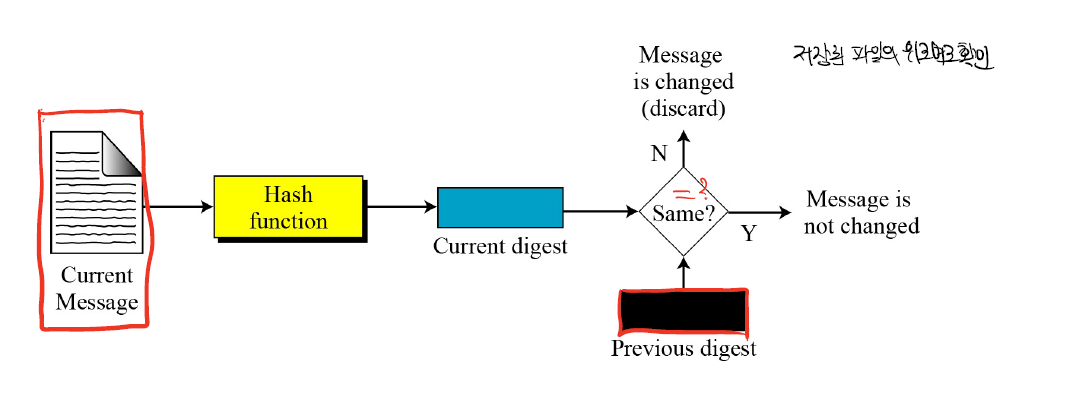
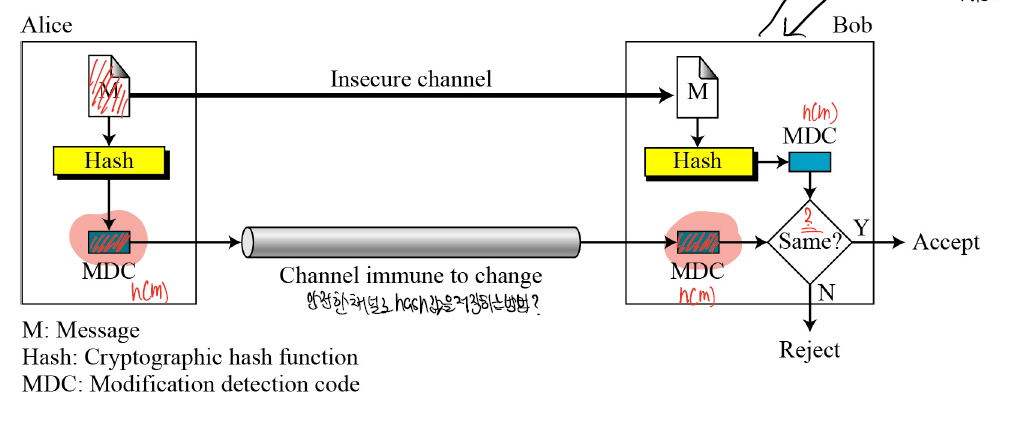
- 파일의 위변조 확인
(문서에 대한 Hash를 취하면 이는 문서의 지문과 같은 역할을 한다.)
암호학적으로 안전한 Hash함수를 가질렴면 다음의 성질이 만족되어야 한다.
- (uniformly distributed)
- Pre-image resistance (one waynewss)
- Second Pre-image resistence
- Collision resistence
- Pre-image Resistence
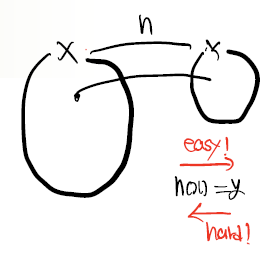
Pre-image resistence는 onewayness라고 말하며 쉽게 말한다면 h(x)= y는 구하기 쉬우나 y-> x를 구하는 것이 어려워야함을 말한다.
이는 실제 OTP에서 사용이 된다.
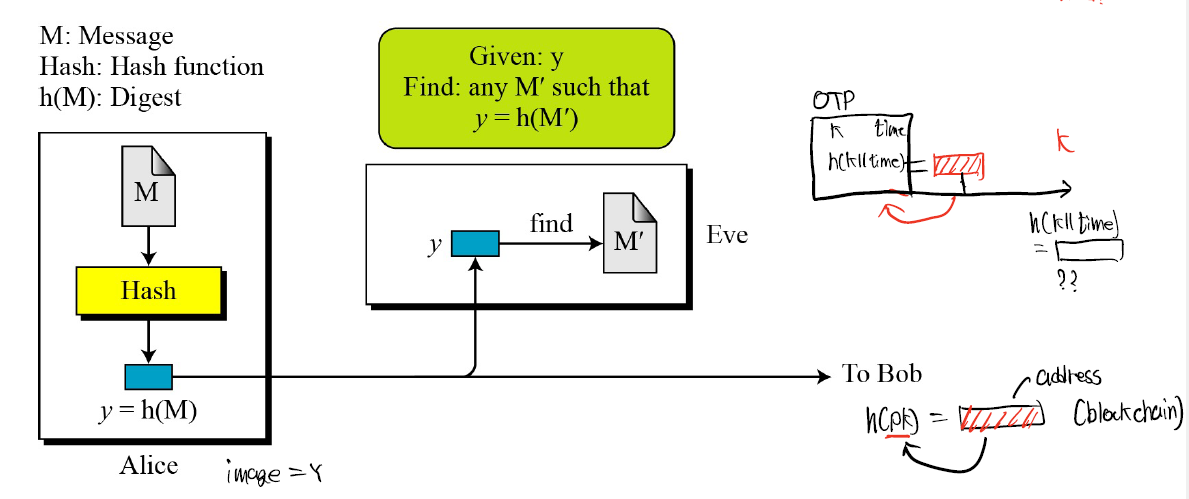
- Second Pre-image Resistence
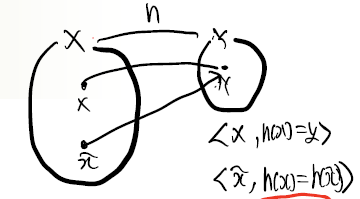
그림과 같이 x와 같은 y값을 가지는 x'을 구할 수 있냐를 말하는 것이다.
실제 시나리오
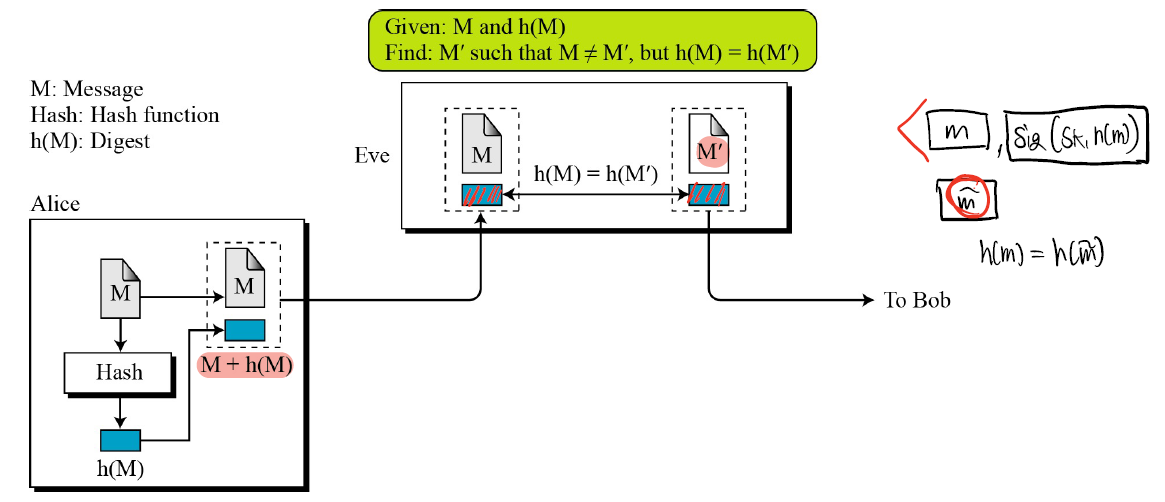
와 같이 위조를 할 수 있다면 ALice에게 불이익인 메시지를 Alice인척 전송할 수 있다는 것이지만 이는 힘들다. - Collision Resistence
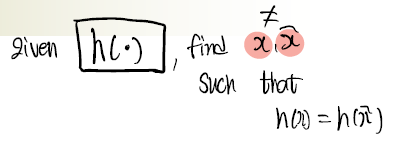
위의 사진과 같이 충돌저항성이다.
말그대로 Hash함수를 주고 x, x'의 충돌쌍을 찾을 수 있냐는 말이다.
실제 시나리오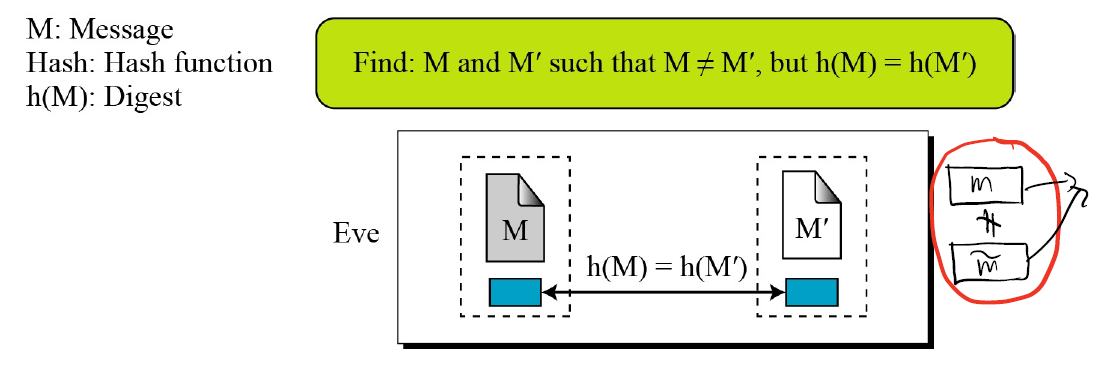
그러나 이 3가지 사이에는 연관관계가 있다.

따라서 Collision resistence함을 만족하면 나머지는 알아서 만족한다는 것이다.
이에 대한 증명에 설명은 따로하지 않고 넘어갈 것이다.
이에 대한 증명들은 reduction을 통해 증명을 한다.
이러한 hash함수들이 안전한지 확인하기 위해
"A Generic ‘Birthday’ Attack"을 통해 얼마정도 충돌저항성을 가지는 지알 수 있다.
이를 통해 나오는 것은 Giving a minimal bound of output length에 따라 어려움이 결정됨을 알 수 있다.
우리가 Hash의 함수를 분석하기 위해 Random Function을 분석한다.
이유는 Hash함수가 닮고 싶어 하는 이상적인 목표가 Random 함수이므로 이를 통해 분석하고 이보다 Hash함수가 성능이 떨어지는 것으로 판단한다.
이를 통해 설계하고 분석하고 취약점을 보완하는 방법으로 구성한다.
이러한 분석을 할 수 있는 Birthday 문제는 따로 언급하지 않을 것이다.
간단히 이야기하면 1.pre-image 2.second pre-image 3.collision에 대한 모델링을 하고 이를 분석하는 방법이다.
과거의 Hash함수들(모두 깨졌다)
MD5 (with digest of 128 bits)
- Which was one of the standard hash functions for a long time
- To launch a collision attack, adversary needs to test 264 (2128/2) tests
- Even if adversary can perform 230 tests in a second, it takes 234 seconds (more than 500 years) - based on the random function
- It has been proved that MD5 can be attacked on much less than 264 tests (in minutes) because of the structure of the algorithm
SHA-1 (with digest of 160 bits)
- Which was one of the standard hash functions developed by NIST
- To launch a collision attack, adversary needs to test 2160/2 = 280 tests
- Even if adversary can perform 230 tests in a second, it takes 250 seconds (more than ten thousand years) – based on the random function
- In 2005, Chinese researchers have discovered that SHA-1 requires time 269 (still theoretically) , which is in less time than 280n Currently, move towards SHA-2 family (SHA-256, SHA-512) and new design(Kecak)
Hash함수의 설계 원리
-
기본적으로 Merkle-Damgard transform을 따르고 있다.
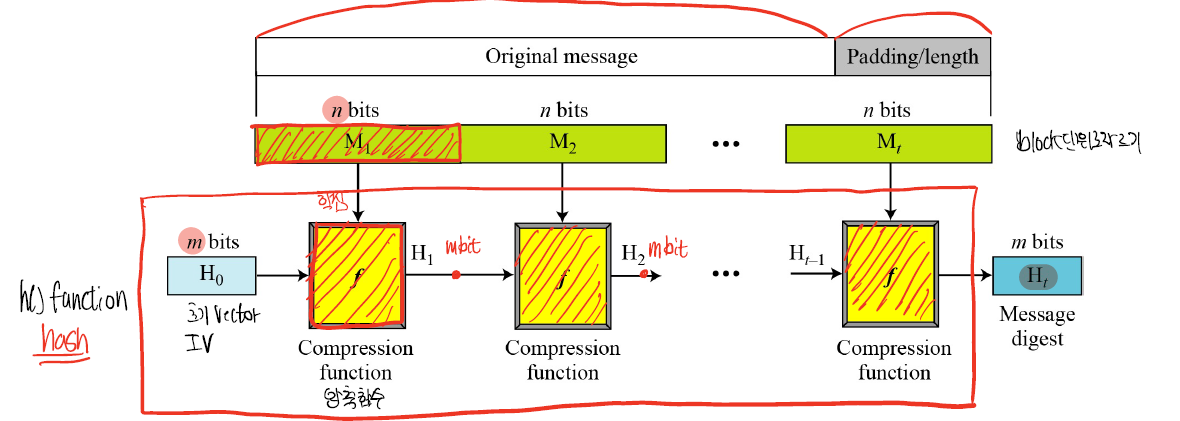
nbit의 block단위로 잘라 이를 압축함수인 f를 통해 mbit를 만들고 이를 다음 block의 IV처럼 f에 넣어 모든 메시지에 대해 수행하면 값이 나온다.
현재의 모든 SHA는 다음의 Spec을 가지고 있다.
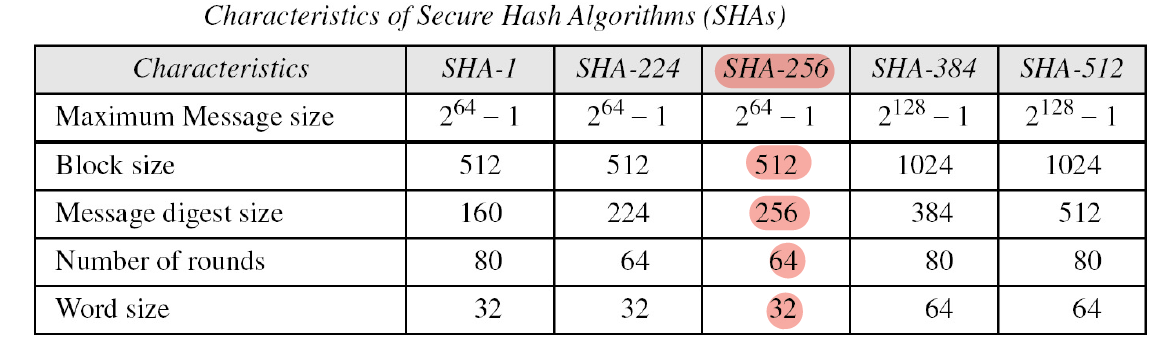
-
Block Cipher기반의 설계
이는 AES함수를 통해 만드는 것이다.
그러나 이는 역방향으로 가지 못하게 즉 invertible하지 못하게 XOR을 하는 방법을 가진다.
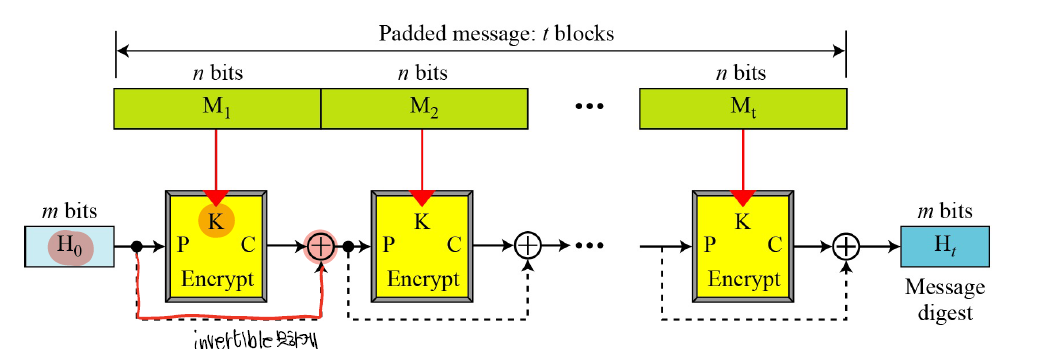
장점은 코드의 size가 줄어든다.
단점은 Hash도 그렇게 코드가 크지않다.
또 다른 방법들
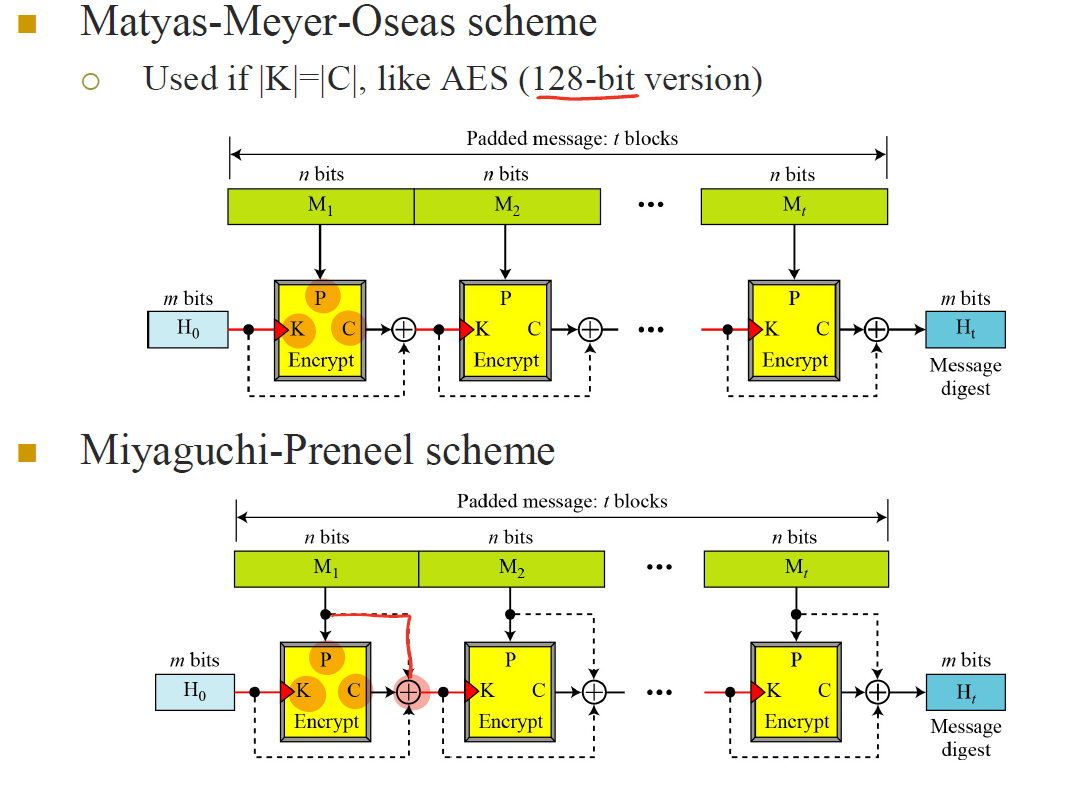
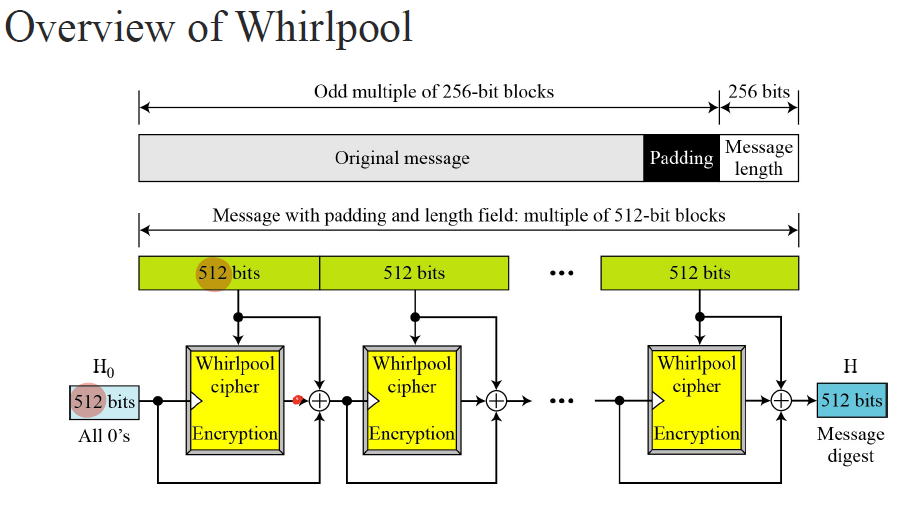
SHA-512
기본적으로 SHA-512는 Merkle-Damgard의 tech를 사용하고 있기에 아래와 같은 구조를 띈다.
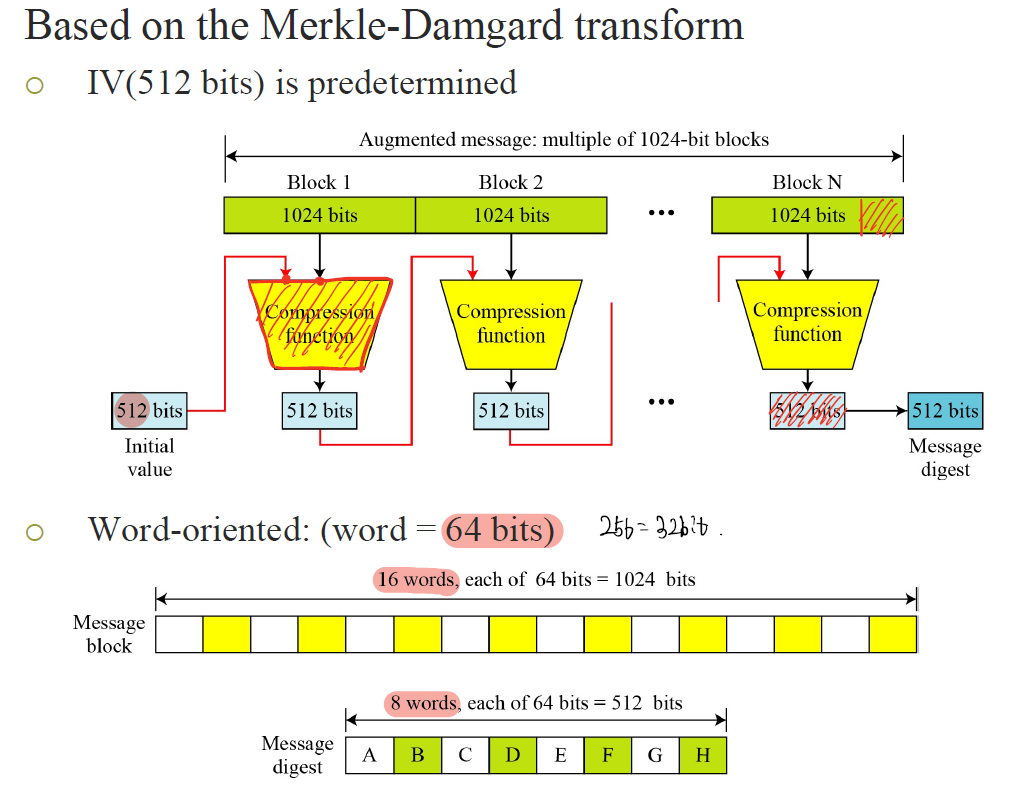
여기서 word단위는 64bits 이다
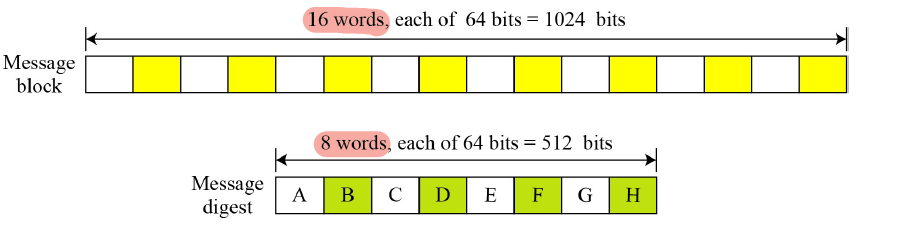
그리고 앞에서 말했다 싶이 메시지가 들어올때 메시지의 길이를 맞추기 위해 padding을 진행한다.
Padding을 하는 방법은 아래와 같다.
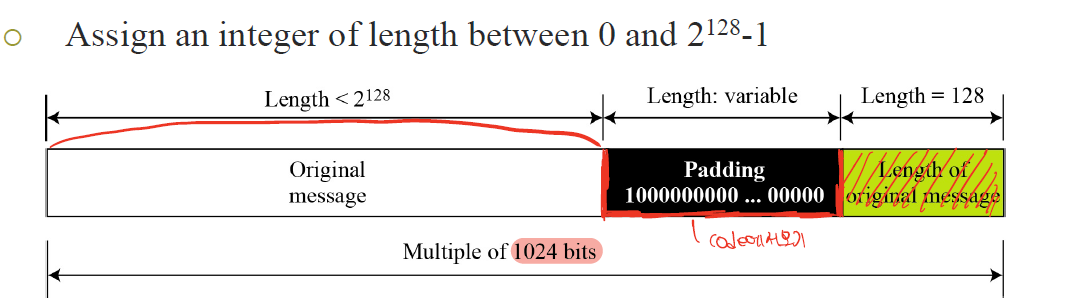
그리고 추가적으로 초기 vector가 필요하므로 아래와 같이 구성이 된다.
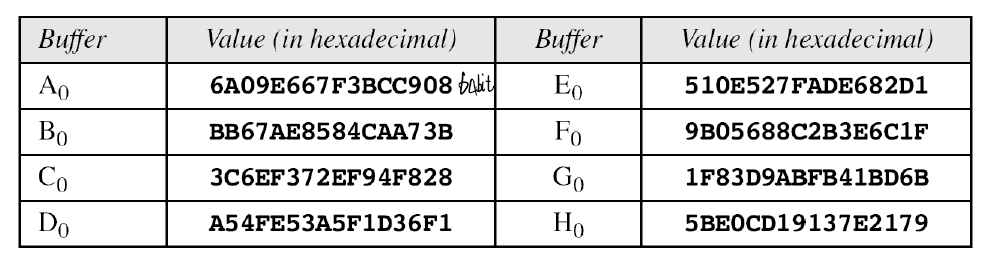
압축함수의 구조
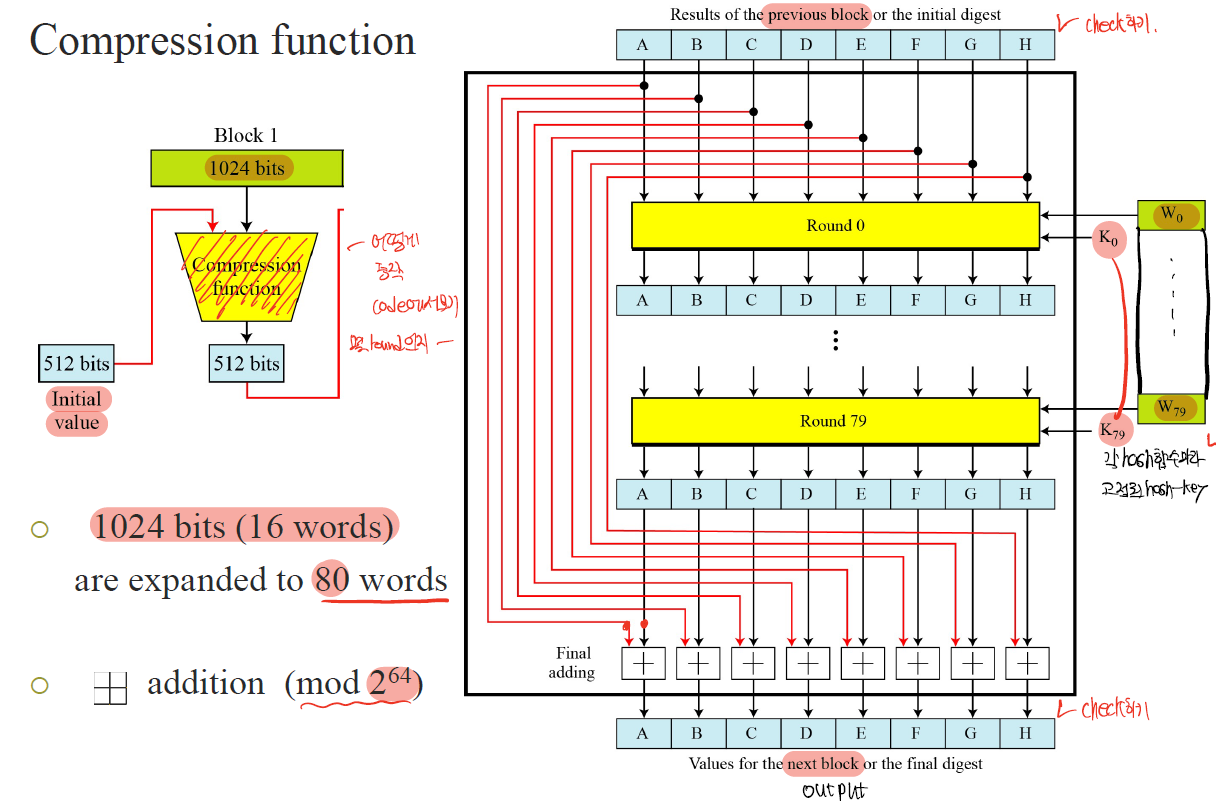
Word expansion
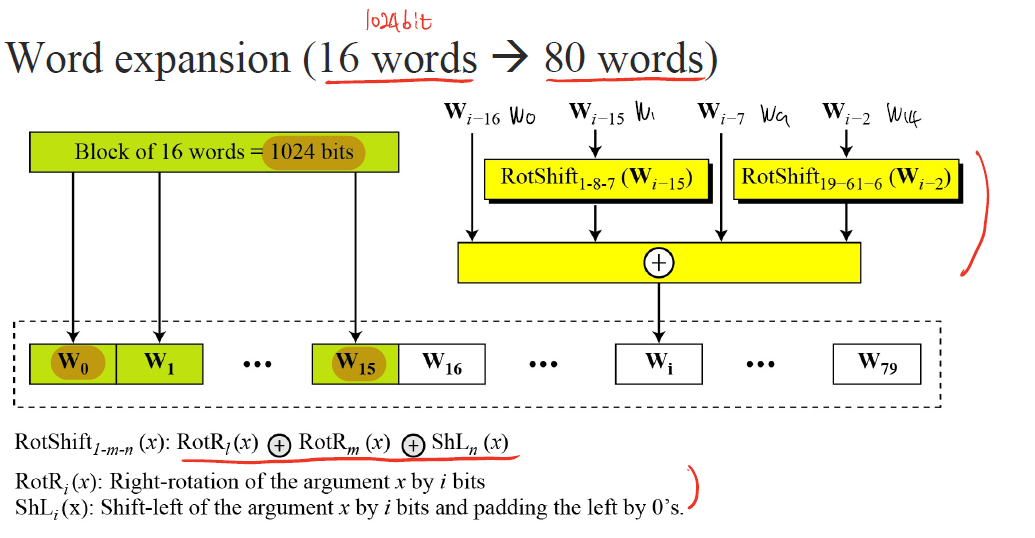
Round function
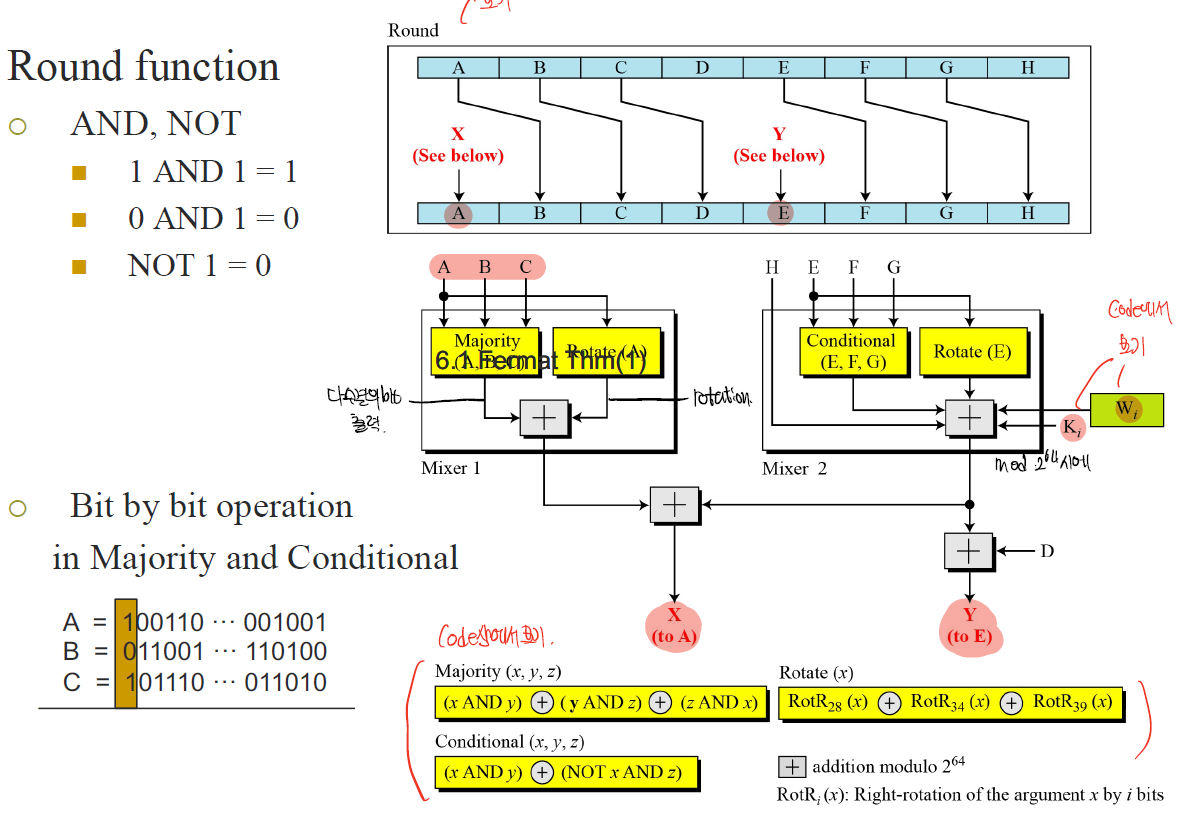
Hash함수의 활용
- Digital signatures(전자서명)
- Public key encryption systems
KDF(Key Derivation Function)
1.Pw-> H(Pw)
2.Cert - Message authentication code (MAC)
1. File
2. public Message
3. Public File(update)

- Applications where pseudo-randomness is required
1. Span Reduction
2. bitcoin
