이전에 배웠던 것은 ~
이전에 배웠던 것은 대칭키 암호로 이는 실제 사용하기에 많은 문제가 발생한다.
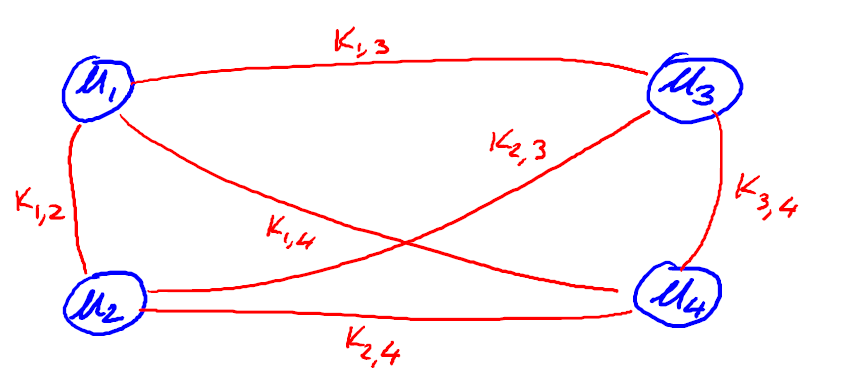
해당 그림에서 보다 싶이 모든 사람들이 대칭키를 통해 통신을 하기 위해선
각각의 n명의 유저들이 n-1개의 key를 공유하고 있어야한다는 문제가 있다.
이를 해결하기 위한 방법은?
- TTP(Online Trusted Thread Party)를 둔다.
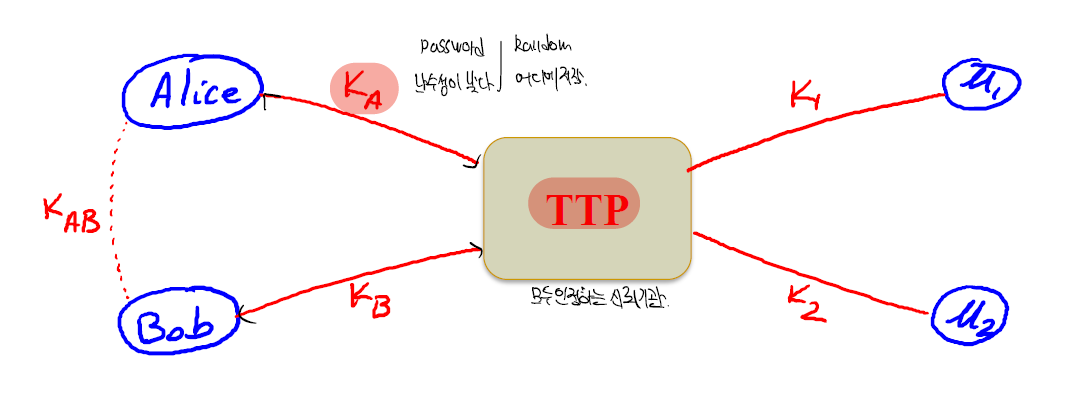
말 그대로 모든 사용자가 신뢰하는 기관을 두고 이 기관이 key 분배에 관여하여 모든 사용자들이 TTP에게만 key를 공유하여 다른이들과 통신한다.
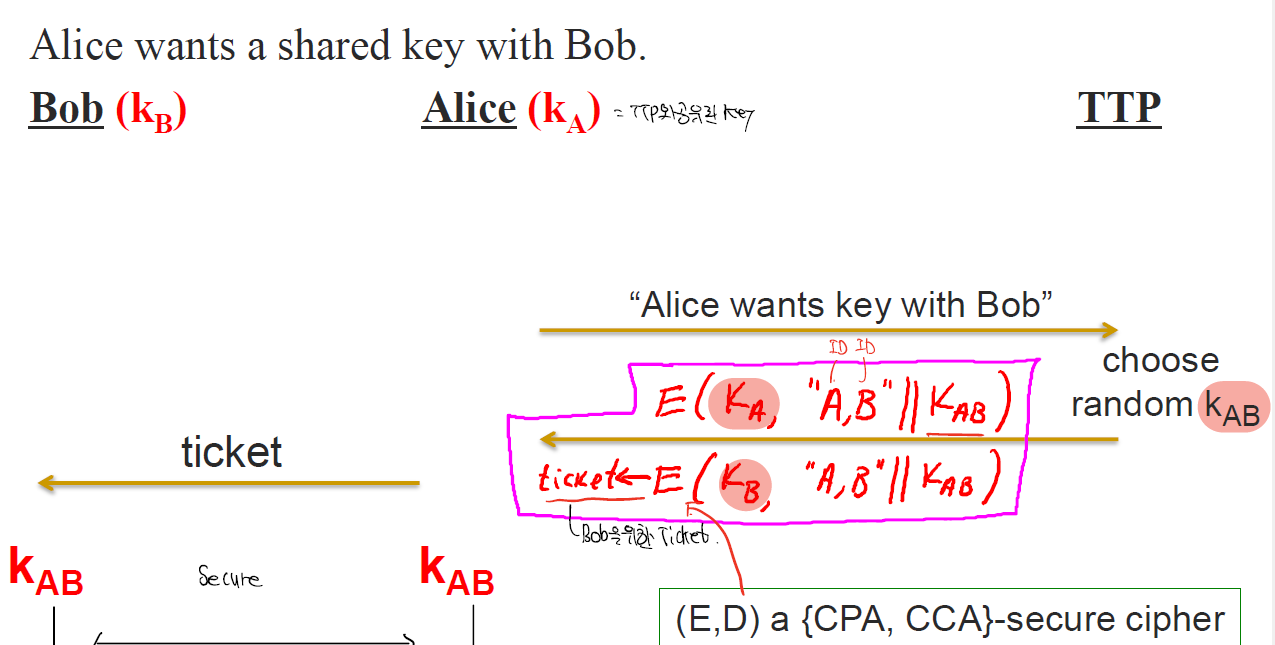
위의 사진과 같은 통신이 이뤄지는데
but 그러나
이는 아래의 문제점을 가진다.
- 신뢰할 수 있는 TTP가 존재해야한다.
- 각각의 사용자가TTP와 적어도 1번 통신해야한다.
- TTP는 모든 사용자들의 통신을 볼 수 있다.(Big brother)
이를 해결하기 위한 방법이 무엇일까?
2. Public-key cryptography
4가지의 방법이 있다.
- Diffie-Hellman (1976)
- RSA (1977), ElGamel (1979)
- ID-based enc (BF 2001)
- Functional enc. (BSW 2011)
이러한 공개key암호기법의 개념을 이야기한 것이 바로 “New Directions in Cryptography”이고 이는 1976년에 Diffie and Hellman 이야기했다.
이에 대한 개념은 다음과 같이 생각하면된다.
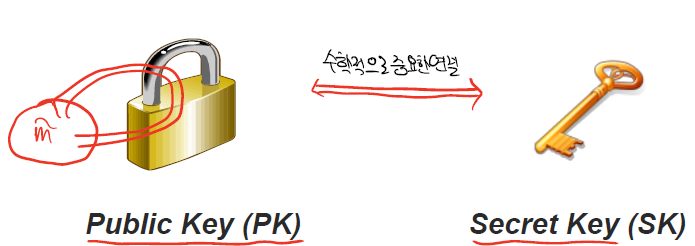
아래와 같은 형식으로 2가지 key인 PK, Sk가 있고 PK는 자물쇠로 평문을 암호화 하는 key이고 SK는 자물쇠의 열쇠로 암호문을 평문으로 바꿔주는 key이다.
Public-Key Encryption (PKE)
3가지의 알고리즘으로 구성되어있다.
1. Gen(i)
2. Enc(PK, m)
3. Dec(SK, CT)
이 있고 이들은 아래와 같이 진행된다.
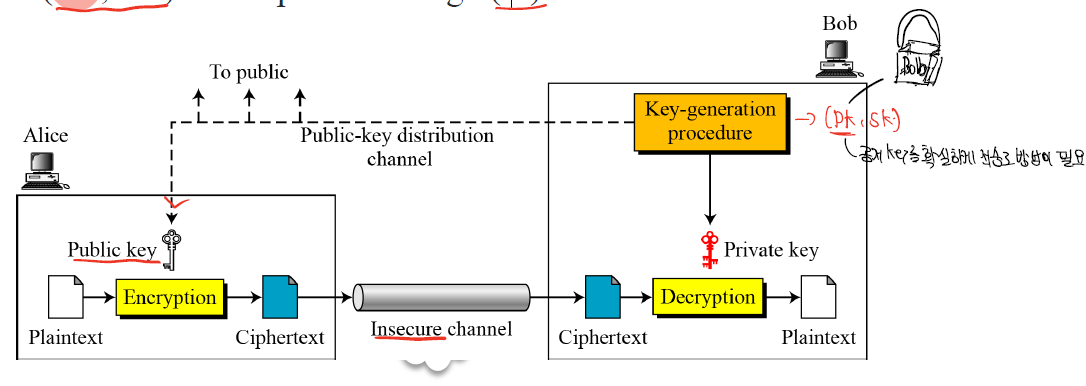
Alice가 bob의 Pk를 가지고 이를 평문을 암호화해서 이를 bob에게 전달하면 bob은 SK를 통해 평문을 해독한다.
그러나 bob의 Pk가 bob의 소유임을 확인하는 것이 필요하다.
이것이 없다면 pk를 바꿔치기하여 공격을 진행할 수 있다.
Security of PKE
공격자는 Pk를 이미 가지고 있다.
그리고 공격자는 CPA 공격자라고 생각했을 경우 아래와 같이 진행된다.
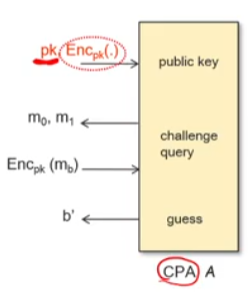
공격자가 메시지(m)을 내보내면 받은이는 공격자가 준 암호문과 임의로 작성한 암호문을 임의로 공격자에게 주고 이를 공격자가 어떠한 것에서 왔는지 맞추는 확률이 1/2정도라면 이는 CPA에 안전하다는 것이다.
즉 C'가 M에 대한 정보를 노출하지 않는다라는 의미이다.
실제 응용에서 사용하는 방식
- HTTPS
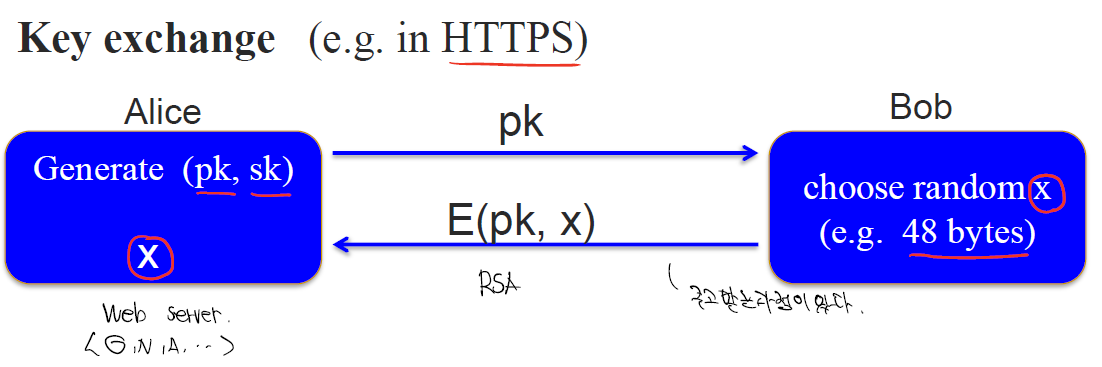
공개key암호를 통해 key-exchange를 해결하고 하위의 통신에서 이 key를 하지고 안전하게 통신하는 것이다. - PGP(Email)
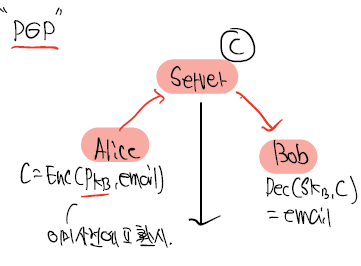
위으 Https는 interactive하게 동작하지만 email은 interactive하지 않게 동작한다.
위의 그림에서 보다싶이 Alice가 bob의 Pk를 통해 암호문을 전송하는고 bob은 Sk로 복호화한다.
그리고 PGP는 미리 보내는 이의 Pk를 받아온다.
그렇기에 대화형식으로 주고 받지 않아 non-interactive하다. - Secure Cloud Service
클라우드 서비스에 올라가는 자료는 암호화해서 이를 주고 받지만 문제는 클라우드 서버는 이러한 자료들에 대한 key를 가지고 있기에 클라우드 서버는 모두 볼 수 있다.
그렇기에 이러한 클라우드 서버의 문제를 해결하고자 파일자체를 암호화해서 올리는 방법을 고안했다.
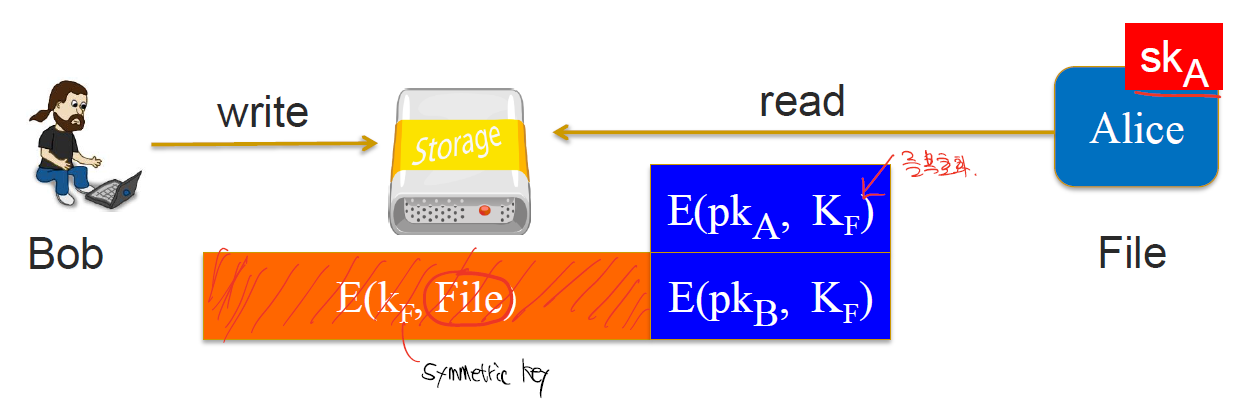
위의 그림과 같이 대칭키를 사용해서 파일을 암호화하고 이 대칭키를 공개키로 암호화 해서 header에 붙인다.
따라서 이러한 header를 복호화 할 수 있는 방법은 Pk에 대한정보를 미리 구성하지 않는한 파일을 복호화 할 수 없다.
Key Exchange
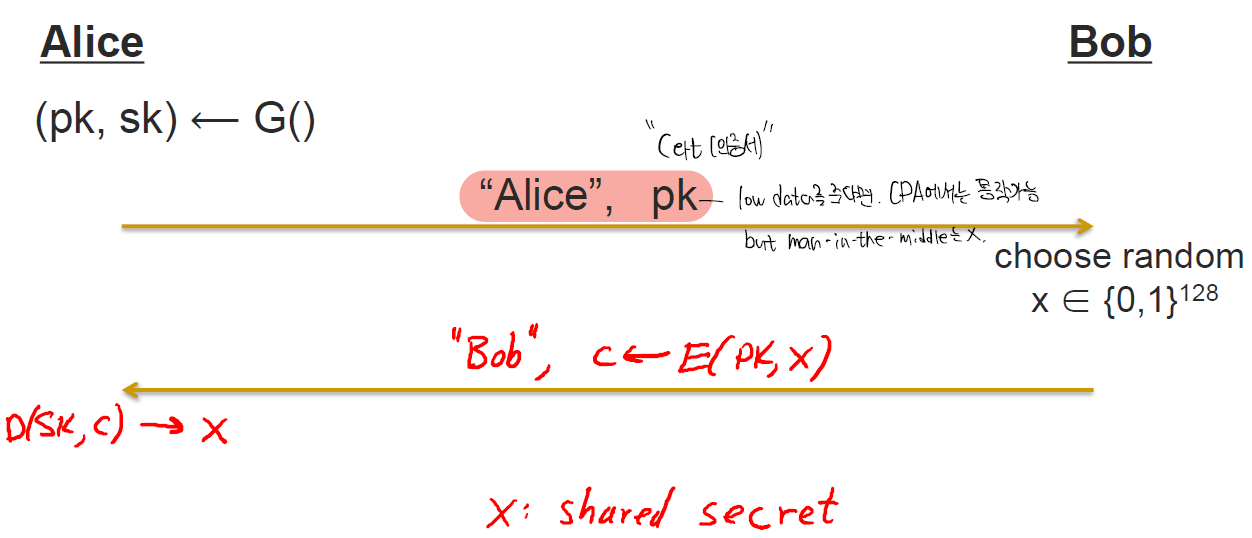
위의 방식으로 키를 교환한다.
CPA에 대한 공격자는 CPA에 대한 암호로 보완할 수 있지만
이러한 공격은 Man-in-the-middle attack에 문제가 발생한다.
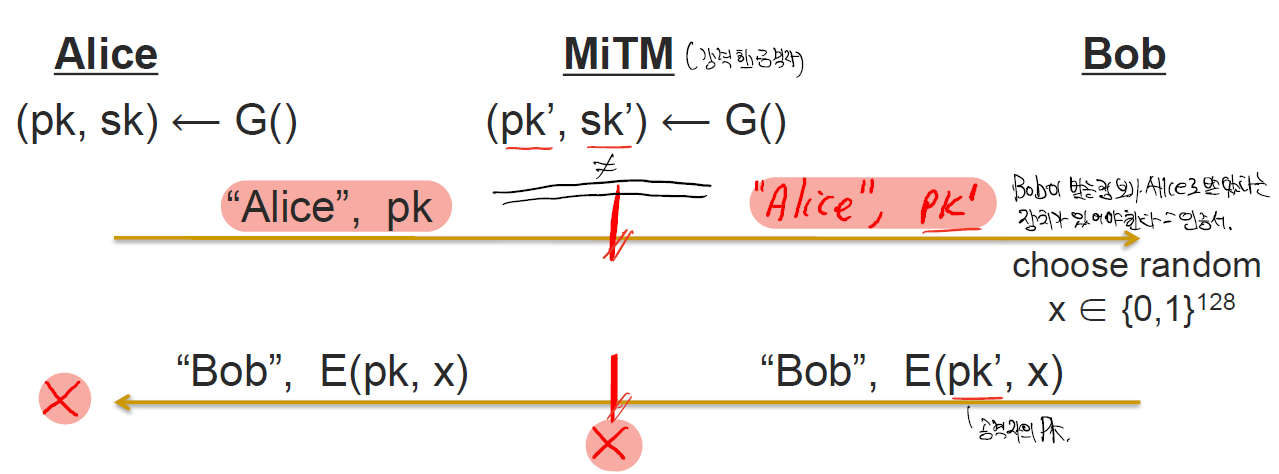
위의 그림에서 보다 싶이 중간에 강한 공격자가 pk,sk를 바꿔치기 한다면 두사람의 통신에는 문제가 없으나 공격자는 둘의 통신을 모두 감청할 수 있다.
이 공격에서 가장 중요한 것은 원래 Alice가 보낸것과 bob이 받은 것이 다르다.
따라서 이러한 것이 위변조 되지않았는지를 확인할 수 있는 인증서(cert)가 필요하다.
만약 긴 메시지를 암호화 하고자 한다면
이전의 방식처럼 잘라서 하는 것이 아닌 다음과 같은 방식을 사용한다.
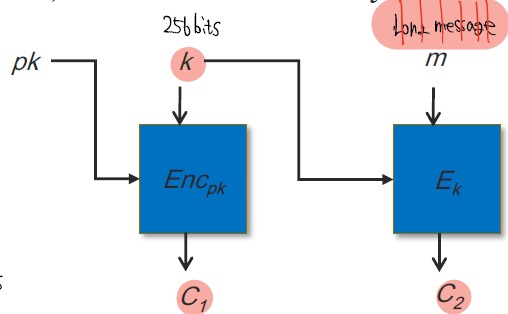
- Hybrid encryption (= PKE+SKE)
두가지를 섞어서 긴 메시지를 처리한다.
이 과정은 아래의 그림처럼 동작한다.

RSA Encryption

이 방식은 이전의 방식고 달리 소인수 분해의 어려움을 이용한 방식이다.
따라서 이는 mod연산과 지수연산을 통해 작동한다.
따라서 다음과 같이 Pk, Sk가 구성된다.
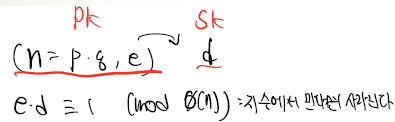
그리고 이러한 key들을 통해 이전에 배웠던 것고 비슷하게 동작하지만 이는 mod연산과 지수연산을 통해 평문을 암호화하고 key를 통해 또 역시 mod연산과 지수연산을 통해 평문을 복호화 한다.
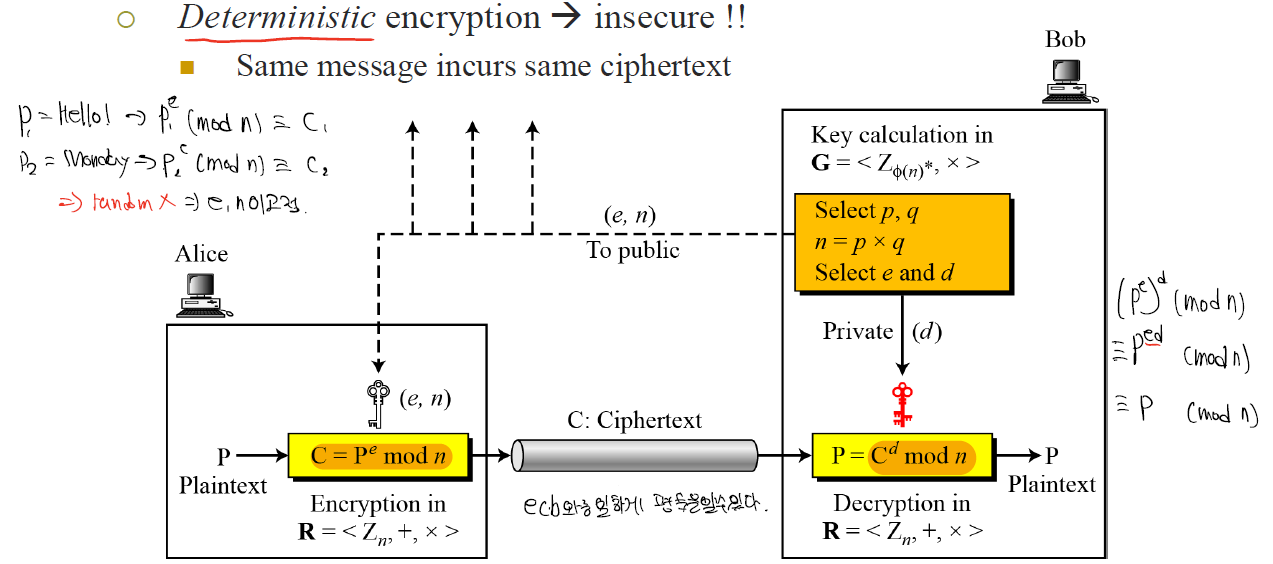
그러나 이러한 RSA의 방식에 는 큰 문제점을 지닌다.
- 동일한 메시지는 같은 암호문이 나온다.
이는 random성을 줄 수 있는 옵션이 없기에 그렇다.
이러한 지수승을 구하는 방법은
Square-and-multiply method을 통해 쉽고 빠르게 계산이 가능하다.
위의 문제를 해결하는 방법
- Padded RSA

이는 Randomize 알고리즘을 통해 이전의 문제점을 해결하였다.
그러나 Random String이 적당히 길어야한다.
그러나 현실은? - PKCS#1 v1.5

위의 사진과 같은 방식으로 Padding을 진행한다.
이 방법은 Https를 할떄 사용하는 방식이다.
이 방법은 CCA에 안전하지 않기에 RSA-OAP가 나왔다. - PKCS#1 v2.0(RSA-OAP)
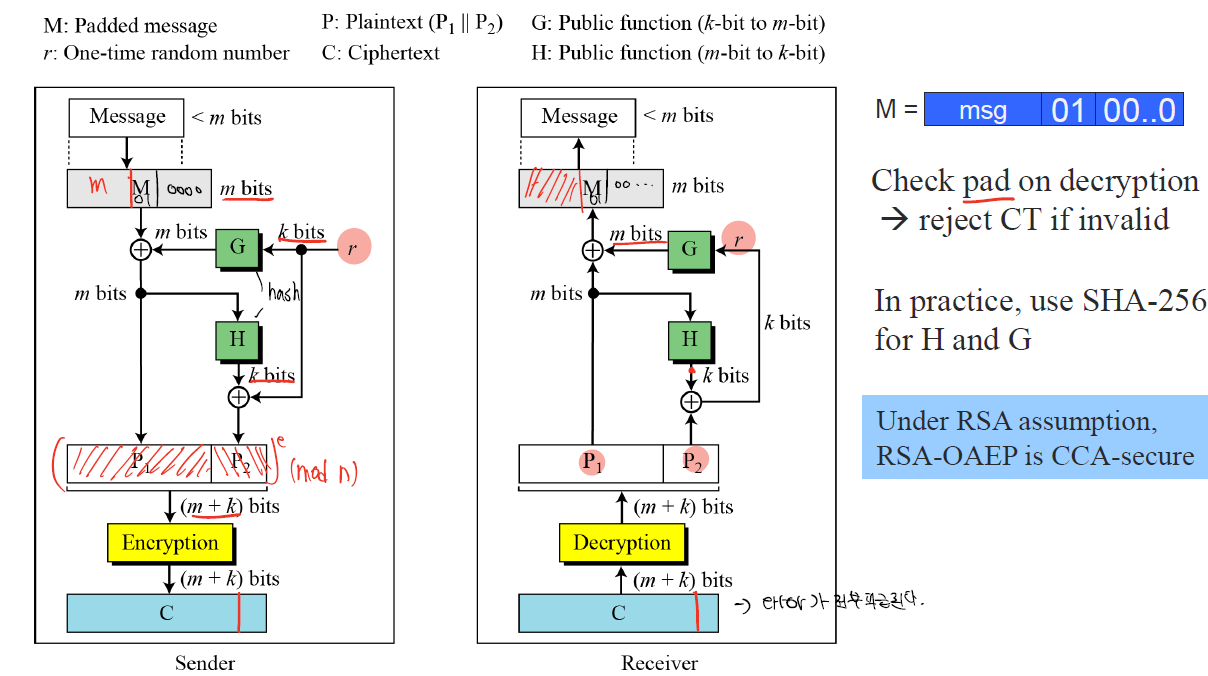
내부의 인코딩 방식이 조금더 변화되었다.
현재 e에 대한 값으로 010001(65537)을 사용한다.
RSA는 암호화에서는 빠르나 복호화는 조금 느리다.
Timing Attack

위의 그림과 같이 계산을 할 때 나오는 point들에서 곱셈이 이뤄질 것이므로 이러한 곳에서 나오는 전자파나 전력등을 측정해서 공격한다.

이런식으로 공격하는 방법이 timing attack이다.
이러한 공격을 막기위해 Dummy연산을 수행하기도 한다.
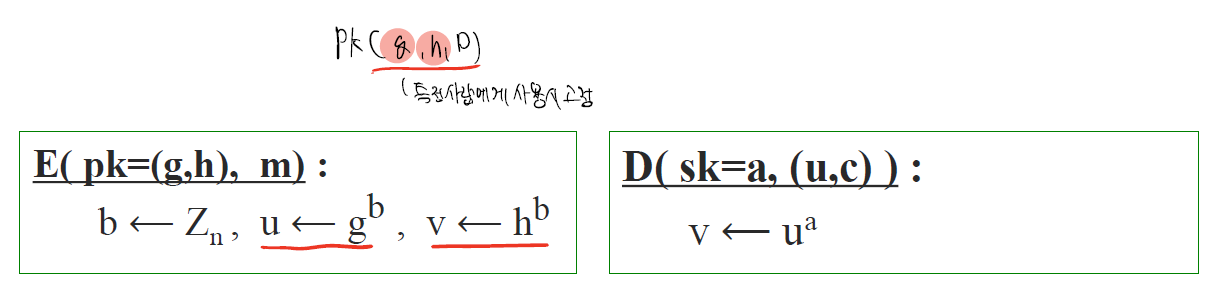
ElGamal Encryption
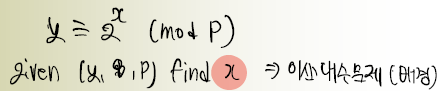
이 역시도 이산대수를 구할 수 있나는 문제이다.
이 문제 역시 x값을 구하기 힘들다.
x를 아는 이만 복호화가 가능하다라는 점에 착안해 아래와 같이 구성하였다.
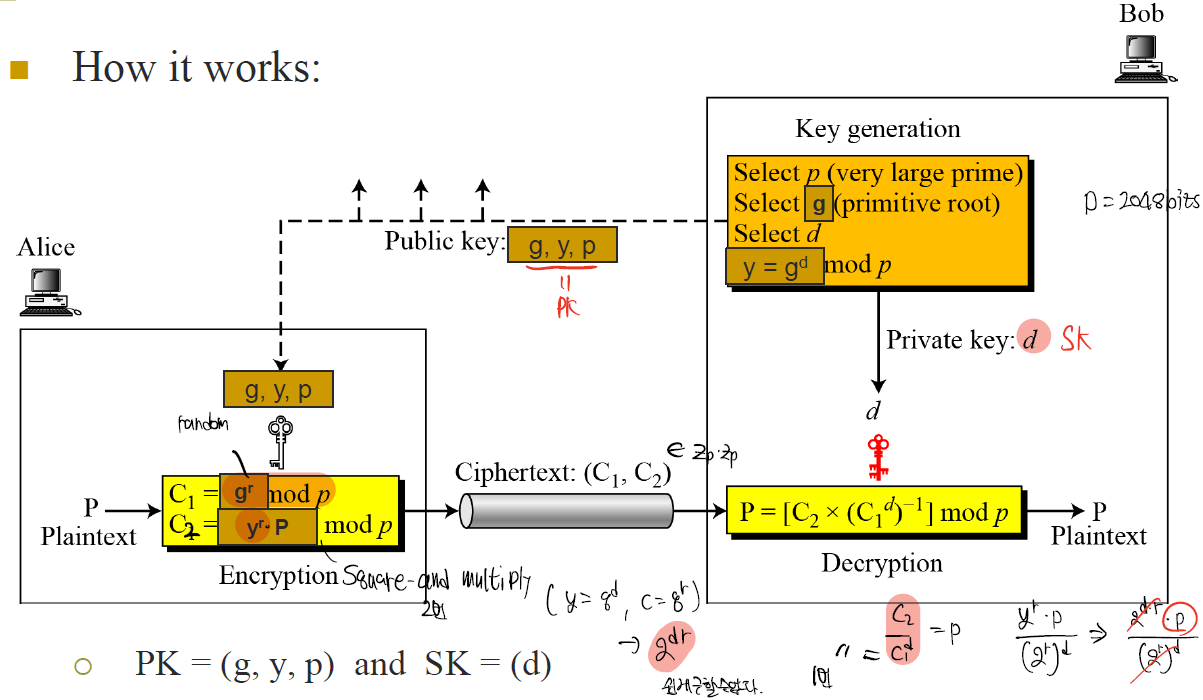
이는 암호화를 할 때 지수승 연산을 2번을 한다.
복호화에서는 1번의 지수승연산이면 된다.
ElGamal의 장점
이전의 RSA는 padding을 통해 Randomize를 진행할 수 있었지만
ElGamal은 이미 Randomize되어있기에 따로 Padding이 필요없다.
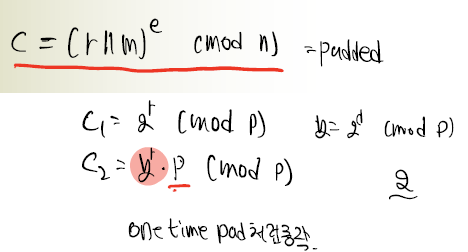
ElGamal Encryption의 안전성
이 안전성 역시 위의 RSA와 동일한 방식으로 진행된다.
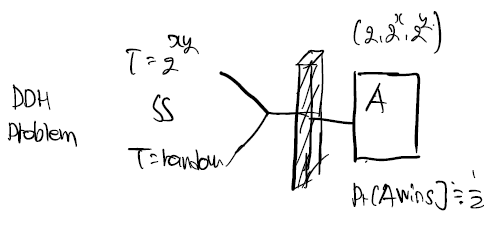
DDH의 문제가 어렵다면 y의 r승은 random처럼 보이기에 one time Pad처럼 동작이 가능하다라는 것을 알 수 있다.
그러나 이러한 방식에 대해 ElGamal을 사용할 의미가 없었다.
RSA도 padding만 잘한다면 이점이 있기에 ElGmal이 사용되지않고 있었다.
ElGamal system (DHIES/ECIES)
이전까지 배웠던 기법들을 비교한다면 아래의 그림과 같이 나온다.
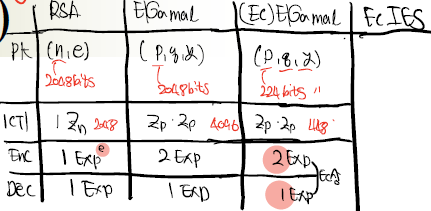
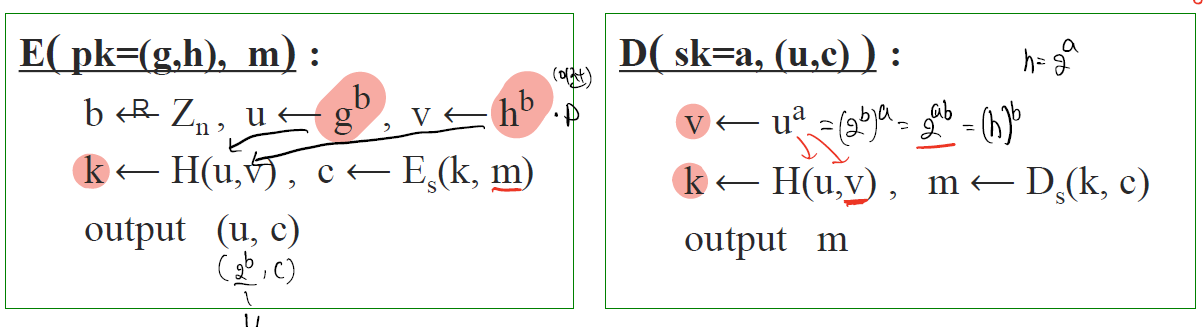
이러한 암호화 복호화를 볼때 ElGmal을 사용할 이유가 없었다.
그러나 위의 사진과 보다싶이 EC(타원곡선)이 등장하면서 상황이 바뀌게 되었다.
p와 g의 크기가 작아지므로 RSA보다 작기에 이는 매우 대단한 이점을 가지게 되어 ECElGmal을 사용하게 되었다.
Fixed Base일 경우에 사전의 계산을 통해 미리 계산을 해 빠르게 수행할 수 있다.
