3Sum

이 포스트에서는 leetcode의 3Sum 문제를 다뤄보도록 하겠다.

• 문제링크: 3Sum
• 솔루션: source code

1. 문제분석

주어진 문제를 간단하게 요약해보면 아래와 같다.

중복된 요소를 허용하는 정수 배열에서 3개의 숫자를 골라서(고른 숫자를 각각 a, b, c라고 하자) a+b+c=0 이되는 triplet을 중복 없이 출력하세요.

2. 가장 멍청한 풀이

섹션의 제목이 '가장 멍청한 풀이' 이기는 하지만 알고리즘을 공부할 때 가장 멍청한 풀이부터 가장 스마트한 풀이까지 사고의 흐름을 정리하는 과정은 매우 중요하다.

따라서, 이 섹션에서 '가장 멍청한 풀이' 에 대해서 꼭 한번 짚고 넘어가고자 한다.

떠올려볼 수 있는 가장 멍청한 풀이는 3중 for-loop을 사용하는 것 정도가 될 수 있을 것 같다.

만약 주어진 정수 배열에 중복이 없었다면, 아래와 같은 3중 for-loop 코드를 뇌의 개입 없이 작성할 수 있다.

vector<vector<int>> threeSum(vector<int>& nums)
{
  vector<vector<int>> ret;

  int len = nums.size();
  for (int pa = 0; pa < len; ++pa) // a를 고르는 loop
  {
    for (int pb = pa + 1; pb < len; ++pb) // b를 고르는 loop
    {
      for (int pc = pb + 1; pc < len; ++pc) // c를 고르는 loop
      {
        int a = nums[pa];
        int b = nums[pb];
        int c = nums[pc];
        if (a + b + c == 0)
        {
          ret.push_back(vector<int>{a, b, c});
        }
      }
    }
  }

  return ret;
}

이제 정수 배열에 있는 중복까지 고려하려면, 어떻게 하면 a/b/c를 고르는 각 루프가 한 번 골랐던 숫자를 2번 이상 고르지 않게할까?와 같은 고민에 직면하게 된다.

고민의 답은 주어지는 정수 배열을 사전에 정렬해두는데에 있다.

주어진 배열이 $given$과 같고, 정렬을 통해 $sorted$를 얻었다고 하자.

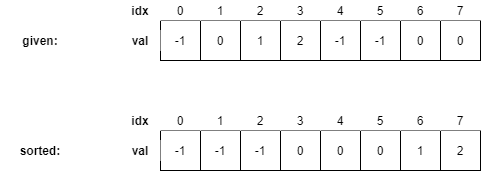
직전에 설명한 중복 없는 정수 배열에 대한 풀이의 첫번째 loop body를 수행할 때 pa, pb, pc의 위치는 아래와 같을 것이다.

두번째로 loop body를 수행할 때 pa, pb, pc의 위치는 아래와 같을 것이다(pc가 한 칸 이동함).

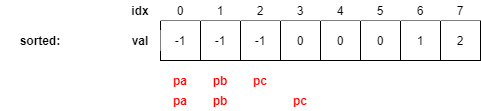
세번째로 loop body를 수행할 때 pc의 이동이 중복을 고려하기 위한 키 아이디어인데, pc는 이미 0을 골라봤으므로 같은 값을 가지는 4,5번째 값은 고르지 않고 6번째 값으로 곧장 이동할 수 있다.

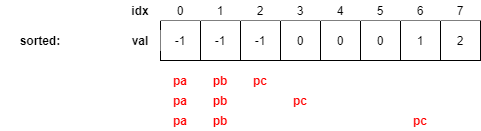
여기까지만 봐도 감이 오겠지만 확실한 설명을 위해 몇 번만 더해보도록 하겠다.

네번째로 loop body를 수행할 때 pc는 건너뛸 중복이 없으므로 그냥 옆으로 한 칸 이동한다.

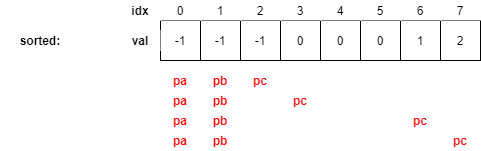
다섯번째 loop body는 pc에 대한 loop이 끝나고, pb가 이동하는 loop이 될 것이다.

상술했던 pc의 움직임과 마찬가지로 pb도 중복된 숫자를 건너뛰고 3번째 값으로 직행한다.

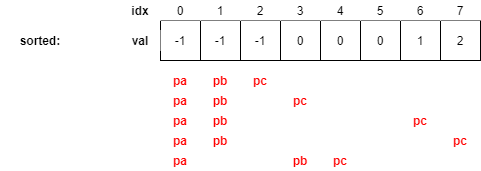
지금까지 이야기한 방법을 코드로 구현하면 아래와 같다.

vector<vector<int>> threeSum(vector<int>& nums)
{
  sort(nums.begin(), nums.end());

  vector<vector<int>> ret;

  int len = nums.size();
  int pa, pb, pc;
  int a, b, c;

  pa = 0;
  while (pa < len)
  {
    a = nums[pa];
    pb = pa + 1;
    while (pb < len)
    {
      b = nums[pb];
      pc = pb + 1;
      while (pc < len)
      {
        c = nums[pc];
        if (a + b + c == 0)
        {
          ret.push_back(vector<int>{a, b, c});
        }

        // Skip 'c's that we choose before
        while(++pc < len && nums[pc] == c)
        {
        }
      }
      // Skip 'b's that we choose before
      while(++pb < len && nums[pb] == b)
      {
      }
    }
    // Skip 'a's that we choose before
    while(++pa < len && nums[pa] == a)
    {
    }
  }

  return ret;
}

알고리즘의 복잡도는 주어진 배열의 길이를 $n$이라고 할 때, 정렬에 $O(nlogn)$, 3중 while-loop에 $O(n^3)$이므로 총 $O(n^3)$이 된다.
이대로 제출하면 당연히 TLE를 맞는다.

3. 적당히 똑똑한 풀이

이제 적당히 똑똑한 풀이(적어도 TLE는 나지 않는)를 알아보도록 하자.

기본적인 풀이의 틀은 섹션 2에서와 크게 다르지 않은데, 우리는 섹션 2에서 중복을 헤아리기 위해 주어진 배열을 정렬했다.

배열을 정렬했다는 것은 곳 bsearch와 같은 $O(logn)$ 류 알고리즘들을 쓸 수 있게된다는 것을 의미한다.

따라서, 적당히 똑똑한 풀이에서는 pa, pb를 통해 a, b를 고르고 nums[pb+1:len]에 c=-a-b인 c가 존재하는지를 bsearch로 검색해준다.

기본적은 풀이의 틀이 섹션 2와 크게 다르지 않으므로 바로 코드를 보이도록 하겠다.

/**
 * @brief Find 'target' from sorted vector 'sorted_nums' starting at 'begin' and ending at 'end-1'
 * 
 * @param sorted_nums Sorted integer vector
 * @param begin Range to be searched(closed)
 * @param end Range to be serached(opened)
 * @param target Target value
 * @return int -1 when not existing, index of target value otherwise
 */
int bsearch(vector<int> &sorted_nums, int begin, int end, int target)
{
  int lo = begin;
  int hi = end - 1;

  while (lo <= hi)
  {
    int mid = (lo + hi) / 2;
    if (sorted_nums[mid] < target)
    {
      lo = mid + 1;
    }
    else if (sorted_nums[mid] > target)
    {
      hi = mid - 1;
    }
    else
    {
      return mid;
    }
  }

  return -1;
}

vector<vector<int>> threeSum(vector<int> &nums)
{
  sort(nums.begin(), nums.end());

  vector<vector<int>> ret;

  int len = nums.size();
  int pa, pb, pc;
  int a, b, c;

  pa = 0;
  while (pa < len)
  {
    a = nums[pa];
    pb = pa + 1;
    while (pb < len)
    {
      b = nums[pb];
      pc = pb + 1;

      pc = bsearch(nums, pc, len, -a - b);
      if (pc != -1)
      {
        c = nums[pc];
        ret.push_back(vector<int>{a, b, c});
      }

      // Skip 'b's that we choose before
      while (++pb < len && nums[pb] == b)
      {
      }
    }
    // Skip 'a's that we choose before
    while (++pa < len && nums[pa] == a)
    {
    }
  }

  return ret;
}

알고리즘의 복잡도는 주어진 배열의 길이를 $n$이라고 할 때, 정렬에 $O(nlogn)$, a, b를 골라 c를 bsearch하는데 $O(n^2logn)$이므로 총 $O(n^2logn)$이 된다.

이렇게 풀면 적어도 Accept은 받을 수 있거, 백분위가 22% 정도 되는 것 같다.

4. 조금 더 똑똑한 풀이

이번에는 조금 더 똑똑한 풀이를 알아보자.

여기에서는 pa를 통해 a를 고른 뒤에 b+c=-a가 되는 b, c를 $O(n)$만에 구해본다.

이 풀이 역시 주어진 정수 배열을 정렬하였다는 가정이 있기 때문에 사용할 수 있는 방법이며, 큰 틀에서는 상술했던 풀이들과 크게 다르지 않다.

b, c를 $O(n)$만에 찾는 아이디어의 핵심은 b는 작은 수부터 골라보고, c는 큰 수부터 골라보는 것이다.

바로 예제를 통해 설명해보도록 하겠다.

아래와 같이 pa를 통해 0번째 숫자를 a로 골랐다고 가정하자.

이제, nums[pa+1:len]에서 b+c=-a인 b와 c를 찾을텐데, b는 작은 수부터 골라보고 c는 큰 수부터 골라보자.

아래 그림에서 pb는 가장 작은 수에, pc는 가장 큰 수에 위치한 것에 주목하자.

위 그림을 보면 b(=nums[pb])+c(=nums[pc])=-a(=-nums[pa])가 되는 pb, pc를 찾고자 했으나 -1(b)+3(c)>1(-a)로 -a보다 b+c가 더 커지는 상황을 만났다.

이 상황에서 우리가 할 수 있는 유일한 선택은 c를 보다 작은 수로 골라보는 것인데, 이를 이해하는 것이 조금 더 똑똑한 풀이의 핵심이다.

우리가 매 단계에서 보고 있는 b는 b로 골라볼 수 있는 후보 중 가장 작은 수이고, c는 c로 골라볼 수 있는 후보 중 가장 큰 수이다.

방금 전과 같이 가장 작은 후보(b)+가장 큰 후보(c) > 찾고자 하는 수(-a)인 상황이라면 c를 조금 더 작은 후보로 골라보는 방법 밖에는 없다.

비슷하게, 가장 작은 후보(b)+가장 큰 후보(c) < 찾고자 하는 수(-a)와 같이 반대의 대소관계였다면, b를 조금 더 큰 후보로 골라보는 방법 밖에는 없다.

이야기한 아이디어에 따라, 다음번 pb, pc의 위치는 아래의 그림과 같을 것이다.

섹션 2, 3에서의 풀이와 동일하게 pc가 중복된 숫자는 건너뛰고 있는 것에 주의하자.

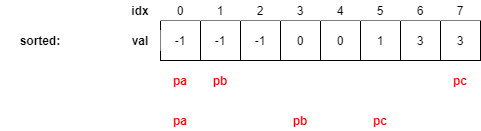
위 그림에서 볼 수 있듯이 이번에는 b(=nums[pb])+c(=nums[pc])=-a(=-nums[pa])가 되는 pb, pc를 찾았다(답에 잘 기록해주자).

이는 결국 가장 작은 후보(b)+가장 큰 후보(c) = 찾고자 하는 수(-a)인 상황을 의미하므로 다음에는 b는 보다 큰 후보로, c는 보다 작은 후보로 골라보면 된다.

따라서, pb는 5번째 숫자로(중복을 건너뛰고 있는 것에 주의하자), pc는 4번째 숫자로 아래 그림과 같이 이동하게 된다.

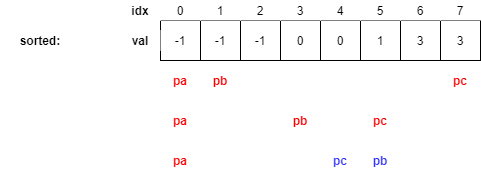
위 그림과 같이 막상 이동을 하고 보니 pb > pc인 상황이 발생하였다.

사실 너무도 자명해서 굳이 언급하지는 않았지만, 우리는 중복 없이 triplet을 출력하기 위해서 pa < pb < pc를 loop invariant로 유지해왔다.

위 그림과 같이 loop invariant가 깨질 때 b, c의 탐색을 중단해주면 된다.

충분히 감이 왔겠지만 몇 번 더해보도록 하겠다.

이제 a=-1에 대한 b, c 탐색이 끝났으므로 다음 a를 골라본다.

b는 작은 수 부터, c는 큰 수 부터 고르므로 pa, pb, pc의 위치는 아래와 같다.

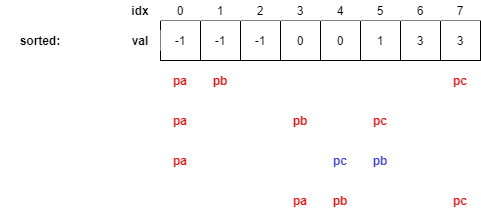
위에서 가장 작은 후보(b)+가장 큰 후보(c) > 찾고자 하는 수(-a)인 상황을 만났으므로 아래와 같이 pc를 이동시킨다.

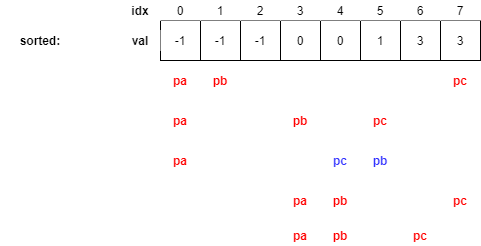
위에서 다시 한 번가장 작은 후보(b)+가장 큰 후보(c) > 찾고자 하는 수(-a)인 상황을 만났으므로 아래와 같이 또 pc를 이동시킨다.

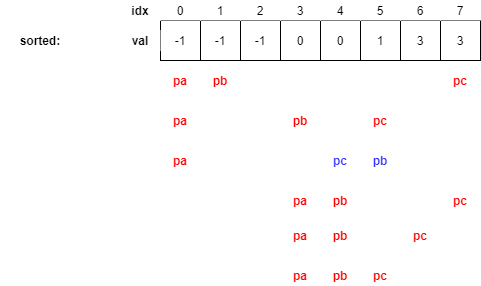
위에서 또 가장 작은 후보(b)+가장 큰 후보(c) > 찾고자 하는 수(-a)인 상황을 만났는데, 여기서는 pc가 한 번 더 이동하면 loop invariant가 깨지게되므로 a=0에 대한 b, c 탐색이 종료된다.

상술한 내용을 코드로 구현하면 아래와 같다.

vector<vector<int>> threeSum(vector<int>& nums)
{
  sort(nums.begin(), nums.end());

  vector<vector<int>> ret;

  int len = nums.size();
  int pa, pb, pc;
  int a, b, c;

  pa = 0;
  while (pa < len)
  {
    a = nums[pa];

    pb = pa + 1;
    pc = len - 1;
    while (pb < len && pb < pc)
    {
      b = nums[pb];
      c = nums[pc];
      if (b + c < -a)
      {
        // Pass the same 'b's
        while (++pb < len && nums[pb] == b)
        {
        }
      }
      else if (b + c > -a)
      {
        // Pass the same 'c's
        while (--pc >= 0 && nums[pc] == c)
        {
        }
      }
      else
      {
        ret.push_back(vector<int>{ a, b, c });
        // Pass the same 'b's
        while (++pb < len && nums[pb] == b)
        {
        }
        // Pass the same 'c's
        while (--pc >= 0 && nums[pc] == c)
        {
        }
      }
    }

    // Pass the same 'a's
    while (++pa < len && nums[pa] == a)
    {
    }
  }

  return ret;
}

알고리즘의 복잡도는 주어진 배열의 길이를 $n$이라고 할 때, 정렬에 $O(nlogn)$, a를 골라 b, c를 탐색하는데에 $O(n^2)$이므로 총 $O(n^2)$이 된다.

이렇게 풀면 91% 정도의 백분위를 받을 수 있다.