그래프 매칭

Problem link: https://www.acmicpc.net/problem/3644

일단 문제 해설에 앞서서 중요한 사실을 미리 밝히면, 이 문제의 답 범위는 64bit integer를 아득히 초과한다.

답을 계산하기 위한 BigInteger 클래스는 미리 만들어야 함에 주의하자.

아래 설명에서는 BigInteger는 이미 구현했다고 가정하고, 코어가 되는 알고리즘에 대해서만 설명한다.

문제는 DP로 접근한다.

C_(n)을 그려본 뒤에 C_(n+1)을 그려보자.

이 때, 정점 n+1에 의해서 그래프에 추가된 간선은 아래 그림의 적색과 같이 (n, n+1), (n+1, 1)이 될 것이다.

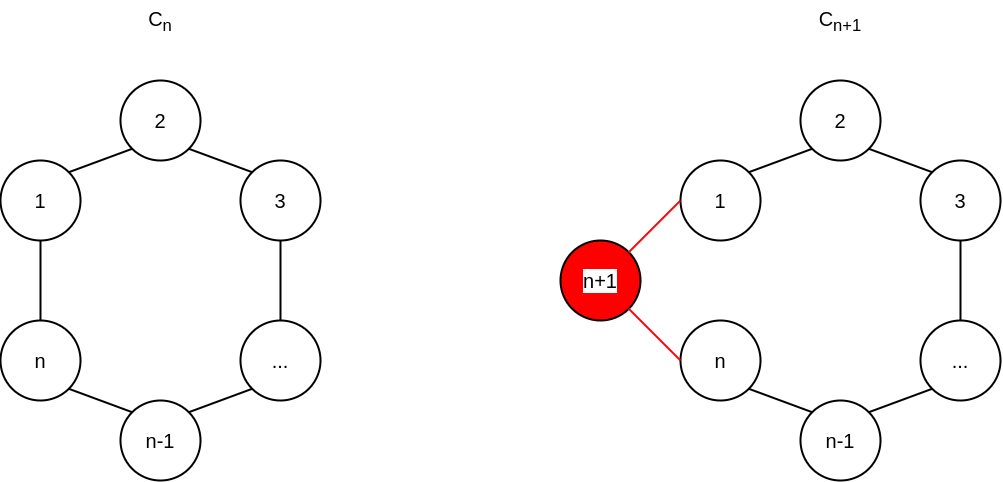
이제 C_(n+1)의 매칭 수를 헤아리는데, 아래와 같이 경우를 나누어 생각해보자.

매칭의 정의에 의해 (n, n+1), (n+1, 1)을 모두 포함할 수는 없고(n+1을 두번 포함하게 되므로), 따라서 자명하게 C_(n+1)의 매칭 수는 아래 3가지 케이스의 합이 될 것이다.

• Case1) (n, n+1), (n+1, 1) 모두를 포함하지 않는 매칭의 수
• Case2) (n, n+1)만 포함하는 매칭의 수
• Case3) (n+1, 1)만 포함하는 매칭의 수

Case 1) 의 경우에는 C_(n)에 존재하는 매칭들 중 (n, 1)을 포함하지 않는 매칭들의 수와 같음을 알 수 있다.

아래 그림이 보이듯이, (n, 1)을 포함하지 않았던 매칭들에 단순히 (n, 1)을 (n, n+1), (n+1, 1)로 바꿔치기 해놓으면 되기 때문이다.

이 때, (n, n+1), (n+1, 1) 모두 선택되지 않는 간선임에 주의하자.

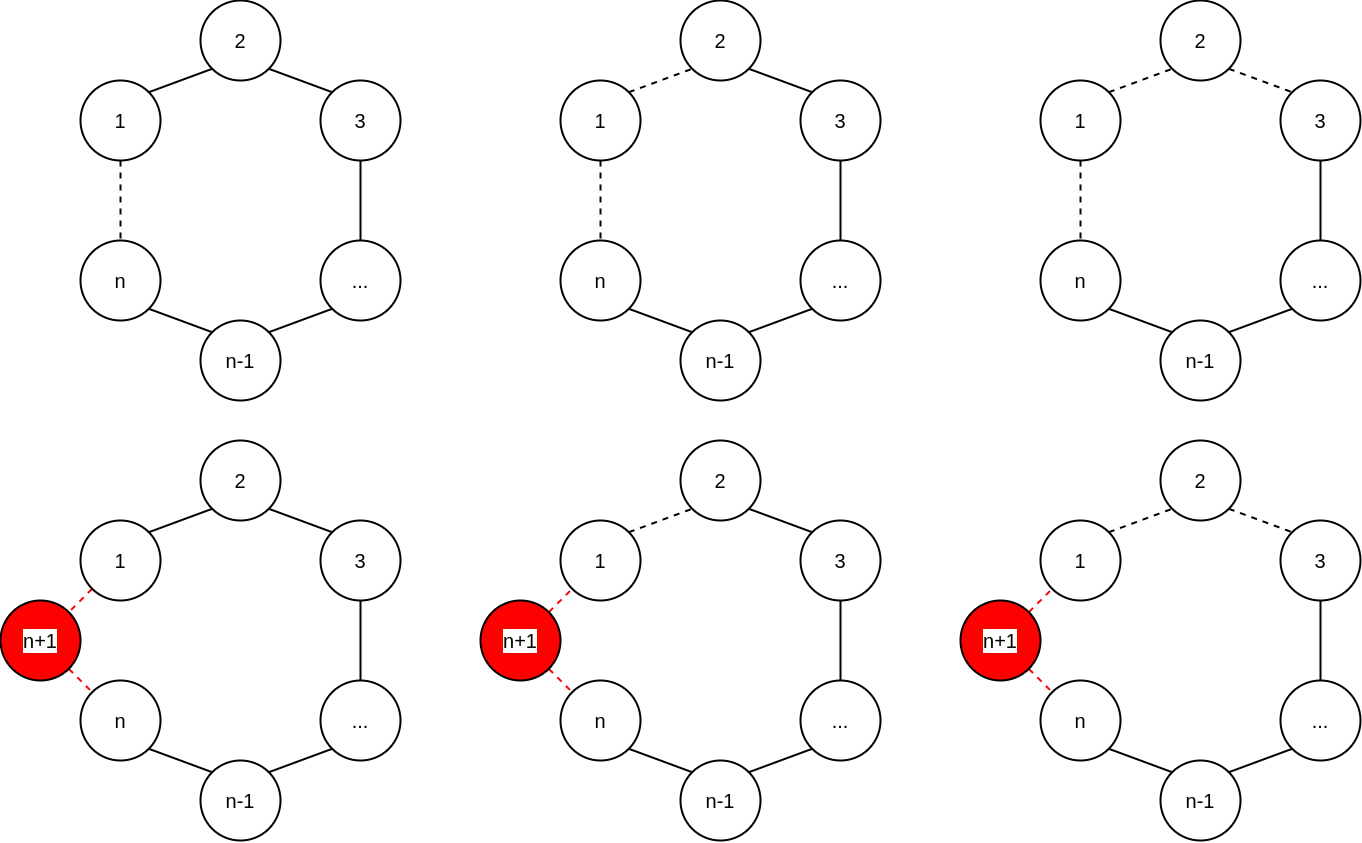
Case 2) 의 경우에는 C_(n)에 존재하는 매칭들 중 정점 n을 포함하지 않는 매칭들의 수와 같음을 알 수 있다.

그런데, 정점 C_(n)에서 정점 n을 포함하지 않는 매칭들의 수는 곧 C_(n-1)에서 (n-1, 1)을 포함하지 않는 매칭들의 수와 같다.

아래 그림이 보이듯이, (n-1, 1)을 포함하지 않았던 매칭들에 단순히 (n-1, 1)을 (n, n+1), (n+1, 1), (n-1, n)로 바꿔치기 해놓으면 되기 때문이다.

이 때, (n, n+1)은 선택된 간선, (n+1, 1), (n-1, n)은 선택되지 않는 간선임에 주의하자.

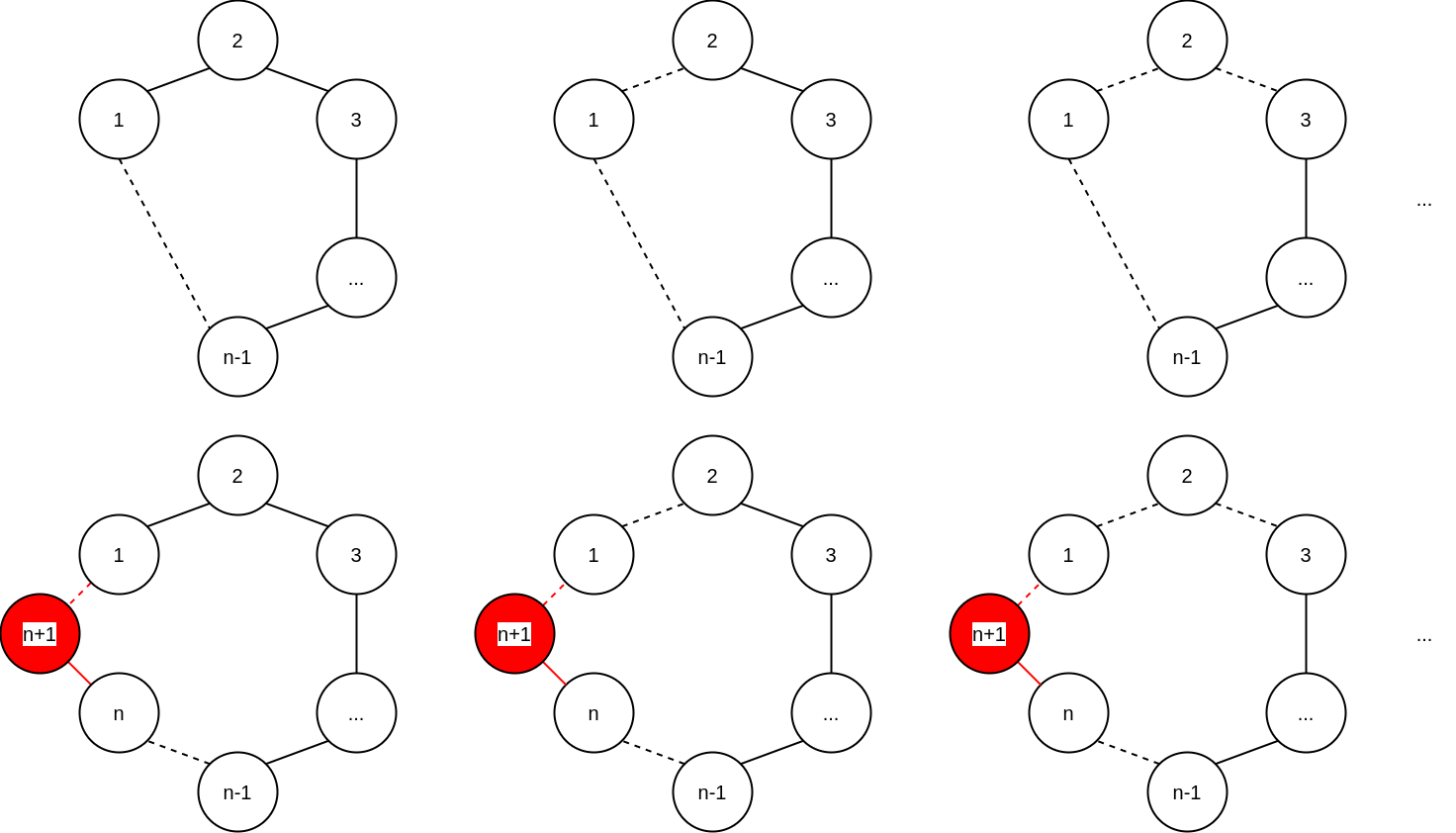
Case 3) 역시 Case 2) 와 유사하게 C_(n)의 매칭들 중 정점 1을 포함하지 않은 매칭의 수와 같음을 알 수 있다.

따라서, Case 2)와 유사한 논리의 진행이 가능한데 여기서 하나 잘 생각해볼 포인트가 있다.

주어지는 그래프는 굉장히 특이한 환형의 그래프이므로 정점 1을 포함하지 않는 경우의 수나, 정점 2를 포함하지 않는 경우의 수나..., 특정한 하나의 정점을 포함하지 않는 경우의 수는 모두 같을 수 밖에 없다.

따라서, Case 3)의 매칭 수는 Case 2)의 매칭 수와 같다.

아이디어를 DP로 옮기기 위한 CACHE의 정의는 아래와 같다.

• CACHE[n][0]: C_(n)에서 간선 (n, 1)을 포함하지 않는 매칭의 수
• CACHE[n][1]: C_(n)에 존재하는 매칭의 수

점화식을 세우면 아래와 같다.

• CACHE[n+1][0] = CACHE[n][0] + CACHE[n-1][1] // Case 1) + Case 3)
• CACHE[n+1][1] = CACHE[n][0] + 2 * CACHE[n-1][0] // Case 1) + Case 2) + Case 3)

#include <iostream>
#include <string>
#include <algorithm>

using namespace std;

class Number
{
private:
  string number_;

public:
  Number(void) = default;
  Number& operator=(const Number& rhs) = default;

  explicit Number(const string& number) : number_(number)
  {
  }

  const std::string& number(void) const
  {
    return number_;
  }

  Number operator+(const Number& rhs) const
  {
    string result;

    size_t length = max(number().size(), rhs.number().size());

    size_t sum;
    size_t carry = 0;
    for (size_t digit = 0; digit < length; ++digit)
    {
      char digit_a = (number().size() >= digit + 1) ? number()[number().size() - digit - 1] : '0';
      char digit_b = (rhs.number().size() >= digit + 1) ? rhs.number()[rhs.number().size() - digit - 1] : '0';

      sum = ((digit_a - '0') + (digit_b - '0') + carry) % 10;
      carry = ((digit_a - '0') + (digit_b - '0') + carry) / 10;

      result += string(1, static_cast<char>(sum + '0'));
    }

    if (carry)
    {
      result += string(1, static_cast<char>(carry + '0'));
    }

    reverse(result.begin(), result.end());
    return Number(result);
  }
};

const int kMaxN = 10000;
Number CACHE[kMaxN + 1][2];

int main(void)
{
  // For Faster IO
  ios_base::sync_with_stdio(false);
  cout.tie(nullptr);
  cin.tie(nullptr);

  // Preprocessing
  CACHE[3][0] = Number("3");
  CACHE[3][1] = Number("4");
  CACHE[4][0] = Number("5");
  CACHE[4][1] = Number("7");

  for (int n = 5; n <= kMaxN; ++n)
  {
    CACHE[n][0] = CACHE[n - 1][0] + CACHE[n - 2][0];
    CACHE[n][1] = CACHE[n - 1][0] + CACHE[n - 2][0] + CACHE[n - 2][0];
  }

  // Solve
  int N;
  while (cin >> N)
  {
    cout << CACHE[N][1].number() << '\n';
  }

  return 0;
}