[코딩테스트] 하노이 탑 - 재귀

바킹독의 실전 알고리즘 강의를 참고하여 공부한 내용입니다.

참고 자료

바킹독의 실전 알고리즘 - 재귀

https://youtu.be/8vDDJm5EewM?si=SUESkBHrCnthuNwM

백준 11729번 : 하노이 탑 이동 순서

https://www.acmicpc.net/problem/16947

---

하노이 탑이란?

아래의 조건을 지키며 n개의 원판을 기둥1에서 기둥3으로 옮기는 것을 의미한다.

조건

• 한번에 하나의 원판만 이동할 수 있다.
• 작은 원판 위에 큰 원판을 둘 수 없다.
• 가장 상단에 있는 원판만 이동할 수 있다.

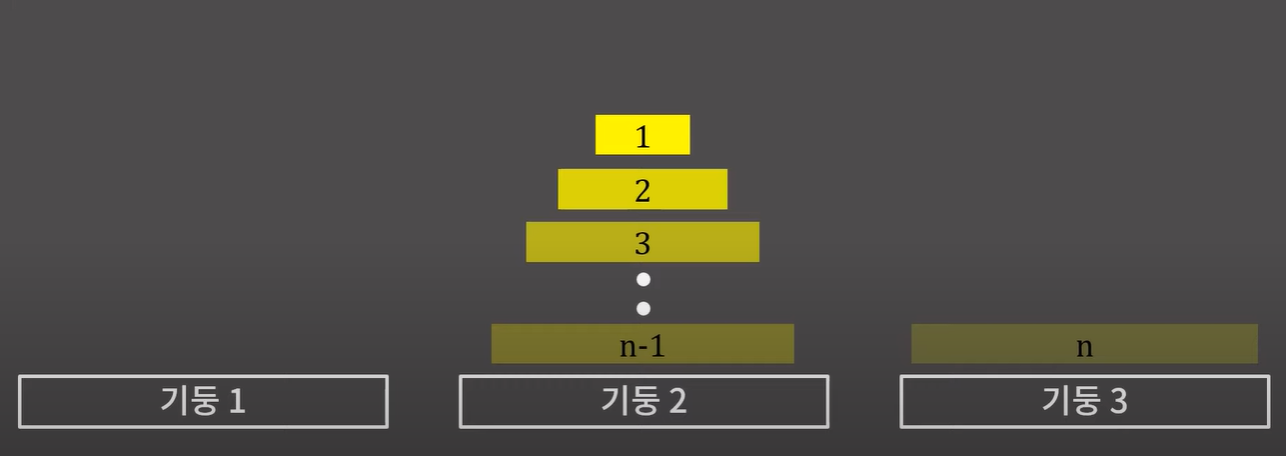
n개의 원판을 옮기기 위해서는, 결국 n번 원판을 기둥1에서 기둥3으로 옮겨야 한다.
이를 위해서는 n-1번까지의 원판들이 모두 기둥2로 옮겨져 있어야 한다.
=> 즉, n-1개의 원판을 이동할 수 있으면 n개의 원판도 이동할 수 있다.

원판 n개를 a번 기둥에서 b번 기둥으로 옮기는 방법을 출력하는 함수를 짜면 해당 문제를 해결할 수 있다.

base condition

• 가장 상단의 원판만 이동할 수 있으므로 base condition(재귀 함수의 종료 조건)을 n이 1일때로 설정하고, a번 기둥에서 b번 기둥으로 옮긴다.

if (n == 1)
    {
        cout << a << ' ' << b << '\n';
        return;
    }

재귀 식

• n-1개의 원판을 경유지 기둥으로 옮긴다. 기둥 번호의 합(1, 2, 3)이 6이므로 6-a-b번 기둥이 경유지 기둥이다.

func(a, 6 - a - b, n - 1);

• n번 원판을 목적지 기둥으로 옮긴다.

cout << a << ' ' << b << '\n';

• n-1개의 원판을 경유지 기둥에서 목적지 기둥으로 옮긴다.

func(6 - a - b, b, n - 1);

• 정답 코드

#include <iostream>
#include <cmath>
using namespace std;

// 원판 n개를 a번 기둥에서 b번 기둥으로 옮기는 방법을 출력하는 함수
void func(int a, int b, int n)
{
    if (n == 1)
    {
        cout << a << ' ' << b << '\n';
        return;
    }

    func(a, 6 - a - b, n - 1);
    cout << a << ' ' << b << '\n';
    func(6 - a - b, b, n - 1);
}

int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);

    int num = 0;
    cin >> num;

    cout << (int)(pow(2, num) - 1) << '\n';
    func(1, 3, num);

    return 0;
}

귀납적으로 사고해야 하지만 나는 절차지향적 인간이기 때문에.. 원판이 3개라고 가정하고 코드 흐름을 적어보았다.

원판 이동 횟수

T(n) = 2 * T(n-1) + 1

한 기둥에 차례로 꽂혀있는 n개의 원판을 특정 기둥으로 옮기는 횟수가 T(n)이라고 가정하면, n-1개의 원판을 옮기는 횟수는 T(n-1)이다. 해당 코드에서 n-1개의 원판을 경유지 기둥으로 이동하고, 가장 큰 원판을 목적지 기둥으로 이동하고, 경유지 기둥의 n-1개의 원판을 다시 목적지 기둥으로 이동한다. 따라서 T(n) = 2 * T(n-1) + 1 가 성립한다.

=> T(n)에 차례로 대입하며 풀어보면, 2^n -1 이라는 규칙을 발견할 수 있다.