인덱스로서의 트리는 높이가 중요하다! 검색 속도와 연관된다.

BST : Binary Search Tree(이진 탐색 트리)

특정 데이터 검색, 노드 삽입/삭제가 자주 발생하는 문제에 가장 효과적인 이진트리
왼쪽/오른쪽이라는 방향성을 가지며 다루기 편리
부모 노드를 중심으로 왼쪽은 부모 노드보다 작은 데이터, 오른쪽은 부모보다 큰 데이터 위치
일반적으로 노드 수가 많아지면 트리 높이가 커진다.

MST : m-way Search Tree(m원 탐색 트리)

m개의 서브 트리를 가질 수 있는 트리
(같은 수의 노드를 가질때 BST보다 높이가 낮다.)
이진 탐색 트리의 확장된 형태
탐색 트리의 제한을 따르되 2개 이상 m개 이하의 자식을 가질 수 있다.

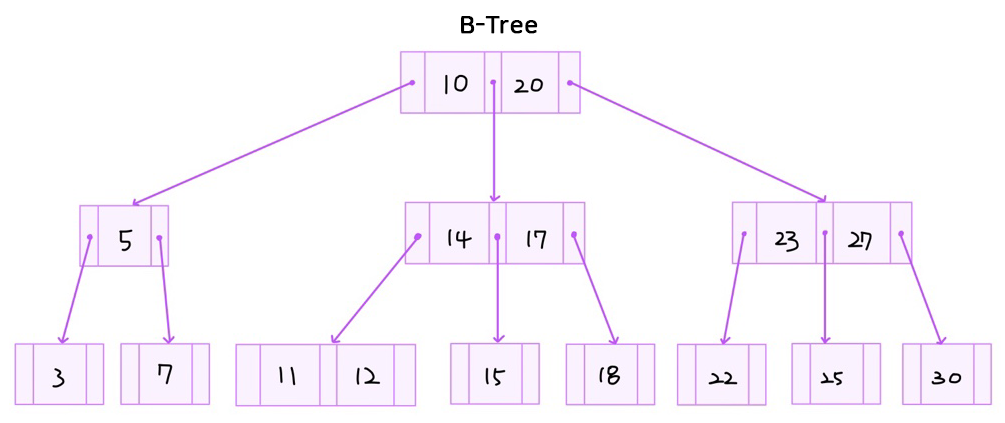
B-Tree

기본 MST이고 균형 트리(Balanced MST)
→ 한쪽으로 쏠리는 트리가 나오는 것 방지
(균형 트리? 루트로부터 리프까지의 거리가 일정한 트리)
노드의 데이터 수가 n개라면 자식의 수는 n+1개
루트와 리프를 노드를 제외한 노드들은 최소 [m/2]개의 서브트리를 갖는다.
노드의 데이터는 반드시 정렬된 상태여야한다.
자식 노드의 데이터들은 노드를 기준으로 데이터보다 작은 값은 왼쪽 서브트리에 큰 값은 오른쪽 서트리에 위치
리프 노드로 가는 경로의 길이는 모두 같아야한다. (리프 노드는 모두 같은 레벨에 존재해야함)

B+Tree

B-Tree와 유사하지만 리프노드는 연결리스트의 형태를 띄어 선형검색이 가능하다.(순차 탐색에 유리)
무조건 리프노드까지 가야만 찾을 수 있다.
작은 시간복잡도에 검색을 수행할 수 있음
실제 DB 인덱싱은 B+ Tree로 이루어져있다.
(인덱싱 - 어떤 자료를 찾는데 key값을 이용해 효과적으로 찾을 수 있는 기능)
리프가 아닌 노드로 된 인덱스 세트와 리프 노드로 구성된 순차 세트로 구성

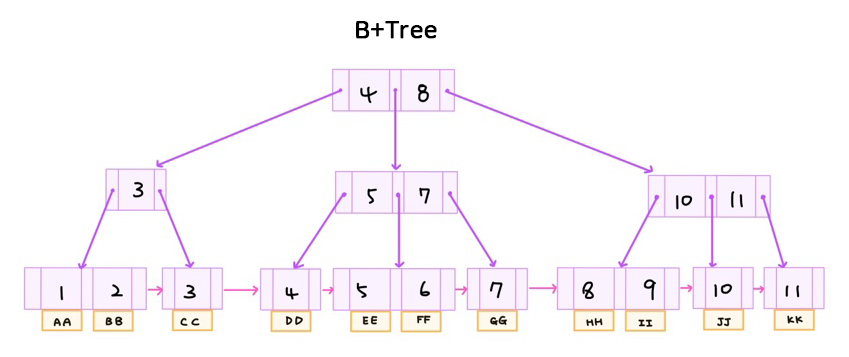
• 모든 key, data가 리프노드에 모여있다.
• 모든 리프는 같은 레벨이 있다.
• 루트는 0/2 또는 [m/2]에서 m개 사이의 서브 트리를 갖는다.
• 루프/리프를 제외한 모든 노드는 최소 [m/2]개, 최대 m개의 서브 트리를 갖는다.
• 리프는 데이터 파일의 순차 세트를 나타내며 연결리스트의 형태이다.
• 리프가 아닌 노드에 있는 키값의 수는 그 노드의 서브 트리 수보다 하나 적다.

<삽입 / 삭제 추가 정리 이해 필요>

삽입

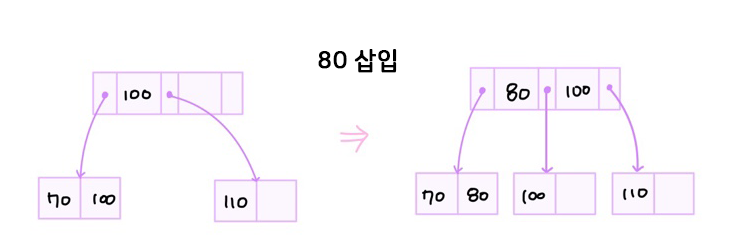
70과 100의 중간 값인 80을 위로 올리고 노드 70, 100은 분열
새로운 데이터는 리프노드에 삽입

• 노드의 분열이 일어나면 중간 key값이 부모 노드로 올라가고 새로 분열된 노드에도 포함되어야한다.
• 새 노드는 리프노드끼리의 연결리스트에도 삽입되어야한다.

삭제

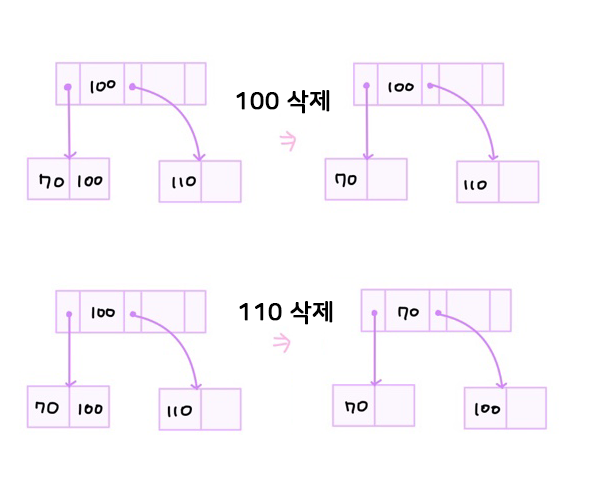
1. 리프노드에 있는 100 삭제
(인덱스 셋에 있는 100은 삭제 하지 않는다 - 노드의 키값 탐색에 필요한 분기 값으로 사용될 수 있음)
2. 리프노드에 있는 110삭제

• 인덱스 셋 부분은 다른 key값을 찾는데 사용될 수 있으므로 리프노드의 값이 삭제되어도 삭제하지 않는다.
• 재배치할 경우 인덱스 셋 부분의 노드의 key값은 변하지만 트리 구조는 변하지 않는다.
• 합병을 할 경우 인덱스 셋 부분에서도 key값을 삭제한다.
• 재배치와 합병이 필요하지 않을때는 리프노드에서만 삭제