Binary Heap

우선순위 큐(Priority Queue)를 구현하기 가장 좋은 구조

Binary Heap이 되기 위한 2가지 속성

• Share Property
  완전 이진 트리의 구조를 유지해야 함
• Heap Property
  부모의 우선순위가 자식의 우선순위보다 높아야함
  부모의 값이 자식값보다 항상 크다/작다
  → 부모 자식 요소의 관계만 일정하면 된다!

Binary Heap 분류

우선순위에 따라 2가지로 분류

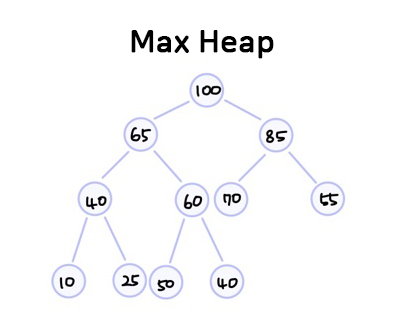
• 최대 힙(Max Heap)
  key(parent) ≥ key(child)
  부모 노드의 키 값이 자식 노드의 키 값보다 크거나 같은 완전 이진 트리
  가장 큰 값이 루트노드에 있다.
  
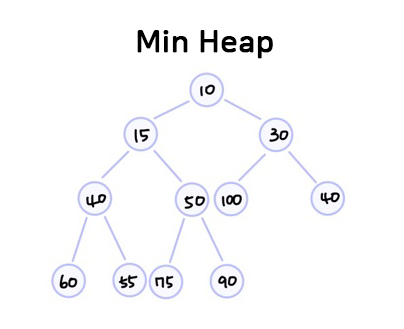
• 최소 힙(Min Heap)
  key(parent) ≤ key(child)
  부모 노드의 키 값이 자식 노드의 키 값보다 작거나 같은 완전 이진 트리
  가장 작은 값이 루트노드에 있다.
  
  

Binary Heap 연산

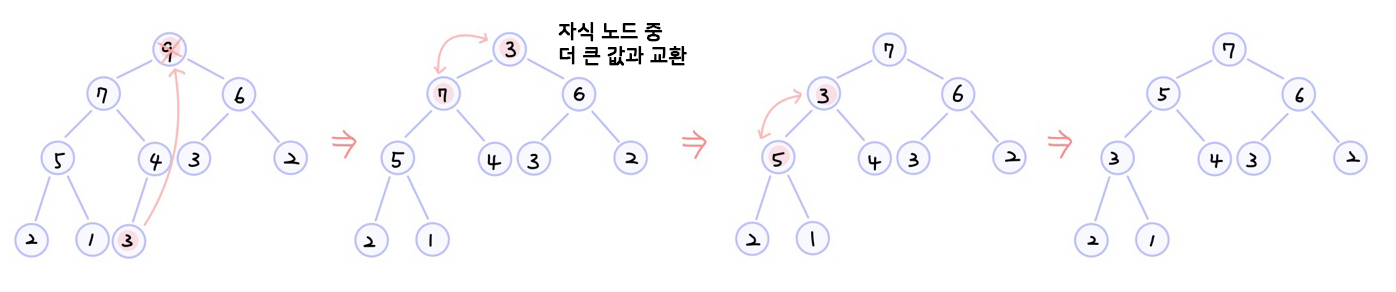
• 삽입 연산
  1. 완전 이진 트리의 조건이 만족하도록 노드를 추가
  2. 부모 노드와 크기 조건이 만족하도록 삽입 원소 위치를 찾는다
     (최대힙)현재 부모 노드 키값 > 삽입 원소 키값
     (최소힙)현재 부모 노드 키값 < 삽입 원소 키값
     관계가 성립하지 않으면 서로 자리를 바꾼다.
     
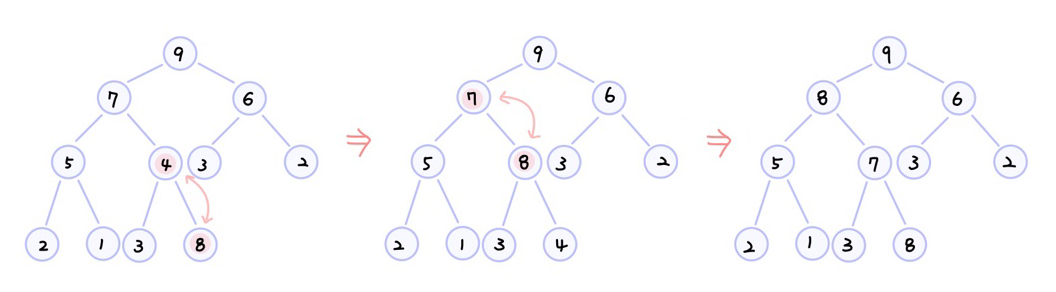
• 삭제 연산
  1. 루트 노드의 원소를 삭제하여 반환
  2. 노드 개수가 n-1개인 이진트리로 조정한다
     → n번째 노드의 원소는 루트노드에 임시저장
  3. 완전 이진 트리 내에서 루트에 임시 저장된 원소의 제자리를 찾는다.
     (최대힙)임시 저장 원소의 키값 > 현재 자식 노드 키값
     (최소힙)임시 저장 원소의 키값 < 현재 자식 노드 키값
     관계가 성립하지 않으면 서로 자리를 바꾼다.