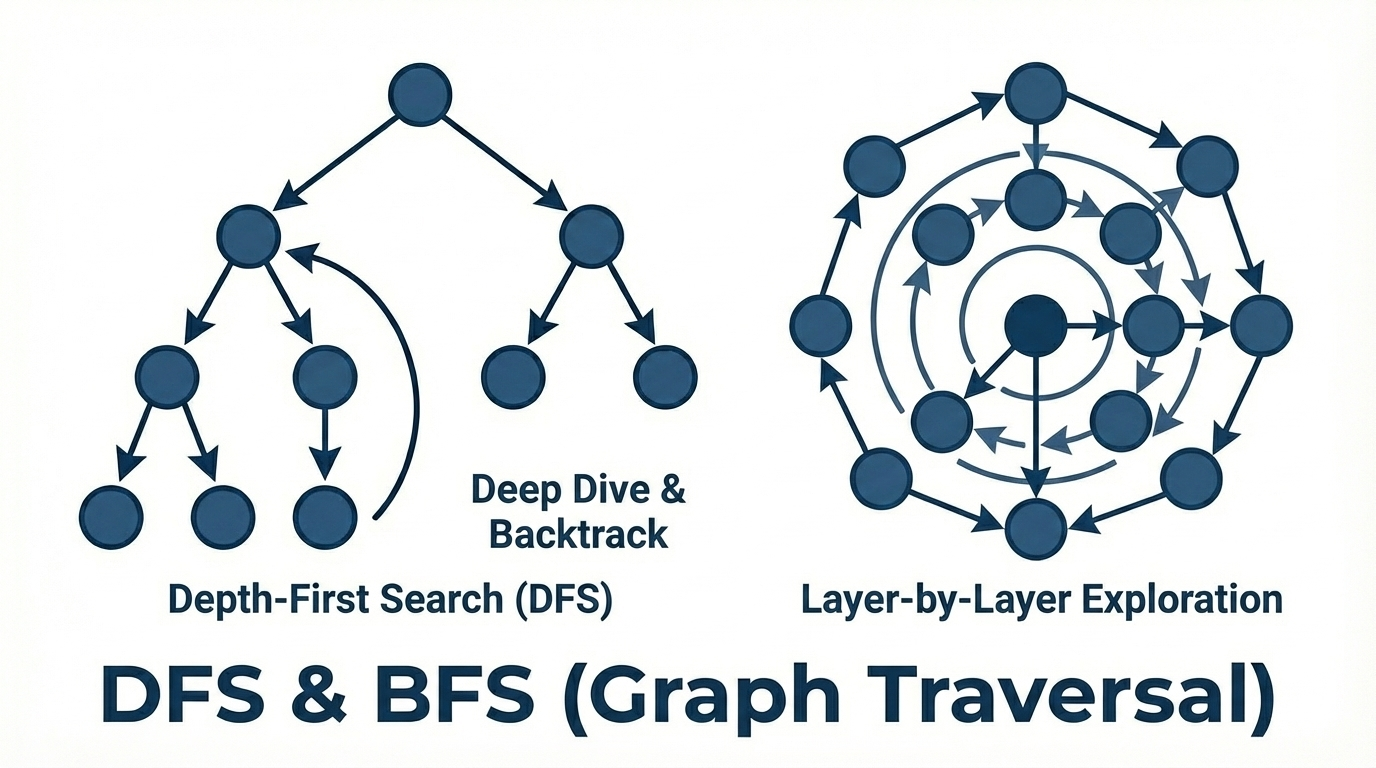
그래프 구조: 정점(Node)과 간선(Edge)
그래프 탐색의 두 가지 전략
- 깊이 우선 탐색(DFS, Depth-First Search)
- 너비 우선 탐색(BFS, Breadth-First Search)
-> 두 전략 모두 방문한 노드를 기록하는 것이 중요!
DFS
- 동작 방식
- 현재 노드에서 아직 방문하지 않은 이웃 노드를 하나 선택하여 깊이 들어간다.
- 더 이상 갈 곳이 없으면 이전 노드로 돌아온다.(백트래킹)
- 이웃 노드가 존재할 때까지 이전 노드로 돌아간다.
- 이웃 노드가 존재하면 모든 노드를 반복할 때까지 1~3번 과정을 반복한다.
- 핵심 도구
- 스택(방금 방문한 노드에서 깊게 들어가야 하기 때문에 최근에 추가된 이웃들 먼저 탐색)
- 재귀함수
1) 리스트를 활용한 DFS
graph = {} # 딕셔너리
graph['A'] = ['B', 'C'] # {'A': ['B', 'C']}
graph['B'] = ['A', 'D']
graph['C'] = ['A', 'G', 'H', 'I']
graph['D'] = ['B', 'E', 'F']
graph['E'] = ['D']
graph['F'] = ['D']
graph['G'] = ['C']
graph['H'] = ['C']
graph['I'] = ['C', 'J']
graph['J'] = ['I']
# need_visited방문(pop) ---(방문하지 않은 노드면)---> visited에 노드 추가 -> 해당 노드의 이웃 노드를 need_visited에 추가 ---(need_visited가 비어있으면)---> visited 반환
# ---(비어있지 않으면) ------------> 처음으로
# ----(방문한 노드면) -> 처음으로
def dfs(graph, start_node):
need_visited, visited = [], [] # 방문할 노드, 방문한 노드
need_visited.append(start_node) # 시작 노드
# 방문할 노드가 남아있을 때까지
while need_visited:
node = need_visited.pop() # 가장 마지막 데이터 꺼내기(가장 최근에 들어간 데이터)
# 그 노드가 방문한 리스트에 없으면
if node not in visited:
visited.append(node) # 방문한 리스트에 추가하기
need_visited.extend(graph[node]) # 방문한 노드와 인접한 노드들을 방문할 리스트에 추가
# append()는 리스트를 통째로 추가하는 반면에, extend()는 리스트 껍질을 벗겨서 요소를 추가
return visited
print(dfs(graph, 'A')) # ['A', 'C', 'I', 'J', 'H', 'G', 'B', 'D', 'F', 'E']⬇️아래는 시간 복잡도를 줄이기 위해 list 대신 deque(덱)를 사용하여 구현한 예제이다.⬇️
2) deque를 활용한 DFS
from collections import deque
def dfs2(graph, start_node):
visited = []
need_visited = deque() # 스택을 덱(deque)로 구현
need_visited.append(start_node) # 시작 노드 추가
# 방문할 노드가 남아있으면
while need_visited:
node = need_visited.pop() # 오른쪽 끝 노드 제거(가장 최근에 추가된 노드)
# 방문한 이력이 없는 노드이면
if node not in visited:
visited.append(node) # 방문 리스트에 추가
need_visited.extend(graph[node]) # 인접 노드들을 방문할 스택에 추가
return visited
print(dfs2(graph, 'A')) 🙂재귀를 이용해 dfs를 구현하는 방식도 있는데, 그건 추후에 추가하도록 하겠다.
BFS
- 동작 방식
- 시작 노드를 방문하고, 이 노드의 모든 이웃을 큐에 넣는다.
- 큐에서 원소 하나를 꺼내서 방문하고, 방문한 노드의 이웃들을 큐에 넣는다.
- 큐가 빌 때까지 2번 과정을 반복한다.
- 핵심 도구
- 큐(이웃들을 연속해서 방문해야하기 때문)
deque를 활용한 BFS
from collections import deque
def bfs(graph, start_node):
visited = []
need_visited = deque() # 큐를 덱(deque)으로 구현
need_visited.append(start_node) # 시작 노드를 방문할 큐에 추가
# 방문할 노드가 남아있으면
while need_visited:
node = need_visited.popleft() # 왼쪽 끝 노드 제거(가장 예전에 추가된 노드)
# 제거된 노드에 방문한 이력이 없으면
if node not in visited:
visited.append(node) # 방문 리스트에 추가
need_visited.extend(graph[node]) # 인접 노드들을 방문할 큐에 추가
return visited
print(bfs(graph, 'A')) # ['A', 'B', 'C', 'D', 'G', 'H', 'I', 'E', 'F', 'J']
📋관련 문제
https://www.acmicpc.net/problem/2606