시간복잡도

시간복잡도 (Time Complexity)

알고리즘의 시간복잡도란 함수가 입력된 값을 처리하는데 걸리는 시간을 측정한 값!
일반적으로 Big O 기호를 사용해서 표현.

시간 복잡도의 입력값 크기는 점근적(asymptotically)으로 증가해서 결국 무한대까지 갈 수 있음.
시간 복잡도의 측정 방법은 알고리즘이 수행하는 기본적인 연산이 몇개인지를 세어서 확인함.

시간복잡도는 굉장히 다양한 방식으로 가능하지만, 일단 HA시간에 다룬 메인 개념 위주로 정리

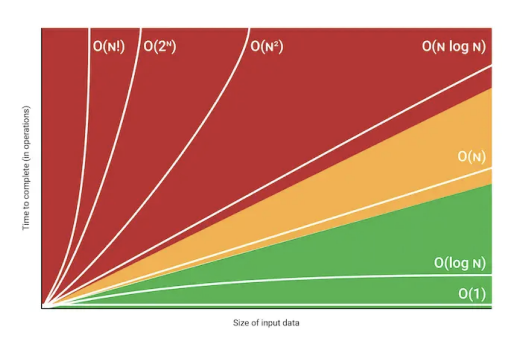
constant - O(1)

• 입력 데이터의 크기에 상관없이 언제나 일정한 시간이 걸리는 알고리즘. 데이터가 얼마나 증가하든 성능에 영향을 미치지 않는다.
• 예) 정수가 홀수인지 짝수인지 결정하기

logarithmic - O(log n)

• 입력데이터의 크기가 커질수록 처리 시간이 로그만큼 짧아지는 알고리즘. 예를들어 데이터가 10배가 되면 처리 시간은 2배가 된다. 이진 탐색이 대표적이며, 재귀가 순기능으로 이루어지는 경우도 이에 해당한다.
• 예) 이진 검색 (Binary search)

linear time - O(n)

• 입력 데이터의 크기에 비례해 처리 시간이 증가하는 알고리즘. 예를들어 데이터가 10배가 되면, 처리 시간도 10배가 된다. 선형 탐색 알고리즘이 대표적인 케이스.
• 예) 정렬되지 않는 배열에서 가장 작은 항목을 찾기

quadratic - O(n²)

• 데이터가 많아질수록 처리시간이 급수적으로 늘어나는 알고리즘. 예를들어 데이터가 10배가 되면 처리 시간은 최대 100배가 된다.
• 예) 이중 루프(n² matrix)

exponential - O(2ⁿ)

• 데이터량이 많아질수록 처리시간이 기하급수적으로 늘어나는 알고리즘.
• 예) 피보나치, 재귀가 역기능하는 경우