[BOJ 14565] 역원(Inverse) 구하기

문제

BOJ 14565 역원구하기

유형

• 수학
• 확장 유클리드 호제법

풀이

확장 유클리드 호제법이라는 알고리즘을 써서 푸는 문제였다.

확장 유클리드 호제법은 at + bs = gcd(a,b)라는 식에서 t,s값을 구하는 방법으로 여기를 참조하였다.

핵심은

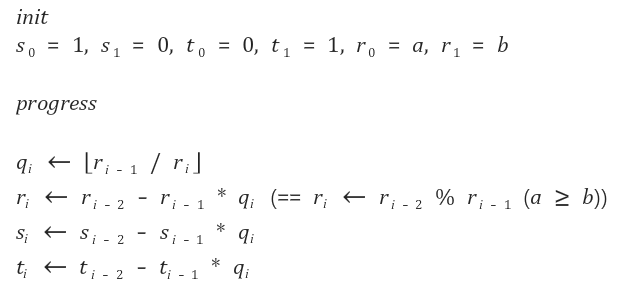
위 과정을 따라서 ri가 0이 될때까지 반복하면 된다.

식에서 a,b 문제에서는 a,n이 서로 서로소일 때 곱셈의 역원을 구할 수 있다고 설명되어있다. 그래서 a와 n이 서로소가 아니면 -1을 출력하고 서로소이면 위 알고리즘을 따라서 풀면 풀리는 문제였다. 솔직히 알고리즘 자체를 이해하지는 못하겠다.

덧셈의 역원은 그냥 n - a로 구할 수 있다.

코드

#include <bits/stdc++.h>

const int dx[4] = { 1,0,-1,0 };
const int dy[4] = { 0,-1,0,1 };

using namespace std;
long long n, a;

long long gcd(long long  x, long long y) {
	if (y == 0) return x;
	else return gcd(y, x % y);
}

int main() {
	cin.tie(0); cout.tie(0); ios_base::sync_with_stdio(false);
	cin >> n >> a;

	cout << n - a << ' ';

	if (gcd(n, a) != 1) cout << -1;
	else {
		vector<long long> s, t, r, q;
		s = { 1, 0 };
		t = { 0, 1 };
		r = { a, n };

		while (true) {
			long long r2 = r[r.size() - 2];
			long long r1 = r[r.size() - 1];
			q.push_back(r2 / r1);
			r.push_back(r2 % r1);

			if (r[r.size() - 1] == 0) break;

			long long s2 = s[s.size() - 2];
			long long s1 = s[s.size() - 1];

			long long t2 = t[t.size() - 2];
			long long t1 = t[t.size() - 1];

			long long q1 = q[q.size() - 1];
			s.push_back(s2 - s1 * q1);
			t.push_back(t2 - t1 * q1);
		}

		cout << (s[s.size() - 1] + n) % n;
	}


	return 0;
}