활성화 함수의 정의, 종류 및 파이썬으로 각 함수의 plot을 그리는 방법에 대해 알아보겠습니다.
활성화 함수란 뉴런끼리의 화학 신호가 전달 될 때 이용되는 활성화 함수에서 착안해 신경망 학습에서 입력받은 신호를 학습에 이용될 수 있게 출력 신호로 처리하는 함수를 뜻합니다.
딥러닝의 핵심은 입력 데이터를 기반으로 expectation(기댓값) 에 가깝게 만드는 유용한 표현(representation)을 학습(learning)하는 것입니다.
실제 데이터셋들은 linearity가 성립되는 경우가 아주 적기 때문에 Linear model 만으로 신경망을 구축하는 것은 성능이 좋지 않을 수 밖에 없습니다.
아무리 층을 세분화해서 선형결합을 여러번 하더라도 계속 선형모델이기 때문에 실제 알고리즘과는 동떨어진 모델이 나올 수 밖에 없습니다.
따라서 비선형성을 추가해주기 위해 활성화 함수를 거치는 작업을 진행해줍니다.
1) Sigmoid Function
모든 실수 값을 구간 (0,1) 에 있는 미분 가능한 수로 변환하는 특징을 갖기 때문에, Logistic Classification과 같은 분류 문제에 많이 사용됩니다.
시그모이드 함수를 미분하면 최대치가 0.25 로, 1보다 작기 때문에 계속 곱하면 0에 수렴하게 됩니다.
따라서 역전파 알고리즘에서 여러 층을 거칠수록 기울기가 작아져 처음 층까지 전달되지 않는 기울기 소실(vanishing gradient) 문제가 발생해 가중치를 수정하기 어렵다는 단점이 있습니다.
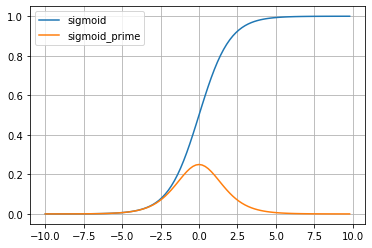
import numpy as np
import matplotlib.pyplot as plt
# 시그모이드 함수
def sigmoid(x):
return 1 / (1+np.exp(-x))
# 시그모이드 함수의 도함수
def sigmoid_prime(x):
sig = sigmoid(x)
return sig * (1 - sig)
# 시그모이드 함수, 도함수 그래프 그리기
x_range = np.arange(-10, 10, 0.2)
y_range = np.array([sigmoid(x) for x in x_range])
y_prime = np.array([sigmoid_prime(x) for x in x_range])
plt.plot(x_range, y_range, label = 'sigmoid')
plt.plot(x_range, y_prime, label = 'sigmoid_prime')
plt.grid(which = 'major') # 그리드 표현
plt.legend() # 레전드(범례) 표현
plt.show()2) Tanh Function (Hyperbolic Tangent)
sigmoid 함수의 단점을 보완하기 위해 나온 함수로 성능이 더 좋습니다.
하이퍼볼릭탄젠트 함수는 sigmoid 함수를 다음과 같이 transformation해서 얻을 수 있습니다.
-1 vertical shift & 1/2 horizontal squeeze & 2 vertical stretch
입력신호를 -1과 1 사이 값으로 정규화해줍니다.
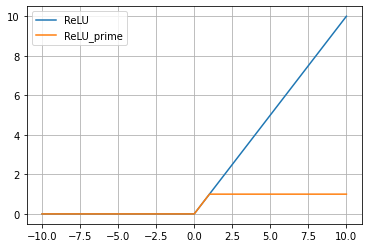
# 하이퍼볼릭탄젠트 함수
def tanh(x):
return (np.exp(x) - np.exp(-x))/(np.exp(x) + np.exp(-x))
# 하이퍼볼릭탄젠트 함수의 도함수
def tanh_prime(x):
tan = tanh(x)
return 1 - tan**2
# ReLU 함수와 도함수 그래프
x_range = np.arange(-10, 10, 0.2)
y_range = np.array([tanh(x) for x in x_range])
y_prime = np.array([tanh_prime(x) for x in x_range])
plt.plot(x_range, y_range, label = 'tanh')
plt.plot(x_range, y_prime, label = 'tanh_prime')
plt.grid(which = 'major') # 그리드 표현
plt.legend() # 레전드(범례) 표현
plt.show()3) ReLU Function (Rectified Linear Unit)
ReLU 함수는 최근 가장 보편적으로 쓰이는 활성화 함수입니다.
입력값이 0보다 작을 때는 모든 값을 0으로 처리하고, 0보다 큰 값은 입력값 그대로를 사용합니다.
exp() 함수를 사용하지 않아 sigmoid나 tanh보다 각각 1.5배, 2배 빠르게 학습된다고 합니다.
출력값으로 0이 많아 계산하는 시간과 메모리가 적다는 장점이 있고 잠재적으로 오버피팅을 막아줍니다.
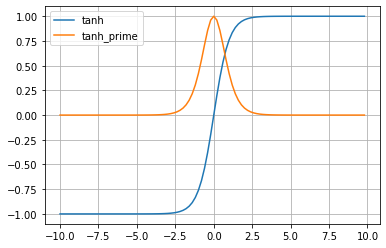
# ReLU 함수
def relu(x):
return max(0.0, x)
# ReLU 함수의 도함수
def relu_prime(x):
if x > 0:
return 1
else:
return 0
# ReLU 함수와 도함수 그래프
x_range = np.arange(-10, 11)
y_range = np.array([relu(x) for x in x_range])
y_prime = np.array([relu_prime(x) for x in x_range])
plt.plot(x_range, y_range, label = 'ReLU')
plt.plot(x_range, y_prime, label = 'ReLU_prime')
plt.grid(which = 'major') # 그리드 표현
plt.legend() # 레전드(범례) 표현
plt.show()