BFS(너비 우선 탐색) 그리고 DFS(깊이 우선 탐색)

JJAE WON·2022년 9월 28일

BFS란?

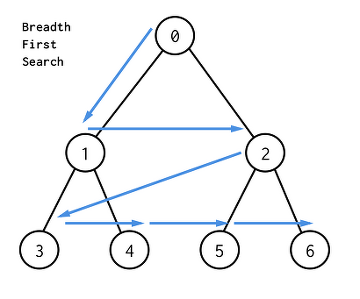
루트 노드(혹은 다른 임의의 노드)에서 인접한 노드를 먼저 탐색 하는 것

시작 정점으로 부터 가까운 정점을 먼저 방문 하는 방법
넓게 탐색하는 것
사용하는 경우 - 두 노드 사이의 최단 경로 , 임의의 경로를 찾고 싶을 때
DFS에 비해 조금 복잡하지만 속도는 빠르다.
Queue를 사용한다.(FIFO)

방법

시작 노드를 큐에 넣는다.
큐에서 꺼내면서 인접한 노드를 전부 넣는다.
앞에서 부터 꺼내면서 인접한 노드들을 방문했는지 확인한다.

3-1. 모두 방문했다면 다음 노드를 꺼낸다.

3-2. 모두 방문하지 않았다면 방문안한 노드를 현재 큐 맨 뒤에 넣어준다.
큐가 빌때까지 2~3번을 반복한다.

/** graph의 형태 
[[], [1번과 인접한 정점], [2번과 인접한 정점..], .... ]
**/

fun bfs(graph : Array<MutableList<Int>>,size : Int,start : Int){
    graph.forEach { it.sort() }
    val visited = Array(size+1){false}
    val queue = mutableListOf<Int>()

    queue.add(start) // 초기 정점 큐에 추가
    visited[start] = true // 초기 정점 자동 방문
    print("$start ")

    while (queue.isNotEmpty()){ //큐가 완전히 빌 때까지 반복
        val front = queue.removeFirst() // 맨앞 가져오기
        graph[front].forEach { // 맨앞에 있는 값과 인접한 얘들 전부 queue에 넣기
            if (!visited[it]){
                queue.add(it)
                visited[it] = true
                print("$it ")
            }
        }
    }
}

DFS란?

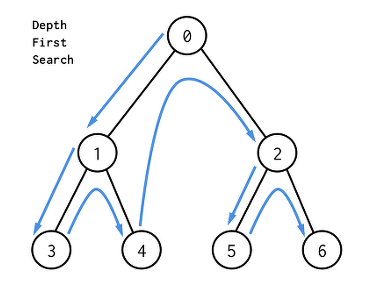
루트(혹은 다른 임의의 노드)에서 시작해서 다음분기로 넘어가기 전에 해당 분기를 완벽하게 탐색 하는 법

미로를 탐색하는 것과 유사
사용하는 경우 - 모든 노드를 방문하고자 할 때
BFS에 비해 단순하지만 조금 느리다.
순환 알고리즘의 형태
재귀또는 스택을 사용한다.

https://gmlwjd9405.github.io/2018/08/14/algorithm-dfs.html

재귀 방법

시작 노드(a)를 방문했다고 표시하며 시작한다.
a와 인접한 노드들을 순회할 것인데,,!
a와 인접한 노드인 b에 인접한 노드가 있다면 b의 인접한 노드부터 돈다.

b를 새로운 시작노드로 선정하여 순회한다.
b의 인접한 노드를 모두 순회하면 a의 다음 인접노드를 순회한다.
모든 노드가 방문이 될 때까지 반복한다.

스택 방법

스택에 시작노드를 넣어주고 방문했다고 표시하며 시작한다.
스택의 맨 위를 선택하여 방문했는지 확인한다.

방문하지 않았다면 스택에 넣어준다.
스택의 맨 위의 값과 인접한 값들을 스택에 넣어준다. ( 방문했다면 넣지 않음)
스택이 빌 때까지 2~3을 반복한다.

/** graph의 형태 
[[], [1번과 인접한 정점], [2번과 인접한 정점..], .... ]
**/

fun dfs(graph : Array<MutableList<Int>>,size : Int,start : Int){
    val visited = Array(size+1){false}
    val stack = mutableListOf<Int>()

    graph.forEach { it.sortDescending() } // 스택은 위에서부터 꺼내기 때문에 큰 숫자부터 넣어주어야 한다.

    stack.add(start) // 초기정점 스택에 넣어주기
    print("$start ")
    visited[start] = true // 초기 정점은 자동으로 방문

    while (stack.isNotEmpty()){ // 스택이 빌때까지 반복.
        val top = stack.removeLast() // pop!!!
        if (!visited[top]){ // 현재 top이 방문했는지 확인
            print("$top ")
            visited[top] = true
        }
        graph[top].forEach { //현재 top과 인접한 얘들 반복
            if (!visited[it]) {
                stack.add(it)
            }
        }
    }
}