[알고리즘] 수행시간 분석

바람직한 알고리즘

1. 명확해야 한다.
   • 이해하기 쉽고 가능하면 간명하도록
   • 지나칙 기호적 표현은 오히려 명확성을 떨어뜨림
   • 명확성을 해치지 않으면 일반언어의 사용도 무방
2. 효율적이어야 한다.
   • 같은 문제를 해결하는 알고리즘들의 수행 시간이 수백만 배 이상 차이날 수 있다.

알고리즘의 수행시간

- 수행 시간 그래프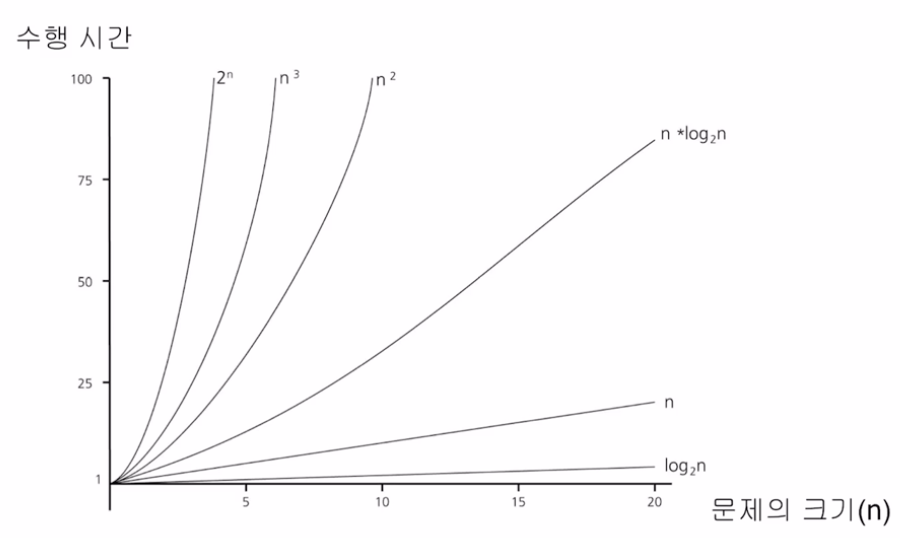

$2^n > n^3 > n^2 > nlog_2n > n > log_2n$의 수행시간을 가진다.
(수행시간이 짧을수록 좋은 성능의 알고리즘이라고 평가)

알고리즘의 수행 시간을 좌우하는 기준은 다양하게 잡을 수 있다.

예) for 루프의 반복횟수, 특정한 행이 수행되는 횟수, 함수의 호출횟수, ...!

sample1(A[ ], n){
	k = floor(n/2); // 바닥함수
    return A[k];
}

• n에 관계없이 상수 시간이 소요된다.

---

sample2(A[ ], n){
	sum = 0;
    for i=1 to n
    	sum = sum + A[i];
    return sum;

• n에 비례하는 시간이 소요된다.

---

sample3(A[ ], n){
	sum = 0;
    for i=1 to n
    	for j=1 to n
        	sum = sum + A[i]*A[j];
        return sum;

• $n^2$에 비례하는 시간이 소요된다.

---

sample4(A[ ], n){
	sum = 0;
    for i=1 to n
    	for j=1 to n {
        	k=A[1...n]에서 임의로 floor(n/2)개를 뽑을 때 이들 중 최댓값 ;
            sum = sum+k;
        }
    return sum;

• $n^3$에 비례하는 시간이 소요된다.

---

sample5(A[ ], n) {
	sum = 0;
    for i=1 to n-1
    	for j=i+1 to n
        	sum = sum + A[i]*A[j];
    return sum;
}

• $n^2$에 비례하는 시간이 소요된다.

i	부터~까지	반복 횟수
i=1	2~n	n-1번 반복
i=2	3~n	n-2번 반복
i=3	4~n	n-3번 반복
i=n-1	n-1~n	1번 반복

$sum_{i=1}^{n-1}(n-1) = sum_{i=1}^{n-1}i = 1/2(n)(n-1) => n^2$

---

factorial(n) {
	if (n=1) return 1;
    return n*factorial(n-1);
}

• n에 비례하는 시간이 소요된다.

factorial()이 호출되는 것이 시간을 좌우

---