렌더링 파이프라인에서의 기본적인 용어는 앞서 정리한 transformation, clipping, projection, rasterization이다.
transformation은 3차원 공간에 물체를 위치시키는 것이다. 공간은 3차원상이고, 형태는 아날로그 타입니다. clipping은 말 그대로 관측 공간 밖의 불필요한 부분을 제거하는 것이고, 공간은 역시 3차원상에 해당하고, 아날로그 형태로 나타난다. projection은 카메라 렌즈에 해당하고, 3차원을 2차원으로 가지고 오는 것이다. 차원은 2차원이고, 결과물은 아날로그 타입이다. 마지막으로 rasterization이라고 하는, 래스터화 과정을 거치게 되면 아날로그가 디지털로 바뀌게 된다. 즉 픽셀 형태의 디스플레이 장치로 나타내 준다.
모델링은 물체를 어떻게 설명하고 묘사할 것인지를, 렌더링은 만들어진 가상의 물체를 어떻게 실제처럼 보이게 할 것인지를 고민한다.
정육면체를 모델링하려면 어떻게 해야 할까? 먼저 중심점의 좌표가 원점 (0, 0, 0)이라고 가정한다. 그 다음 8개의 정육면체 꼭지점을 설정한다. 해당 점은 3차원 배열에 저장한다.
A: ( 1, 1, 1) E: ( 1, 1, -1)
B: (-1, 1, 1) F: (-1, 1, -1)
C: ( 1, -1, 1) G: ( 1, -1, -1)
D: (-1, -1, 1) H: (-1, -1, -1)점을 찍었다면 그 점을 이어 준다. 다음과 같은 총 12개의 선분에 관한 정보 역시 자료구조로 가지고 있어야 한다.
AB, CD, EF, GH,
AC, BD, EG, FH,
AE, CG, BF, DH그렇다면 3차원 정육면체를 어떻게 2차원 이미지로 그릴 수 있을까? 기본적인 전략은 먼저 3차원상에 찍힌 점을 2차원으로 매핑하는, 투영 과정을 거치는 것이다. 그 다음 2차원 상으로 옮겨진 점을 연결하는 과정을 거친다. 이때 저장해 둔 선분 정보를 사용한다.
Projection에는 Perspective projection과 Orthographic projection이 있다. 먼저 Perspective projection 즉, 투시법에 대해 알아보겠다.
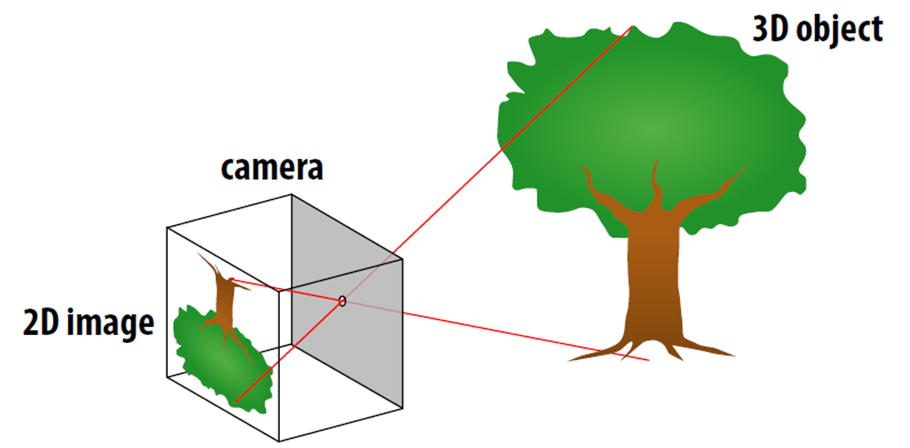
멀리 있는 물체는 작게 보이는, 원근법이 적용된 투영이다. 주로 3D를 다룰 때 사용한다. 위의 이미지를 옆에서 바라보면 다음과 같다.
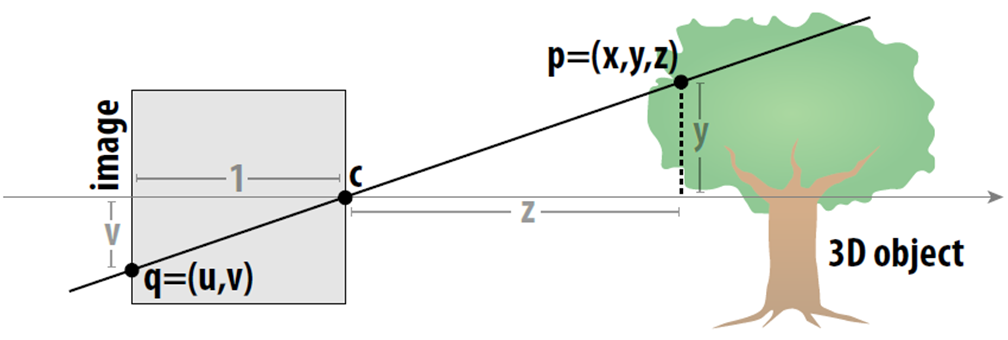
x, y, z 값으로 표현되는 점 p가 있다. 이 점을 2차원 이미지 상의 어떤 점에 대응시킬 수 있을까? 즉, 어떤 점에 매핑할 수 있을까? 해당 점을 q라고 한다면, q는 2차원 상의 점이므로 (u, v)로 표현할 수 있다. 위의 그림을 보면 두 개의 닮은 삼각형이 그려진다.
닮음비로부터 , 를 도출할 수 있다.
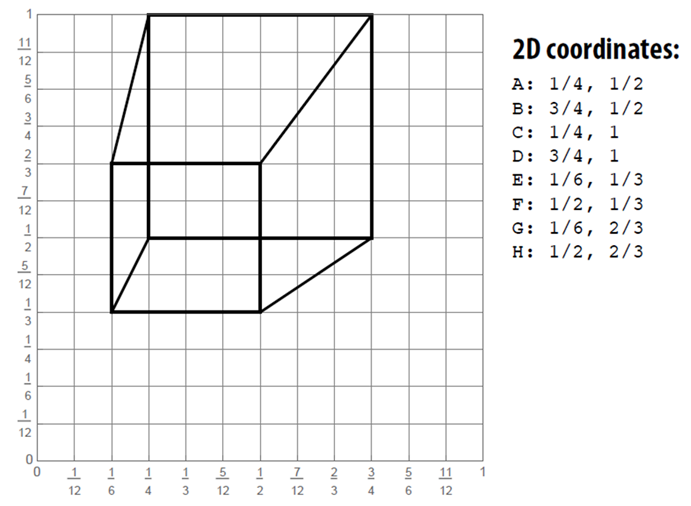
해당 과정을 통하여 모눈종이에 그림을 그린다면 위와 같은 그림이 그려질 것이다. 하지만 우리는 모눈종이에 그림을 그리는 것이 아니라 컴퓨터에 그림을 그려야 한다.
일반적인 raster 디스플레이는 이미지를 픽셀 형태의 2D grid 타입으로 표현한다. 각각의 픽셀마다 하나의 색을 부여한다. 일반적인 디스플레이를 확대해서 본다면 각 픽셀마다 R, G, B 색으로 이루어져 있는 것을 알 수 있다.
픽셀상에서 선을 그리려면 픽셀의 어떤 칸에 색칠을 해야 할까? 깔끔하게 일직선을 그릴 수 있다면 좋겠지만, 최종적인 결과물은 픽셀 형태로 표현하게 된다. 이러한 고민을 하는 작업을 Rasterization이라고 한다.
만약 선분이 지나가는 모든 픽셀을 색칠한다면 다음과 같은 결과물을 얻을 수 있을 것이다.
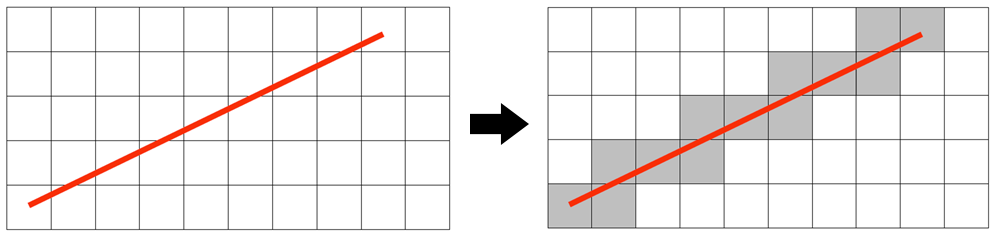
하지만 위 이미지는 '선'으로 보기에 부적합하다. 조금 더 자연스럽게 표현하기 위해 Diamond rule을 적용한다. 한 픽셀을 사각형으로 보는 것이 아니라, 내부를 채우는 다이아몬드로 보고, 그 다이아몬드에 교차하는 픽셀만 색칠하는 것이다.
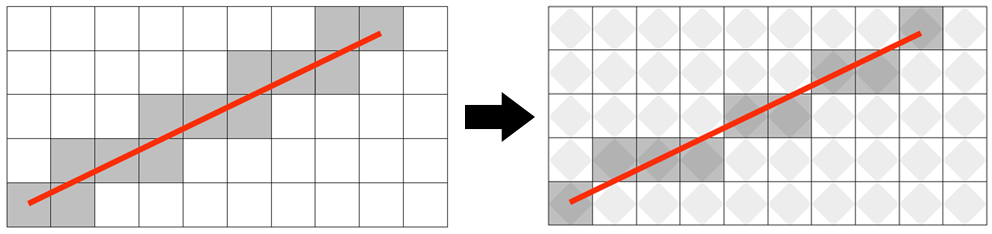
단순히 교차하는 모든 픽셀을 색칠한 좌측 이미지보다 다이아몬드 룰을 적용한 우측 이미지가 훨씬 자연스럽다.
이 과정을 조금 더 빠르고 편하게 사용하기 위해 적용하는 알고리즘이 Incremental line rasterization이다.
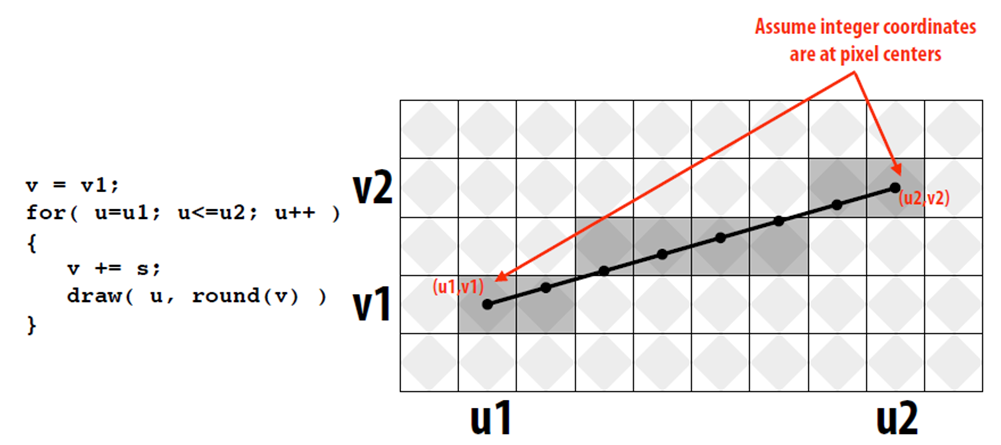
하나의 픽셀을 옮겨갈 때마다 연관된 픽셀들 중에서 하나의 픽셀만 칠할 수 있다. x의 값은 한 칸씩 옮겨가는 것이므로 +1만큼 커질 것이다. 반면 y값은 직선의 기울기가 s라면 기존의 값에서 s만큼 늘어날 것이다. 즉, v+s를 정수화한 값이 y값이 된다.
문제점은 v값에 실수 값이 존재할 수 있다는 것이다. 픽셀은 정수 값이므로, 오차가 발생할 수 있다.
따라서 Brsengam algorithm을 사용한다. 해당 알고리즘을 사용하게 되면 단순하게 정수들의 연산만을 사용해서 더 쉽게 다이아몬드를 그릴 수 있다.
