https://www.acmicpc.net/problem/9934
(전위 순회)
1. 가장 처음에 상근이는 트리의 루트에 있는 빌딩 앞에 서있다.
2. 현재 빌딩의 왼쪽 자식에 있는 빌딩에 아직 들어가지 않았다면, 왼쪽 자식으로 이동한다.
3. 현재 있는 노드가 왼쪽 자식을 가지고 있지 않거나 왼쪽 자식에 있는 빌딩을 이미 들어갔다면, 현재 노드에 있는 빌딩을 들어가고 종이에 번호를 적는다.
4. 현재 빌딩을 이미 들어갔다 온 상태이고, 오른쪽 자식을 가지고 있는 경우에는 오른쪽 자식으로 이동한다.
5. 현재 빌딩과 왼쪽, 오른쪽 자식에 있는 빌딩을 모두 방문했다면, 부모 노드로 이동한다.
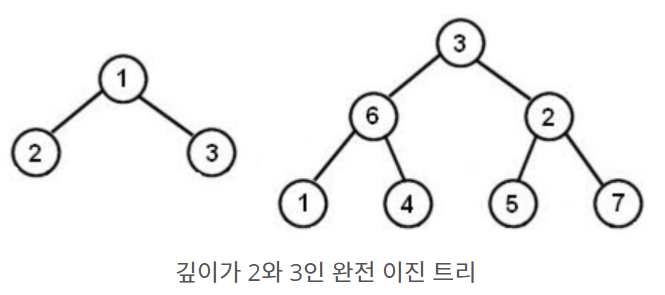
예제 입력 1
2
2 1 3
예제 출력 1
1
2 3
예제 입력 2
3
1 6 4 3 5 2 7
예제 출력 2
3
6 2
1 4 5 7
! 코드, 풀이 해설을 보기 전 고민하는 시간을 충분히 가져보세요!
# 9934 완전 이진 트리
K = int(input())
numbers = list(map(int, input().split()))
tree = [[] for _ in range(K)]
for idx, number in enumerate(numbers):
num = 2 ** 10
cnt = 10
while (idx + 1) % num != 0:
cnt -= 1
num //= 2
tree[cnt].append(number)
for i in range(len(tree) - 1, -1, -1):
print(' '.join(map(str, tree[i])))

풀이 해설
숫자 순서를 담은 numbers 배열을, for문과 enumerate를 통해 하나씩 가져온다.
idx는 numbers의 몇 번째 숫자(순서)를 가져왔는지를 나타낸다.
idx == 순서 (엄밀히 말하면 idx + 1)
number == 현재 들고 있는 숫자.
tree == 숫자를 배치할 트리. 이중 리스트로 트리의 층수 표현.
난 지금 number 하나를 들고 있다. 이제 무엇을 할 것인가?
트리 K개를 만든 뒤, 아래 층부터 채워가는 알고리즘을 생각해보자.
트리를 채우기 위해, 트리의 어느 부분에 내가 들고 있는 숫자 number를 채울 것인지를 생각해야 한다.
예제 2에서 숫자가 들어간 규칙을 살펴보면
예제 입력 1 6 4 3 5 2 7
트리 층수 1 2 1 3 1 2 1
-
맨 아래쪽의 1, 4, 5, 7은 한 칸 건너 나타나는 형태임을 알 수 있다.
즉, 지금 맨 아래 트리에 숫자를 채웠다면, 그 다음 번엔 위에 있는 어떤 트리의 숫자를 추가할 것이고,
위의 트리에서 숫자를 채웠다면, 그 다음 번엔 맨 아래에 있는 트리의 숫자를 추가할 것이다. -
트리 층수에서 1, 2, 1이 반복적으로 나타난다.
중간에 나타난 3도 같은 형태이다. 1, 2, 1을 11로 치환해보자.
그렇다면 1, 2, 1, 3, 1, 2, 1은 11, 3, 11과 같이 표현할 수 있다.
혼자서 숫자를 반복해서 써가보면서, 어떤 규칙성을 찾아냈다.
- 4의 배수인 순서에서 3 이상의 값을 갖는다.
- 그 사이엔 1, 2, 1이 들어간다.
- 1, 2, 1, 3, 1, 2, 1 뒤에 4 라는 새로운 트리 층수가 나타난다.
- 4뿐만 아니라 앞으로 5, 6, 7... 등이 순차적으로 등장할 것임을 예측할 수 있다. - 홀수 번째
규칙성을 찬찬히 찾아보고 코드를 작성해가면서(코드로 답을 끼워맞춰가면서) 추가적인 규칙성을 발견했다.
- 4번째 순서에 3이, 8번째 순서에 4가, 16번째 순서에 5가 나온다.
- 주어진 조건에서, 완전이진트리를 가정했기 때문이다. - 2^(n-1)번째 순서에 = n이 나온다. 로 일반화를 할 수 있었다.
- 그렇다면 12번째 처럼 애매한 순서는?- 12 = 3 * 4 이므로, 4(2^2)의 배수니까 3이 나올 것이라고 가정할 수 있다.
위와 같은 일반화 과정을 거쳤고, 코드로 구현했다.
num = 2 ** 10
K는 10 이하이므로 제일 큰 num은 2^10이다.
cnt = 10
몇 번째 tree 값을 고를지 알려주는 변수이다.
while (idx + 1) % num != 0:
idx는 0부터 시작하고, 난 첫 번째 숫자가 1이길 원하므로 1을 더해줬다.
내가 들고 있는 숫자의 순서(idx + 1)와 num의 나머지를 구했을 때, 0이면(idx + 1이 num의 약수이면) while문을 탈출한다.
약수가 아니라면 다음 과정을 반복한다.
cnt -= 1
num //= 2
트리 층수를 한 층 낮추고,
num은 2로 나눠준다.
tree[cnt].append(number)
cnt 층에 현재 들고 있는 number를 추가해준다.
for i in range(len(tree) - 1, -1, -1):
맨 위층부터 출력을 해줘야 한다. (그래야 맨 마지막 출력이 맨 아래층이다.)
그냥 for문을 걸면, i=0부터 시작하므로, 맨 위층부터 출력하도록 만들었다.
print(' '.join(map(str, tree[i])))
list 형태인 tree[i]를 이쁘게 출력한다.