기초수학(파이썬)_11일차_학습일지

📝 정리

수열이란?
규칙성을 가지고 나열되어 있는 수들

1. 등차수열

연속된 두 항의 차이가 일정한 수열

일반항(an) : 규칙성을 갖고있는 수들을 구할 수 있는 식
공차(d) : n과 n+1 사이에 차이
등차중앙 : 연속된 세 항에서 가운데항

등차수열의 합

일반항
an = a1+(n-1)*d
등차수열의 합
sn = n(첫번째항 +마지막항) / 2

<파이썬의 대입하여 사용 시>
마지막항은 an 공식을 써서 넣음.

2. 등비수열
연속된 두 항의 비(곱으로 커짐)가 일정한 수열

공비(r) :일정하게 커지는 비
등비 중항 : 중간에 있는 숫자 2제곱 = 양옆 숫자 곱한것

일반항
an = a1 * r^(n-1)
<코드변환>
an = a1 * (r ** (n-1))

등비수열의 합
sn = a1 * (1 - (r^n) / (1-r)
<코드변환>
sn = a1 * ( 1- r ** n) / (1-r)

3. 계차 수열

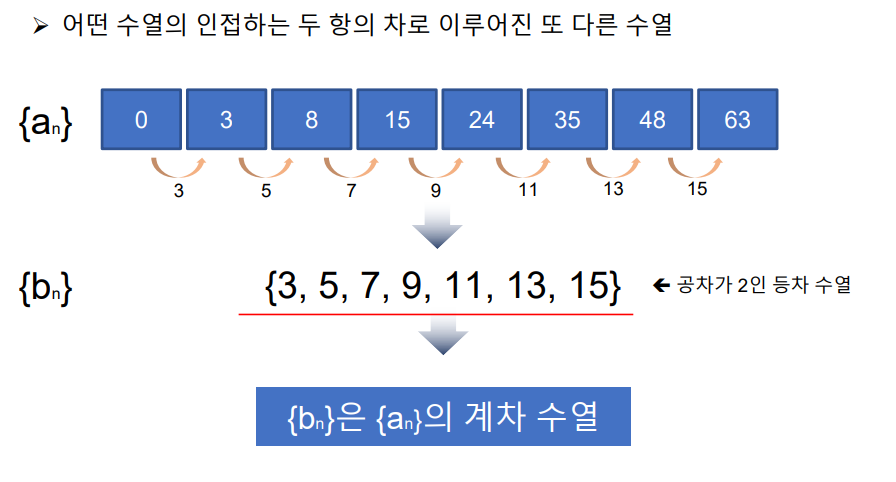
계차수열의 합
bk = an - a1

n-1
∑ bk = an - a1
k=1

4. 팩토리얼

1부터 양의 정수 n까지의 정수를 모두 곱한 것

파이썬으로 구하는 방법 3

1) for문

inputN = int(input('n 입력: '))

result = 1
for i in range(1, (inputN+1)):
    result *= i

2) 재귀함수

inputN = int(input('n 입력: '))

def factorialFun(n):
    if n == 1: return 1

    return n * factorialFun(n-1)

3) math 모듈

inputN = int(input('n 입력: '))

import math
print('{}팩토리얼: {}'.format(inputN,math.factorial(inputN)))

👀 다시보기

피보나치수열

등차수열에서 조건 몇가지만 추가되면 피보나치 수열이 된다!

조건1)
a1 = 1
a2 = 1
a3 = a1 + 2 이다.

조건2)
an = an-2+ an-1

if n == 1 or n == 2:
	valueN = 1
    valuePreN2 = valueN
    valuePreN1 = valueN
    sumN += valueN
    n += 1

나머지도
valueN += inputD 였던 것과 달리

else:
   valueN = valuePreN1 + valuePreN2
   valuePreN2 = valuePreN1
   valuePreN1 = valueN

💬 코멘트

파이썬이 아무래도 수학처리가 되는 프로그래밍이다보니
이런 기초수학의 대한 이해가 되어있으면 정말 많은 활용이 가능한 프로그래밍 같다.
코드가 무척 직관적이고 쉬워서 보다보면 작성자인 내가 오히려 수학에 대한 밑바탕이 되었으면 간단히 나왔을 문제들이여서...😅
내일도 화이팅👉