인공신경망(feat.퍼셉트론)

퍼셉트론은 뉴런을 모방해서 만든 알고리즘.

퍼셉트론은 X = [x1, x2, ...] 가 인풋일 때 y를 아웃풋으로 가짐

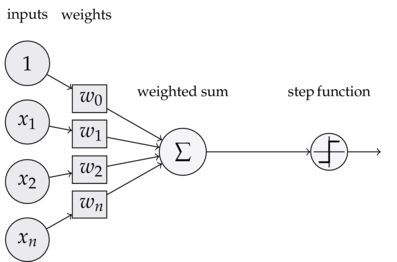
y = 0 (WX <= ⍬) or 1 (WX > ⍬), where ⍬ = threshold

위 식을 재정립 하면,

y = 0 (WX + b <= 0) or 1 (WX + b > 0), where b = bias

#AND Perceptron
import numpy as np

def AND(x1, x2):
  X = np.array([x1, x2])
  W = np.array([0.5, 0.5])
  b = -0.5
  theta = 0.5
  y = np.sum(X * W) + b
  if y <= 0:
    return 0
  elif y > 0:
    return 1
  
print(AND(1,1)) #1
print(AND(1,0)) #0
print(AND(0,1)) #0
print(AND(0,0)) #0

#OR Perceptron
import numpy as np

def OR(x1, x2):
  X = np.array([x1, x2])
  W = np.array([0.5, 0.5])
  b = -0.4
  y = np.sum(X * W) + b
  if y <= 0:
    return 0
  elif y > 0:
    return 1

print(OR(1,1)) #1
print(OR(1,0)) #1
print(OR(0,1)) #1
print(OR(0,0)) #0

#NAND Perceptron
import numpy as np

def NAND(x1, x2):
  X = np.array([x1, x2])
  W = np.array([-0.5, -0.5])
  b = 0.6
  y = np.sum(X * W) + b
  if y <= 0:
    return 0
  elif y > 0:
    return 1

print(NAND(1,1)) #0
print(NAND(1,0)) #1
print(NAND(0,1)) #1
print(NAND(0,0)) #1

그러나 single layer perceptron은 XOR을 분류 할 수 없다는 치명적인 단점이 있다.

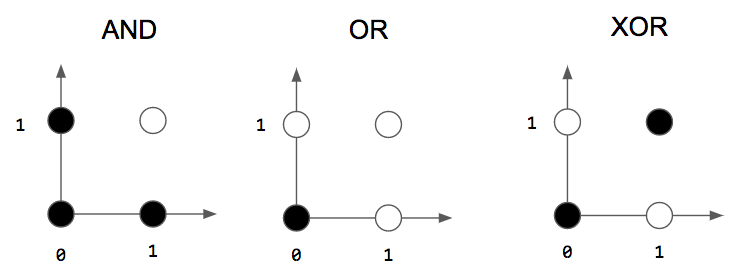
이를 개선한 것이 multi layer perceptron이다.

import numpy as np

def NOR(x1, x2):
  s1 = NAND(x1, x2)
  s2 = OR(x1, x2)
  y = AND(s1, s2)
  return y

print(NOR(1,1)) #0
print(NOR(1,0)) #1
print(NOR(0,1)) #1
print(NOR(0,0)) #0

...사실 NAND 게이트로 모든 논리 표현이 가능. 즉, 컴퓨터 설계도 가능. 이론적으로 1개의 히든레이어를 가진 퍼셉트론으로도 비선형 시그모이드 함수를 활성화 함수로 사용하면 컴퓨터를 만들 수 있음.

복잡한 계산을 하기 위해선 W의 가중치를 실험적으로 적절히 배합해 줘야 함.

퍼셉트론은 활성화 함수로 step function 사용.
신경망은 활성화 함수로 시그모이드 함수, ReLU 등 사용.