[자료구조] 스택/큐/그래프 (feat.Python)

a.very·2021년 7월 10일

CS-Study

목록 보기

1/6

https://github.com/WeareSoft/tech-interview/blob/master/contents/datastructure.md 의 내용을 기반으로 작성하였습니다.

👾 Stack

개념

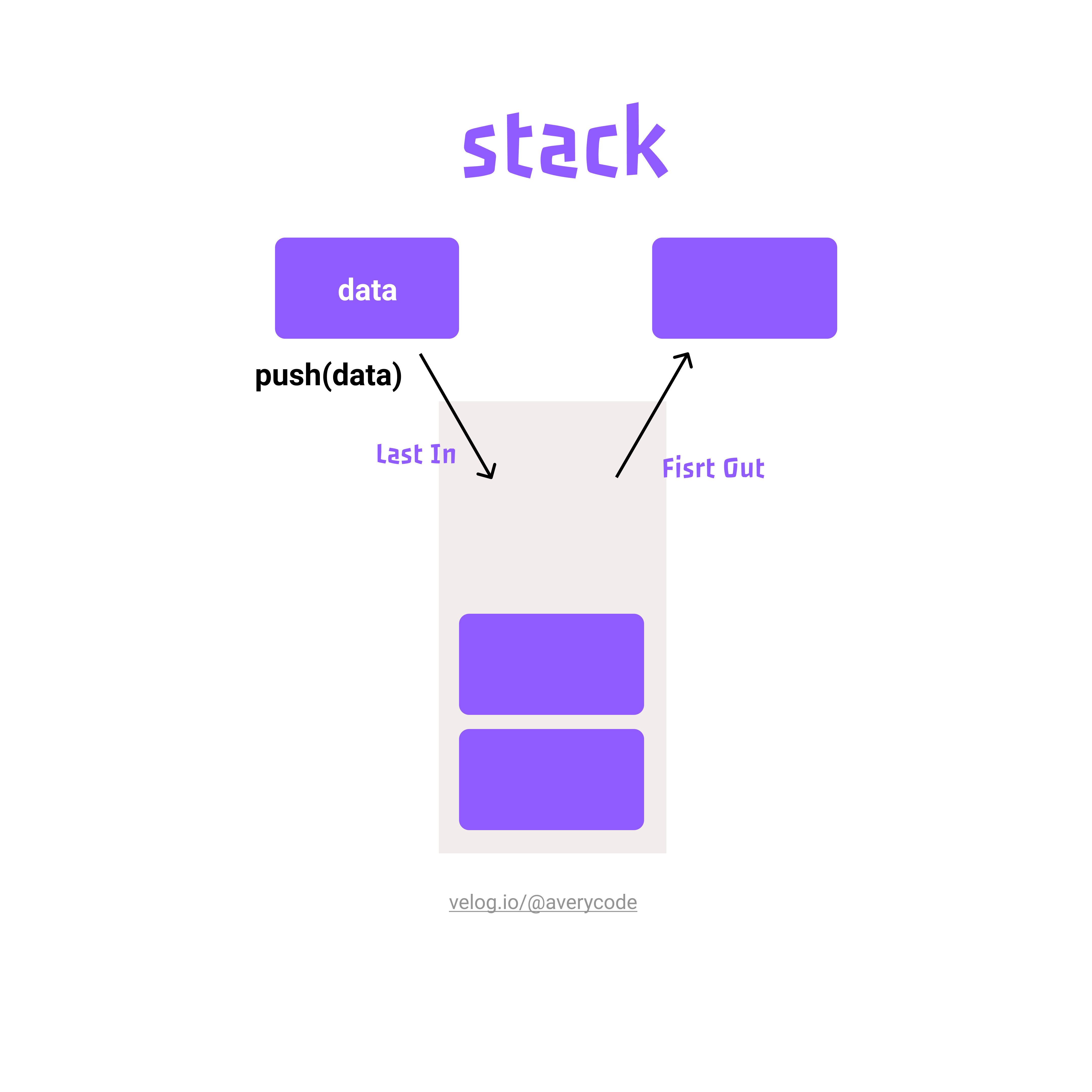
스택이란 한쪽 끝에서만 자료를 넣고 뺄 수 있는 선형구조(LIFO 특징)로 된 자료구조입니다.
스택_averycode

장점

구조가 단순해서, 구현이 쉽다.
데이터 저장/읽기 속도가 빠르다.

단점 (일반적인 스택 구현시)

데이터 최대 갯수를 미리 정해야 한다.
파이썬의 경우 재귀 함수는 1000번까지만 호출이 가능함
저장 공간의 낭비가 발생할 수 있음
미리 최대 갯수만큼 저장 공간을 확보해야 함

스택의 연산

LIFO(LAST IN FIRST OUT)한 특징을 가지는 스택의 연산은 다음과 같습니다.

pop() : 스택의 가장 위(peek)에 있는 항목 제거
push(data) : data 하나를 스택의 가장 위(peek)에 추가
peek() : 스택의 가장 위에 있는 항목 return
isEmpty(): 스택이 비어있을때, true를 return

스택의 활용사례

재귀알고리즘에 유용
- 재귀적으로 함수를 호출해야 하는 경우에 임시 데이터를 스택에 넣어준다.
- 재귀함수를 빠져 나와 퇴각 검색(backtrack)을 할 때는 스택에 넣어 두었던 임시 데이터를 빼 줘야 한다.
- 스택은 이런 일련의 행위를 직관적으로 가능하게 해 준다.
- 또한 스택은 재귀 알고리즘을 반복적 형태(iterative)를 통해서 구현할 수 있게 해준다.
웹 브라우저 방문기록
실행 취소 (undo)
역순 문자열 만들기
수식의 괄호 검사
후위 표기법 계산

스택을 파이썬에서 사용해보기 :)

파이썬의 list타입을 이용하여 스택사용하기

stack = []
stack.push(4) # [4]
stack.push(6) # [4,6]
stack.push(7) # [4,6,7]
print(stack[-1])  # 7
print(stack.pop()) #7 [4,6]

파이썬의 deque라이브러리 를 이용하여 스택사용하기 (큐를 만들때도 활용이 가능하다)

아래의 Dequeue에서 자세히 설명하겠다.

👾 Queue

개념

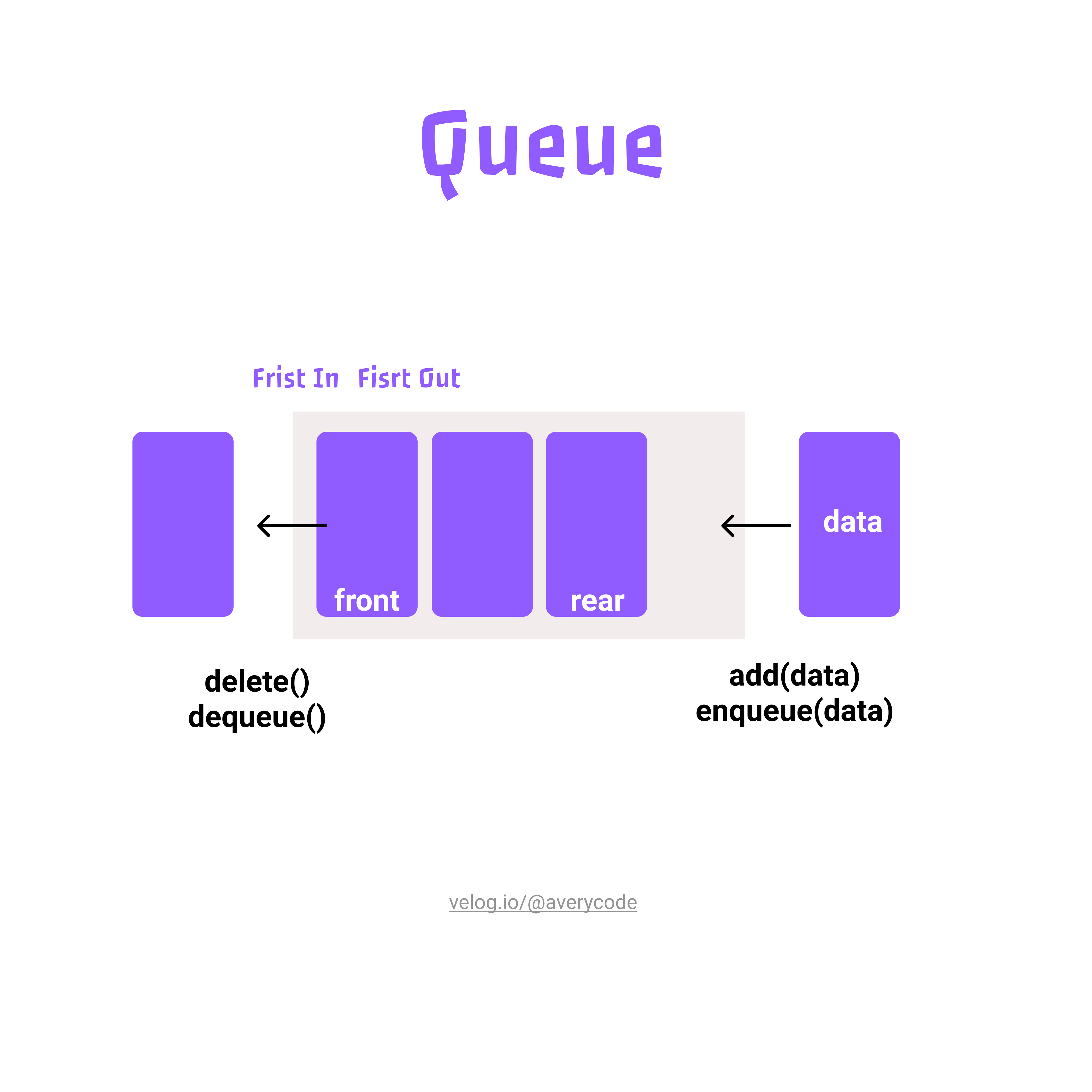
컴퓨터의 기본적인 자료 구조의 한가지로, 먼저 집어 넣은 데이터가 먼저 나오는 FIFO(First In First Out)구조로 저장하는 형식이다.
queue_averycode

큐의 연산

FIFO(First-In-First-Out)의 규칙을 따르는 큐의 연산은 다음과 같이 대표됩니다.

add(item): item을 리스트의 끝부분에 추가
remove(): 리스트의 첫 번째 항목을 제거
peek() : 큐의 가장 위에 있는 항목 return
isEmpty(): 큐가 비어있을때, true를 return

큐의 활용

데이터가 입력된 시간 순서대로 처리해야 할 필요가 있는 상황에 이용한다.

너비 우선 탐색(BFS, Breadth-First Search) 구현
처리해야 할 노드의 리스트를 저장하는 용도로 큐(Queue)를 사용한다.
노드를 하나 처리할 때마다 해당 노드와 인접한 노드들을 큐에 다시 저장한다.
노드를 접근한 순서대로 처리할 수 있다.
캐시(Cache) 구현
우선순위가 같은 작업 예약 (인쇄 대기열)
선입선출이 필요한 대기열 (티켓 카운터)
콜센터 고객 대기시간
프린터의 출력 처리
윈도우 시스템의 메시지 처리기
프로세스 관리

큐의 종류

1. Linear Queue (선형큐)

막대 모양으로 된 큐
크기가 제한적
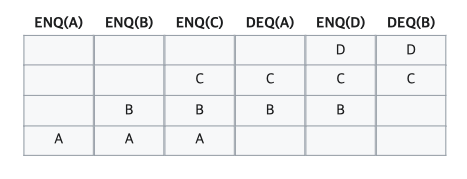
(단점)빈 공간을 사용하려면 모든 자료를 꺼내거나 자료를 한 칸씩 옮겨야 한다. 다음은 선형 큐의 작동 방식이다.
DATA : A B C D E

2. Circular Queue (원형큐)

원형큐/ 환형큐
선형 큐의 문제점(배열로 큐를 선언할시 큐의 삭제와 생성이 계속 일어났을때, 마지막 배열에 도달후 실제로는 데이터공간이 남아있지만 오버플로우가 발생)을 보완한 것
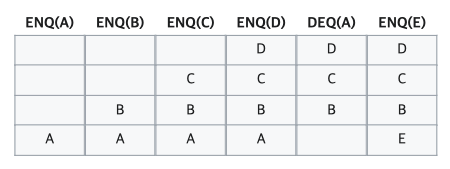
front가 큐의 끝에 닿으면 큐의 맨 앞으로 자료를 보내어 원형으로 연결 하는 방식이다.

다음은 원형 큐의 작동 방식이다.
DATA : A B C D E

3. Linked List Queue (연결리스트를 이용해 구현한 큐)

연결 리스트로 구현한 큐는 연결 리스트를 사용하여 만듬
큐의 길이를 쉽게 늘릴 수 있어 오버플로우가 발생하지 않는 것이 특징이다.
필요에 따라 환형으로 만들 수도 있으며, 환형으로 만들지 않아도 삽입과 삭제가 제한되지 않아 편리하다.

큐를 파이썬에서 사용해보기 :)

파이썬의 queue라이브러리를 이용하여 큐 만들어쓰기

from queueimport Queue
q = queue() # 빈큐 생성
q.put(1) # add(원소)
q.put(2)
q.put(3)
q.put(4)
q.get() # 4

파이썬의 deque라이브러리 를 이용하여 큐사용하기

아래의 Dequeue에서 자세히 설명하겠다.

👾 Dequeue

스택과 큐를 합친 자료구조로 앞뒤에 원소를 넣고 뺄 수 있다.

from collections import deque

dq=deque()  
dq.append() # push
dq.pop() # pop 5
dq.popleft() # 가장 왼쪽 원소 반환
dq.appendleft() # 덱의 가장 왼쪽에 원소 삽입
dp.pop() # 가장 오른쪽 원소 반환
dp.clear() # 모든 원소 제거
dp.copy() # 덱 복사
dp.count(x) #x와 같은 원소의 개수를 계산

deque(iterable, [, maxlen]) : 초기화 함수로, iterable(리스트 등)을 인자로 건내면 이를 deque화 시켜준다.

from collections import deque

dq1 = deque() #빈큐

dq2 = deque([1, 2, 3, 4, 5])

# 큐 최대 길이 명시하기(원소를 이보다 많이 넣으면 maxlen이 자동 갱신됨)
dq3 = deque(maxlen=5)

👾 Graph

개념

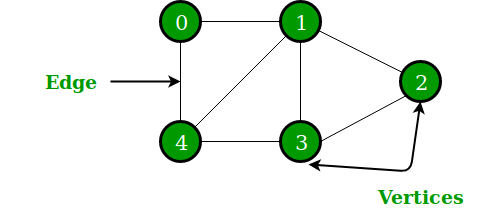
그래프는 노드(N, node)와 그 노드들을 연결하는 엣지(E, edge)를 포함하는 비선형 자료구조입니다. 즉, 연결되어있는 객체 관의 관계를 표현할 수 있습니다.

Ex) 지도, 지하철 노선도의 최단 경로, 전기 회로의 소자들, 도로(교차점과 일방 통행길), 선수 과목 등
그래프는 여러 개의 고립된 부분 그래프(Isolated Subgraphs)로 구성될 수 있다.

A Graph consists of a finite set of vertices(or nodes) and set of Edges which connect a pair of nodes. - geeksforgeeks

geeksforgeeks

그래프의 특징

그래프는 네트워크 모델 이다.
2개 이상의 경로가 가능하다.
- 즉, 노드들 사이에 무방향/방향에서 양방향 경로를 가질 수 있다.
self-loop 뿐 아니라 loop/circuit 모두 가능하다.
루트 노드라는 개념이 없다.
부모-자식 관계라는 개념이 없다.
순회는 DFS나 BFS로 이루어진다.
그래프는 순환(Cyclic) 혹은 비순환(Acyclic)이다.
그래프는 크게 방향 그래프와 무방향 그래프가 있다.
간선의 유무는 그래프에 따라 다르다.

그래프의 종류

그래프의 종류는 크게 세가지로 나뉜다.
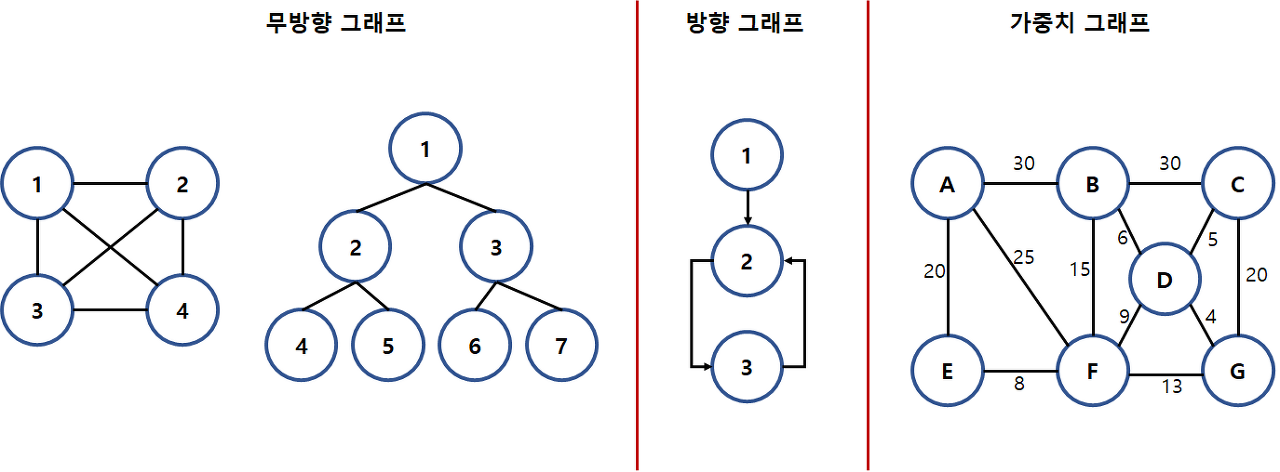
1. 무방향 그래프(Undirected Graph)

간선을 통해서 양방향으로 갈 수 있다.
(A,B) = (B,A)

2. 방향그래프 (Directed Graph)

간선에 방향성이 존재하여 해당 방향으로만 유효하다.
A -> B 는 <A,B>로 표기
<A,B> != <B,A>

3. 가중치 그래프 (Wighted Graph)

간선에 비용/가중치가 할당된 그래프이다.
네트워크 라고도 한다. (도시-도시의 연결, 도로의 길이, 회로 소자의 용량, 통신망 사용료 등)

👀 연결 (연결그래프 VS 비연결그래프)

그래프는 연결여부에 따라 두가지로 나뉠 수 있다.

연결 그래프(Connected Graph)

무방향 그래프에 있는 모든 정점쌍에 대해서 항상 경로가 존재하는 경우
Ex) 트리(Tree): 사이클을 가지지 않는 연결 그래프

비연결 그래프(Disconnected Graph)

무방향 그래프에서 특정 정점쌍 사이에 경로가 존재하지 않는 경우

👀 완전그래프

그래프에 속해 있는 모든 정점이 서로 연결되어 있는 그래프
무방향 완전 그래프
- 정점 수: n이면 간선의 수: n * (n-1) / 2

👀 사이클 (순환그래프 VS 비순환그래프)

사이클이란 단순 경로(경로중에서 반복되는 정점이 없는 경우)의 시작 점정과 종료정점이 동일한 경우이다.

비순환 그래프 : 사이클이 없는 그래프

아래의 간단한 예제를 통해 사이클에 대해 자세히 이해해보겠다.
우선 무방향그래프의 경우이다.

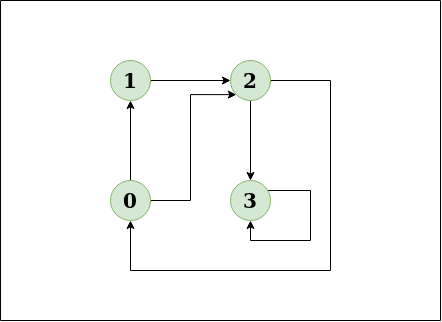
다음의 "무방향그래프"가 존재할때, 사이클이 존재하나요?
Input: n = 4, e = 4 
0 1, 1 2, 2 3, 0 2 
"YES" : 사이클은 0-2-1-0에서 존재한다.

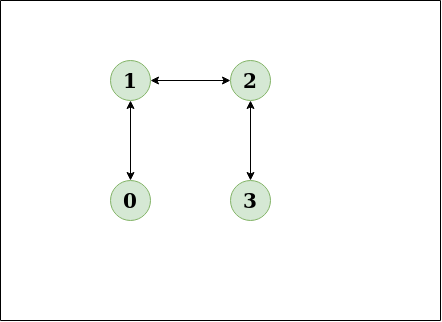
다음의 "무방향그래프"가 존재할때, 사이클이 존재하나요?
Input:n = 4, e = 3 
0 1, 1 2, 2 3 
"NO" : 시작정점과 종료정점이 동일한 경우는 존재하지 않는다.

다음은 방향그래프의 경우이다.
방향그래프에서는 화살표를 따라가다보면 사이클이 존재하는지 쉽게 확인가능하다.

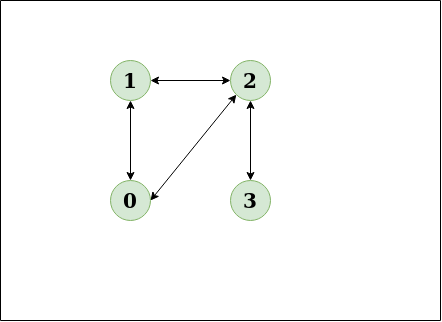
다음의 "방향그래프"가 존재할때, 사이클이 존재하나요?
Input: n = 4, e = 6
0 -> 1, 0 -> 2, 1 -> 2, 2 -> 0, 2 -> 3, 3 -> 3
"YES" : 0 - 2 - 0 에서 사이클이 보여진다. 2에서 0으로 연결되서 사이클이 발생한다.

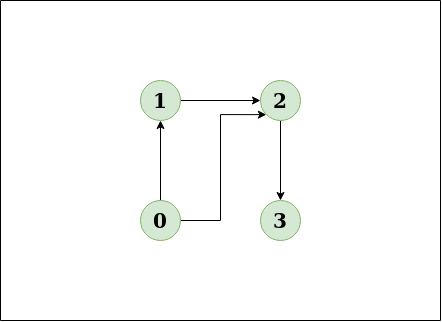
다음의 "방향그래프"가 존재할때, 사이클이 존재하나요?
Input:n = 4, e = 4
0 -> 1, 0 -> 2, 1 -> 2, 2 -> 3
"NO"

그래프의 탐색

그래프를 탐색하는 방법은 일반적으로 2가지로 이야기한다. 하지만 해당 부분은 나중에 자세히 설명하도록하겠다.

DFS (Depth-First-Search) : 깊이우선탐색
루트 노드(혹은 다른 임의의 노드)에서 시작해서 다음 분기(branch)로 넘어가기 전에 해당 분기를 완벽하게 탐색하는 방법
BFS (Breadth-First-Search) : 너비우선탐색
루트 노드(혹은 다른 임의의 노드)에서 시작해서 인접한 노드를 먼저 탐색하는 방법

👾 Visualisation

다음의 사이트들을 이용하며 더욱 자료구조를 이해하기 쉬울 것이다.
https://visualgo.net/en/list
https://www.cs.usfca.edu/~galles/visualization/StackLL.html

링크드리스트로 스택 구현

출처모음

https://ooeunz.tistory.com/31
https://ko.wikipedia.org/wiki/%ED%81%90_(%EC%9E%90%EB%A3%8C_%EA%B5%AC%EC%A1%B0)
https://docs.python.org/3.8/library/collections.html#collections.deque
https://velog.io/@yeseolee/Python-%EC%9E%90%EB%A3%8C%EA%B5%AC%EC%A1%B0-%EC%8A%A4%ED%83%9DStack
https://www.geeksforgeeks.org/graph-data-structure-and-algorithms/
https://visualgo.net/en/list
https://www.cs.usfca.edu/~galles/visualization/StackLL.html
https://pangtrue.tistory.com/147
https://gmlwjd9405.github.io/2018/08/13/data-structure-graph.html
https://velog.io/@inyong_pang/%ED%81%90Queue#4-%ED%94%84%EB%A1%9C%EA%B7%B8%EB%9E%98%EB%B0%8D-%EC%97%B0%EC%8A%B5

a.very

🚚chanhee-jeong.tistory.com 🚀 github.com/chaneeii/iOS-Study-Log