230314

완전 탐색

모든 경우의 수를 탐색하여 정답을 찾는 방법, Brute-Force 알고리즘이라고도 불린다.

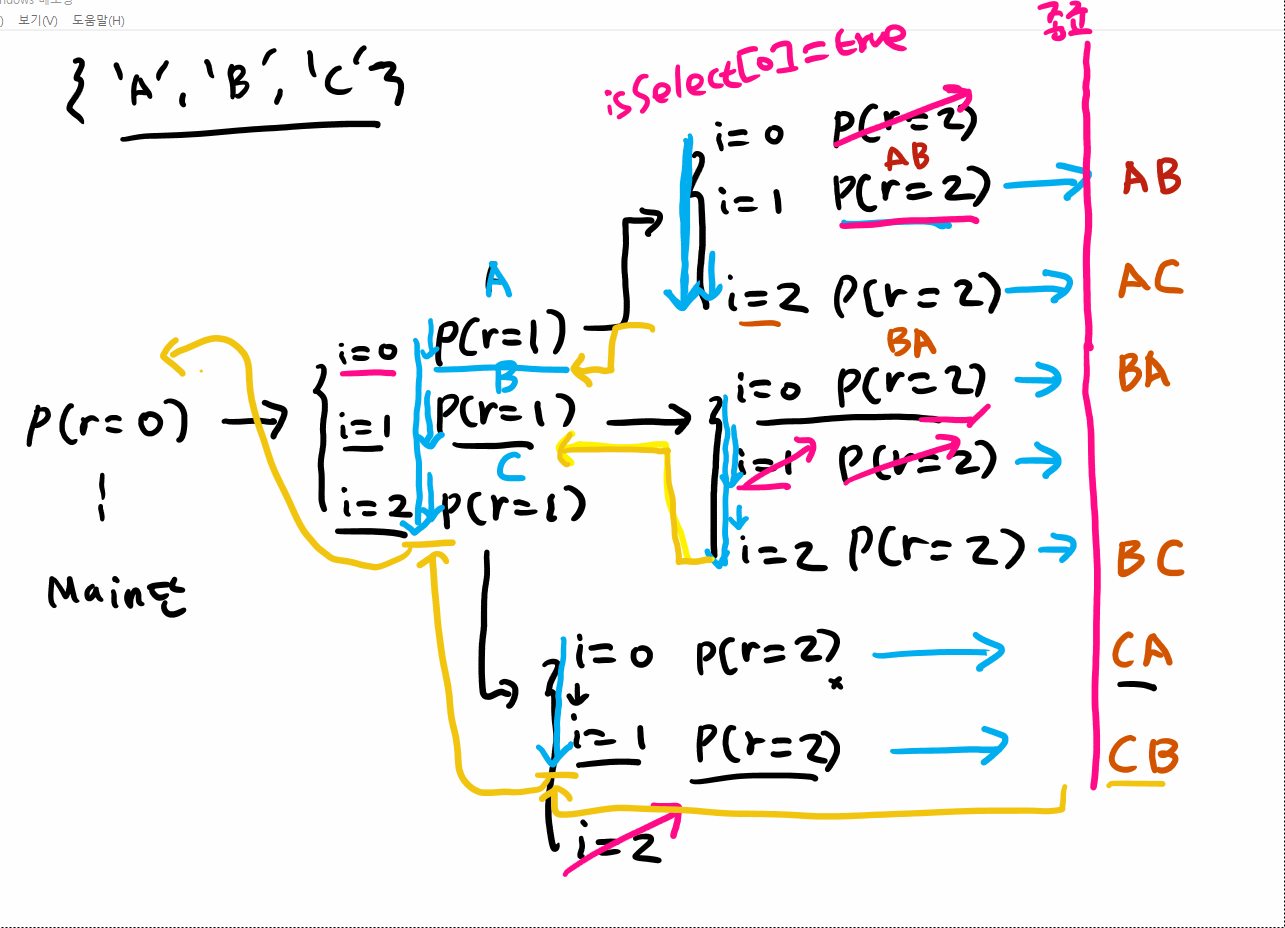
1. 순열 (n P r)

서로 다른 n개의 원소에서 중복을 허용하지 않고 r개를 순서대로 선택하는것 (순서가 있다)

public Class Recursive {
	static int R;
    static String [] arr = {'A', 'B', 'C', 'D'};
    // 인덱스를 기록할 배열
    static int [] selection = new int [R];
    // 선택 여부를 기록할 배열
    static boolean [] isSelected = new int [arr.length];
    
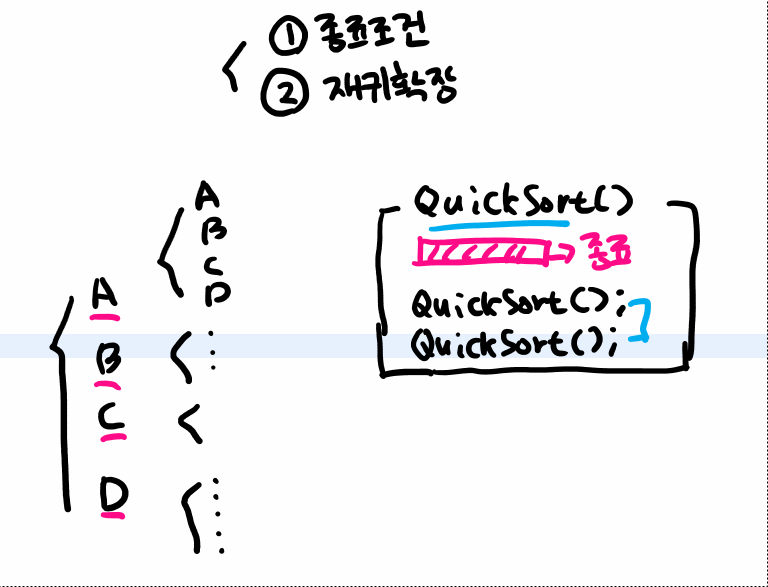
    public static void permutation(int r){
    	// r이 뽑는 숫자 R까지 도달한다면 멈춤
        if(r==R) {
        	for(int i=0; i<R; i++) System.out.print(arr[selection[i]]);
			System.out.println();
			return;
        }
        
        for(int i=0; i<arr.length; i++){
        	if(isSelected[i]) continue; // 이미 선택되었다면 패스
            isSelected[i] = true; // 선택 기록
        	selection[r] = i; // 인덱스 기록
            permutation(r+1); // 다음 순번을 기록하기 위한 재귀
            isSelected[i] = false; // 기록 해제 (백트래킹)
        }
        
    }
    
    public static void main(String[] args) {
		R = 2;
        permutation(0);
	}
    
	
}

2. 조합 (n C r)

서로 다른 n개의 원소에서 중복을 허용하지 않고 r개를 순서 없이 선택하는 것 (순서가 없다)

public Class Combination {
	static int R;
    static String [] arr = {'A', 'B', 'C', 'D'};
    static int [] selection = new int [R];
    static boolean [] isSelected = new int [arr.length];
    
    public static void combination(int r, int start){
    	if(r==R) {
        	for(int i=0; i<R; i++) System.out.print(arr[selection[i]]);
			System.out.println();
			return;
        }
        // 순열과 차이점은 start!
        // start를 이용해 순서를 없앤다.
        for(int i=start; i<arr.length; i++){
        	if(isSelected[i]) continue;
            isSelected[i] = true;
        	selection[r] = i;
            combination(r+1, i);
            isSelected[i] = false;
        }
        
    }
    
    public static void main(String[] args) {
		R = 2;
        combination(0,0);
	}
    
	
}

3. 부분집합

주어진 집합에서 일부 원소들로 구성된 집합을 만드는 것

package Day4;

public class Subset {
		
	static char [] arr;
	static int N;
	static boolean [] isSelected;
	static int cnt;
	
	static void subset(int num) {
		// 종료 조건
		if(num == N) {
			cnt++;
			for(int i=0; i<N; i++) {
				if(isSelected[i]) System.out.print(arr[i] + " ");
			}
			System.out.println();
			return;
		}
		
		// 분할
		// 선택 O
		isSelected[num] = true;
		subset(num+1);
		// 선택 X
		isSelected[num] = false;
		subset(num+1);
	}
	
	public static void main(String[] args) {
		arr = new char [] {'A', 'B', 'C', 'D'};
		N = arr.length;
		
		isSelected = new boolean[N];
		
		subset(0);
		System.out.println(cnt);
	}

}