230322
1. 유니온 파인드
두 노드가 같은 그래프에 속하는지 판별하는 알고리즘
- 서로소 집합, 상호 배타적 집합으로도 불림
- 트리 구조로 이루어진 자료
- 최소신장트리를 구하는 크루스칼 알고리즘에서 사용
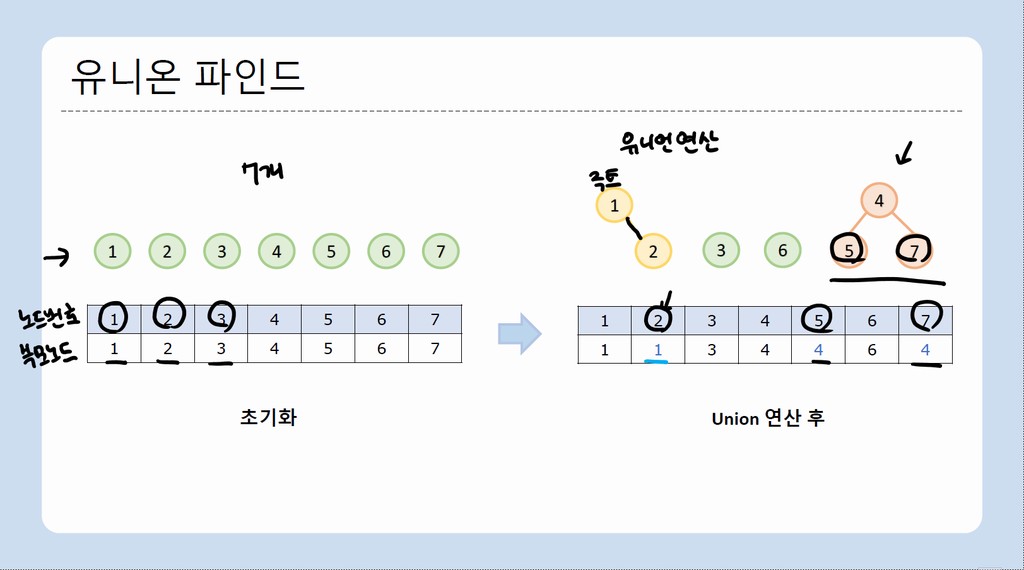
Find 연산
: 루트 노드를 찾는 연산
// 루트노드를 기록하는 배열 초기화
parent = new int [v+1];
Arrays.setAll(parent, (i) -> (i));
int find(int num){
// 자기 자신이 루트라면 리턴
if(num == parent[num]) return num;
// 자기 자신이 루트가 아니라면 재귀를 이용해 단계적으로 루트를 찾아감
return parent[num] = find(parent[num]);
}
Union 연산
: 두 노드를 합치는 연산
void union(int a, int b){
// 연결할 두 노드의 루트를 찾음
a = find(a);
b = find(b);
// 루트가 다르다면 더 큰 값의 루트배열값에 작은값 대입
if(a!=b){
if(a<b) parent[b] = a;
else parent[a] = b;
}
}
2. 최소신장트리
신장 트리
그래프 내 모든 정점을 포함하는 트리 (사이클을 돌지 않는다)
최소 신장 트리
신장 트리 중 간선들의 가중치 합이 최소인 트리
- N개 정점을 가지는 그래프에서 N-1개의 간선으로 연결된 형태
- 네트워크 분야에서 응용
3. 크루스칼 알고리즘
모든 정점을 최소 비용으로 연결하는 최소 신장 트리를 구하는 알고리즘
그리디 알고리즘을 이용해 최소의 비용이 드는 간선들부터 선택해가는 방식
- 그래프의 간선들을 가중치의 오름차순으로 정렬
- 정렬된 간선 중 순서대로 사이클을 형성하지 않는 간선 선택 (유니온 파인드)
- 해당 간선을 최소 신장 트리 집합(MST)에 추가
// 가중치가 있을 땐 클래스로 구현하는 방법이 좋음
class Edge {
int start;
int end;
int weight;
Edge(){}
Edge(int start, int end, int weight){
this.start = start;
this.end = end;
this.weight = weight;
}
}
// 간선들을 담을 클래스 배열 선언
Edge [] edges = new Edge[n];
// 정답을 기록할 answer 선언
int answer = 0;
for(Edge edge : edges){
// 간선들에 연결된 노드들의 루트가 다르다면!
if(find(edge.start) != find(edge.end)){
// 두 노드 연결
union(edge.start, edge.end);
// 가중치 더하기
ans += edge.weight;
}
}
