[백준] 2725번 보이는 점의 개수

https://www.acmicpc.net/problem/2725

import java.io.*;
 
public class Main {
   public static void main(String[] args) throws IOException {
      int[] count = new int[1001];
      count[1] = 3;
      int tmp;
      for(int i=2;i<1001;i++){
         tmp = 0;
         for(int j=1;j<i;j++){
            if(gcd(i,j)==1) tmp++;
         }
         count[i] = count[i-1] + tmp*2;
      }

      BufferedReader in = new BufferedReader(new InputStreamReader(System.in));
      int C = Integer.parseInt(in.readLine());
      StringBuilder sb = new StringBuilder();
      for(int i=0;i<C;i++){
         sb.append(count[Integer.parseInt(in.readLine())]).append('\n');
      }
      System.out.print(sb);
   }
   public static int gcd(int a, int b){
      if(b==0) return a;
      return gcd(b,a%b);
   }
}

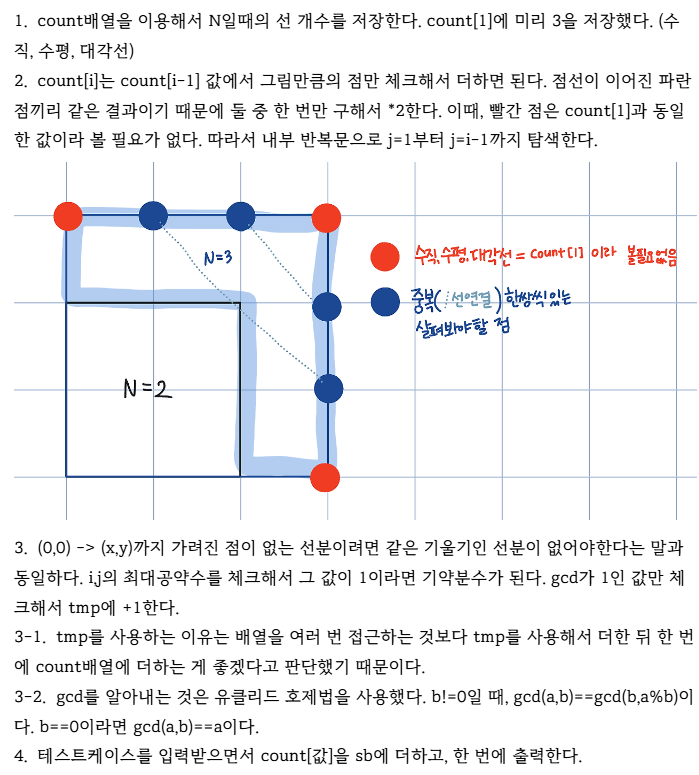
• 사전 계산 (Preprocessing):
  • count 배열을 이용해 N=1부터 N=1000까지의 각 N에 대한 보이는 점의 개수를 미리 계산합니다. N=1N = 1 N=1000N = 1000 NN
    
  • 초기값 count[1] = 3은 N=1일 때의 보이는 점을 나타냅니다. N=1N = 1
    
  • 각 N=2부터 1000까지, x=1부터 N−1까지의 y에 대해 gcd(x,y)=1인 경우를 세어 tmp에 저장하고, 이를 통해 count[i] = count[i-1] + tmp*2로 업데이트합니다. N=2N = 2 10001000 x=1x = 1 N−1N-1 yy gcd(x,y)=1gcd(x,y) = 1
    
• 테스트 케이스 처리:
  • 입력으로 주어진 테스트 케이스 수 C만큼 반복하여 각 테스트 케이스의 N에 대한 결과를 count[N]에서 조회하여 출력합니다. CC NN
    
• GCD 계산:
  • gcd 메서드를 통해 두 수의 최대 공약수를 재귀적으로 계산합니다.

• 목적: N=1N = 1N=1부터 N=1000N = 1000N=1000까지의 각 NNN에 대해 보이는 점의 개수를 미리 계산하여 count 배열에 저장합니다. 이를 통해 각 테스트 케이스에서 빠르게 결과를 조회할 수 있습니다.
• 초기 설정:
  • count[1] = 3: N=1일 때 보이는 점은 (1,0), (0,1), (1,1)로 총 3개입니다. N=1N = 1 (1,0)(1,0) (0,1)(0,1) (1,1)(1,1)
    
• 반복문:
  • 외부 루프: i=2부터 1000까지 반복합니다. 여기서 i는 현재 N을 나타냅니다. i=2i = 2 10001000 ii NN
    
  • 내부 루프: 각 i에 대해 j=1부터 i−1까지 반복하여 (i,j) 쌍의 gcd(i,j)를 계산합니다. ii j=1j = 1 i−1i-1 (i,j)(i,j) gcd(i,j)gcd(i,j)
    • gcd(i,j)=1gcd(i,j) = 1gcd(i,j)=1인 경우, 즉 i와 j가 서로소인 경우 tmp를 증가시킵니다. ii jj
      
  • 보이는 점 개수 업데이트:
    • count[i] = count[i-1] + tmp*2:
      • tmp: 현재 N=i일 때, x=i와 y=1부터 i−1까지 중 gcd(i,j)=1인 y의 개수입니다. N=iN = i x=ix = i y=1y = 1 i−1i-1 gcd(i,j)=1gcd(i,j) = 1 yy
        
      • tmp*2: (i,j)와 (j,i)는 서로 다른 점이므로 두 점을 모두 세기 위해 2를 곱합니다. (i,j)(i,j) (j,i)(j,i)
        
      • count[i-1]: 이전 N=i−1까지의 보이는 점 개수를 가져와서 현재 N=i일 때의 보이는 점 개수를 누적합니다. N=i−1N = i-1 N=iN = i

풀이 방법

1. 서로소 쌍의 개수 계산:
   • (x,y)(x,y)(x,y)가 보이려면 gcd(x,y)=1이어야 합니다. gcd(x,y)=1gcd(x,y) = 1
     
   • (x,y)(x,y)(x,y)와 (y,x)는 서로 다른 점이므로, 각 서로소 쌍을 두 번 세어야 합니다. (y,x)(y,x)
     
   • (x,0)(x,0)(x,0)과 (0,x)도 보이는 점이 됩니다. 예를 들어, x>0일 때 (x,0)과 (0,x)는 모두 보입니다. (0,x)(0,x) x>0x > 0 (x,0)(x,0) (0,x)(0,x)
     
2. 사전 계산을 통한 효율성 향상:
   • NNN의 최대값이 1000이므로, N=1부터 N=1000까지의 보이는 점의 개수를 미리 계산하여 count 배열에 저장합니다. N=1N = 1 N=1000N = 1000
     
   • 이를 통해 각 테스트 케이스에서 즉시 count[N]을 조회하여 결과를 얻을 수 있습니다.
3. 누적 합을 이용한 보이는 점의 개수 계산:
   • N=iN = iN=i일 때, 이전 N=i−1까지의 보이는 점 개수에 N=i일 때 추가되는 보이는 점을 더합니다. N=i−1N = i-1 N=iN = i
     
   • 추가되는 보이는 점은 (i,j)와 (j,i) 중 gcd(i,j)=1인 j의 개수에 2를 곱한 값입니다. (i,j)(i,j) (j,i)(j,i) gcd(i,j)=1gcd(i,j) = 1

시간 복잡도 분석

사전 계산 부분

• 외부 루프: i=2i = 2i=2부터 100010001000까지 반복 → O(N)O(N)O(N), 여기서 N=1000N = 1000N=1000
• 내부 루프: 각 iii에 대해 j=1j = 1j=1부터 i−1i-1i−1까지 반복 → O(i)O(i)O(i) 시간
• GCD 계산: 각 jjj에 대해 gcd(i,j)gcd(i,j)gcd(i,j)를 계산 → O(log⁡min⁡(i,j))O(\log \min(i,j))O(logmin(i,j)) 시간 (유클리드 호제법 기준)
• 총 시간 복잡도:

  • 외부 루프: O(N)

    O(N)O(N)
    

  • 내부 루프: ∑i=2NO(ilogi) → O(N2logN)

    ∑i=2NO(ilog⁡i)\sum_{i=2}^{N} O(i \log i)
    
    O(N2log⁡N)O(N^2 \log N)

    따라서, 사전 계산 부분의 총 시간 복잡도는 O(N2log⁡N)O(N^2 \log N)O(N2logN)입니다. 여기서 N=1000N = 1000N=1000이므로, 총 106×log⁡1000≈106×10=10710^6 \times \log 1000 \approx 10^6 \times 10 = 10^7106×log1000≈106×10=107 정도의 연산이 필요합니다. 이는 제한 시간 내에 충분히 수행 가능합니다.

전체 시간 복잡도

• 사전 계산: O(N2logN), N=1000 O(N2log⁡N)O(N^2 \log N) N=1000N = 1000
  
• 테스트 케이스 처리: O(C), C=1000 O(C)O(C) C=1000C = 1000
  
• 총 합: O(N2logN), O(107), 충분히 효율적입니다. O(N2log⁡N)O(N^2 \log N) O(107)O(10^7)

알고리즘 및 자료구조

알고리즘

1. 유클리드 호제법을 이용한 GCD 계산:
   • 두 정수 a와 b의 최대 공약수 gcd(a,b)를 재귀적으로 계산합니다. aa bb gcd(a,b)gcd(a,b)
     
   • 효율적인 GCD 계산을 통해 서로소 여부를 빠르게 판단합니다.
2. 서로소 쌍의 개수 누적 계산:
   • 각 N=i에 대해 x=i와 y=1부터 i−1까지의 y에 대해 gcd(i,y)=1인 경우를 세어 tmp에 저장합니다. N=iN = i x=ix = i y=1y = 1 i−1i-1 yy gcd(i,y)=1gcd(i,y) = 1
     
   • 이를 통해 (i,y)와 (y,i) 두 점을 동시에 세므로 tmp*2를 count[i]에 더합니다. (i,y)(i,y) (y,i)(y,i)
     
   • N=iN = iN=i일 때 보이는 점의 개수는 이전 N=i−1까지의 보이는 점 개수에 현재 N=i에서 추가되는 보이는 점을 더한 값입니다. N=i−1N = i-1 N=iN = i
     

자료구조

1. 배열 (count[1001]):
   • N=0N = 0N=0부터 N=1000까지의 보이는 점 개수를 저장합니다. N=1000N = 1000
     
   • 미리 계산된 값을 저장하여 테스트 케이스 처리 시 빠르게 조회할 수 있습니다.
2. 재귀 함수 (gcd):
   • 두 수의 GCD를 계산하기 위해 재귀적으로 호출됩니다.
   • 유클리드 호제법을 구현한 재귀 함수입니다.
3. 입출력 도구 (BufferedReader, StringBuilder):
   • BufferedReader: 빠른 입력을 위해 사용됩니다.
   • StringBuilder: 여러 개의 출력 결과를 효율적으로 저장하고 한 번에 출력하기 위해 사용됩니다. 이는 각 테스트 케이스마다 System.out.println을 호출하는 것보다 훨씬 빠릅니다.

참고
https://january-diary.tistory.com/entry/BOJ-2725-%EB%B3%B4%EC%9D%B4%EB%8A%94-%EC%A0%90%EC%9D%98-%EA%B0%9C%EC%88%98-JAVA