[Java] Random의 nextInt()에 대한 고찰

[문제 제기]

java.util.Random 에서 nextInt(2) 는 0 또는 1을 반환한다.
이 때, nextInt(2)의 값을 현재 시간과 연관하여 예측이 가능할까?

[seed]

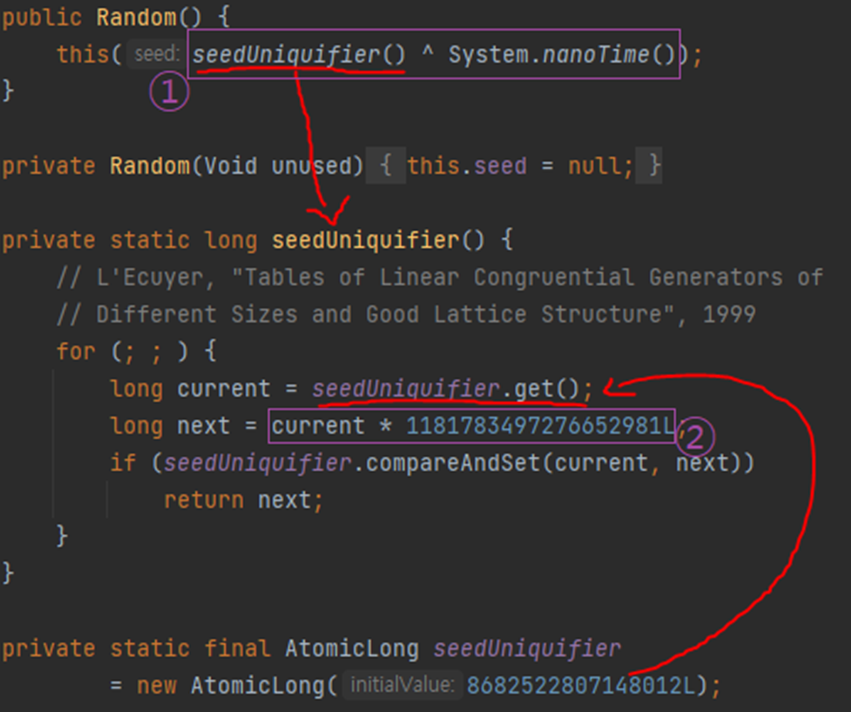
Random 의 생성자에 seed값을 인자로 넘겨주기도 하지만 일반적으로 난수를 기대하기 때문에 seed를 설정하지 않는다.

위 사진의 ①을 보면 생성자에 인자가 없을 경우 seedUniquifier() ^ System.nanoTime() 을 seed로 설정함을 알 수 있다.
seedUniquifier()은 ②에서 볼 수 있듯 곱셈을 통해 seedUniquifier값이 계속 변경된다.
즉, new Random() 을 수행할 때마다 seedUniquifier의 값이 변경된다.

아무리 단순화하여 new Random()을 최초 1회 수행한다고 하더라도 XOR 연산부터 예측 가능성이 떨어진다.

seed를 넘겨줬다고 해보자. 그 다음엔 어떤 일이 일어날까.

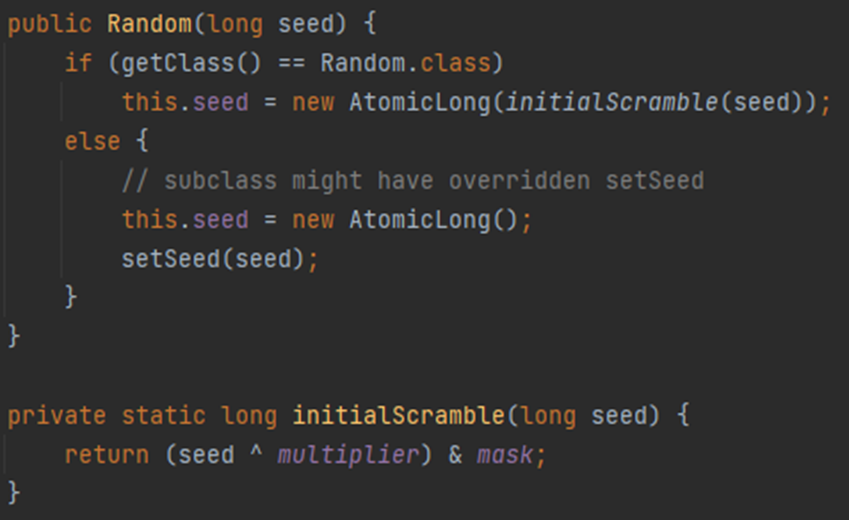
즉 객체의 seed는 (seed ^ multiplier) & mask와 같다.
각 상수를 10진수로 표현하면 다음과 같다.

multiplier = 25214903917
addend = 11
mask = 2^48 – 1

mask와 AND 연산을 하면 하위 48비트만 취한다는 것으로 Random 객체의 seed의 값은 48비트로 표현할 수 있는 수가 된다.

[next()]

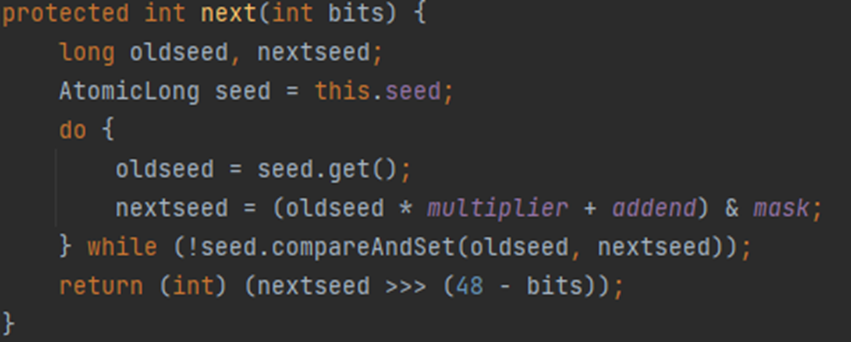
nextInt()를 보기 전에 next(31)의 반환값을 알아야한다.

현재 seed를 oldseed로 하여 수식을 통해 nextseed를 만들고, seed에 nextseed 값을 복사한다.
nextseed의 수식은 선형 합동 생성기로 유사 난수 생성기이다.
역시 mask와 AND 연산을 통해 하위 48비트만 취한다는 것을 알 수 있다.
반환값은 nextseed의 상위 bits비트만 취한 int형임을 알 수 있다.
즉, next(31)의 반환값은 31비트로 표현 가능한 정수이다.

[nextInt()]

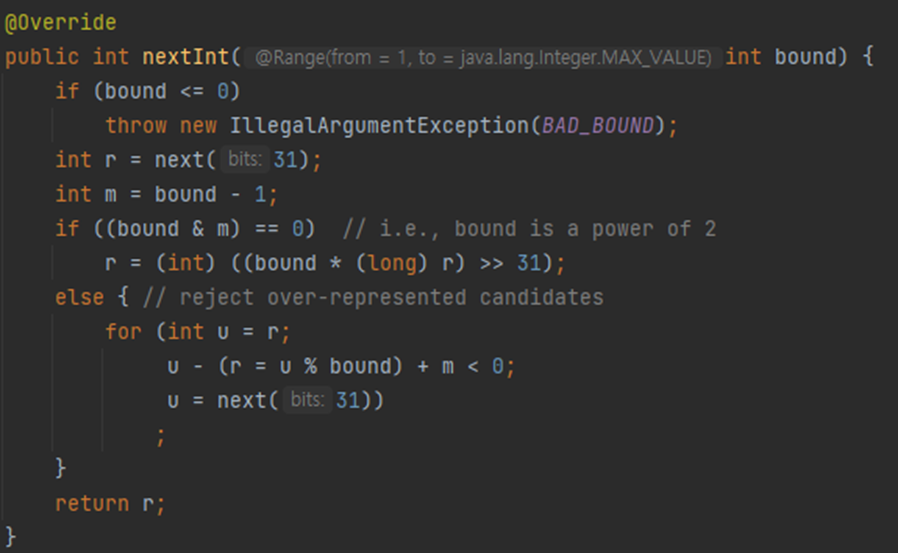
편의상 bound가 2의 거듭제곱이라고 해보자. 즉 bound = 2^n 이다.
그렇다면 nextInt(bound)의 값은 (int) (bound * (long) next(31) >> 31) 이다.
bound * (long) next(31) 은 bound가 2^n 이므로 (31+n)비트 수임을 알 수 있다.
즉, nextInt(bound)의 반환값은 n비트 수이다.
따라서 bound = 2^n 일 때 nextInt(bound)는 0 ~ 2^n-1 이 반환된다.

nextInt(2) 에 주목해보자.
nextInt(2) 가 1이라면 next(31)의 최상위비트는 1이고, 0일 때는 0이다.
next(31)의 값은 nextseed에 따라 결정되고, nextseed가 2^47보다 크거나 같다면 1, 아니면 0인 것이다.

[결론]

사람이 직관적으로 시간과 연관지어 nextseed의 값을 예측하기란 쉽지 않다.
따라서, nextInt(2)의 값을 예측하기란 쉽지 않다. 그냥 50%로 찍는게 편하다.