백준 KCM Travel(10217)

KCM Travel

1. 힌트

1) 단순 다익스트라에서 비용이 $M$을 넘지 않는 경로로만 이동하는 최단 경로는 정답이 아닙니다. 반례는 다음과 같습니다.

1
4 4 4
1 2 1 1
2 3 1 1
3 4 1 1
1 3 3 1
->2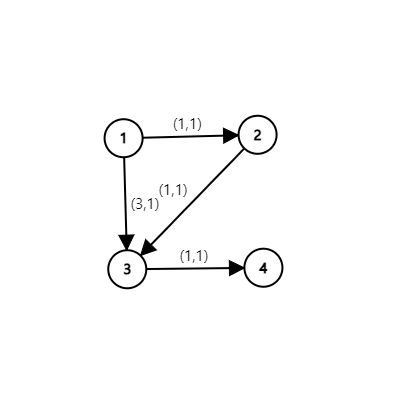

2) $N$이 최대 $100$으로 상당히 작은 것에 주목합니다. 그래프를 변형해서 모델링해볼 수 있습니다.

3) 정점을 2차원으로 늘려서 생각합니다. ($i$번 정점, $x$만큼 비용을 사용함)으로 정의하면 전체 정점의 개수는 $10^6$이므로 이 정도면 오래걸리긴 하겠지만 $ElgV$의 다익스트라로 해결할 수 있습니다.

2. 접근

1) 비슷한 문제를 풀어본 적이 있던가?

다익스트라로 한 정점에서 나머지 모든 정점으로의 최단 거리를 구할 수 있습니다. 여기서 거리는 소요 시간이므로 가장 짧은 시간이 소요되는 경로부터 확인해보면 되는데, $M$이하로 비용을 사용해야 하는 것이 발목을 잡습니다. 대개 이런 경우 그래프를 색다르게 모델링하면 풀 수 있습니다. 특히 이 문제에서는 $N$이 $100$이하인 것이 눈에 띕니다.
따라서 정점을 2차원으로 늘려서 생각합니다. ($i$번 정점, $x$만큼 비용을 사용함)으로 생각하고 $N$번째 정점에 비용을 얼만큼 사용했건 다익스트라로 가장 짧은 소요 시간을 찾습니다.

3. 구현

public class Main {
	static int N, M;
	static ArrayList<ArrayList<Tuple>> adj;
	
	static final int INF = 987654321;
	
	static int dijkstra() {
		PriorityQueue<Tuple> pq = new PriorityQueue<>();
		pq.offer(new Tuple(1, 0, 0));
		// N번 정점까지 M비용을 소모했을 때 최단 거리
		int[][] time = new int[N + 1][M + 1];
		for (int i = 0; i <= N; i++) Arrays.fill(time[i], INF);
		time[1][0] = 0;
		while (!pq.isEmpty()) {
			Tuple t = pq.poll();
			int here = t.num;
			int hereCost = t.cost;
			int hereTime = t.time;
			if (time[here][hereCost] < hereTime) continue;
			for (Tuple e : adj.get(here)) {
				int there = e.num;
				int thereCost = hereCost + e.cost;
				int thereTime = hereTime + e.time;
				if (thereCost <= M && time[there][thereCost] > thereTime) {
					time[there][thereCost] = thereTime;
					pq.offer(new Tuple(there, thereCost, thereTime));
				}
			}
		}
		int min = time[N][0];
		for (int i = 1; i <= M; i++) min = Math.min(min, time[N][i]);
		return min;
	}
	
	public static void main(String[] args) throws IOException {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		StringBuilder bw = new StringBuilder();
		int TC = Integer.parseInt(br.readLine());
		while (TC-- > 0) {
			StringTokenizer st = new StringTokenizer(br.readLine(), " ");
			N = Integer.parseInt(st.nextToken());
			M = Integer.parseInt(st.nextToken());
			int K = Integer.parseInt(st.nextToken());
			adj = new ArrayList<>(N);
			for (int i = 0; i <= N; i++) adj.add(new ArrayList<>());
			for (int i = 0; i < K; i++) {
				st = new StringTokenizer(br.readLine(), " ");
				int u = Integer.parseInt(st.nextToken());
				int v = Integer.parseInt(st.nextToken());
				int c = Integer.parseInt(st.nextToken());
				int d = Integer.parseInt(st.nextToken());
				adj.get(u).add(new Tuple(v, c, d));
			}
			int ret = dijkstra();
			bw.append(ret == INF ? "Poor KCM" : ret).append("\n");
		}
		System.out.print(bw);
	}

}

class Tuple implements Comparable<Tuple> {
	int num, cost, time;
	
	Tuple(int n, int c, int t) { num = n; cost = c; time = t;}
	
	public int compareTo(Tuple o) { return time - o.time; }
	
}

1) 시간 복잡도

2) 테스트 케이스