백준 체스판(12960)

체스판

1. 순서를 강제할 수 있을까?

우리가 찾고자 하는 해는 체스판에 L-모양의 타일이 조건을 만족하게 놓여있는 상태중에서 가장 타일이 많이 올려져있는 상태이다. 그렇다면 조건을 만족해서 타일을 배치하는 방법을 모두 시도해보고 그중에서 최적해를 찾는 것이 가장 직관적이다. 경우의 수를 모두 계산하기 위해서는 재귀 호출의 각 단계에서 고르는 각 선택지에 다음과 같은 속성이 성립해야 한다. (출처 : 종만북)
a) 모든 경우는 이 선택지에 포함됨
b) 어떤 경우도 두 개 이상의 선택지에 포함되지 않음

타일을 놓는 순서는 문제의 답과 상관이 없다. 따라서 우리는 순서를 강제해서 체스판의 왼쪽 위부터 L-모양 타일을 놓는것을 시도해보자. 체스판의 어떤 지점 $(i, j)$에서 가능한 선택은 다음과 같다.
1. 타일을 놓지 않는다. (놓을 수 있더라도)
2. 타일을 놓는다 (놓을 수 있는 경우)
타일을 회전시켜서 놓는 방법은 다양하지만 타일의 모양은 4가지 뿐이다.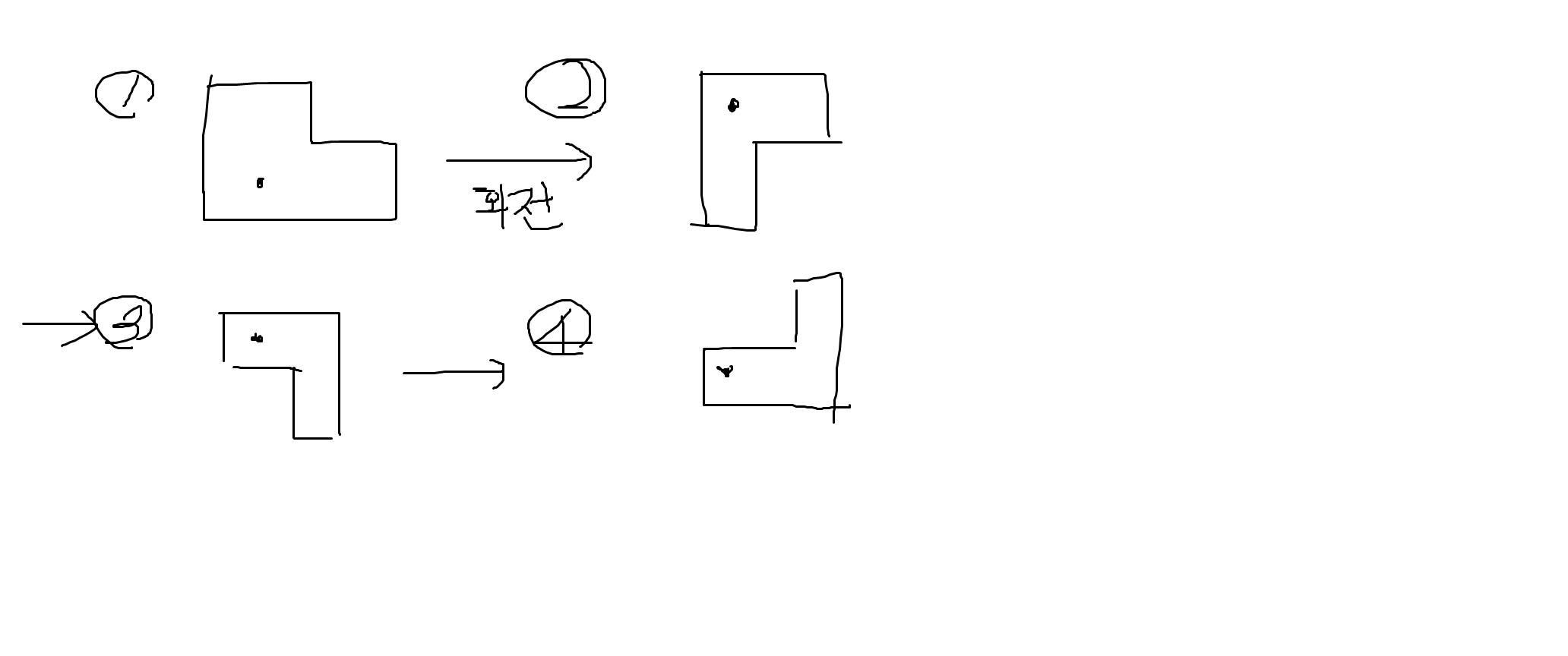
모든 타일의 종류는 이 4가지 중에 속하고, 어떤 경우도 두 개 이상 종류에 속하지 않는다. 점은 $(i, j)$의 위치.

2. 이전 선택에 관련된 정보

그런데 1번 선택은 언제나 가능한 반면에 2번선택은 경우에 따라서는 불가능할 때가 있다. 체스판의 범위를 벗어나거나, 이전에 놓은 타일과 겹칠 수도 있기 때문이다.
타일의 가로 길이는 길어봐야 2칸이므로 바로 이전 열 $(j - 1)$에서 타일을 놓은 정보만 알고 있으면 된다.

3. 시간 복잡도

아주 간단하게 생각하면 $R \times C$ 넓이의 체스판의 $(i, j)$마다 5가지 선택이 가능하므로 시간 복잡도는 $O(5^{R \times C})$이 되어버린다.

우리는 여기서 $j$번째 열에 타일이 배치되어있는지 여부가저장된 $R$크기의 비트필드만 주어졌으면 언제나 답이 같음을 알 수 있다. $1 ≤ R ≤ 4$이기 때문에 크기도 적절하다. 이처럼 참조적 투명성을 만족하기 때문에 DP함수를 작성할 수 있고, 존재하는 부분 문제의 수는 $O(C \times 2^R)$이 되고, DP함수 하나의 시간 복잡도는 $O(2^R)$이므로 최종 시간 복잡도는 $O(C \times 2^{2R})$이 된다.

4. 구현

1. dp(int j, int b)

부분 문제들을 $[j, C)$로 나누었다. $R$이 더 작기 때문에 이 문제에서는 왼쪽에서 오른쪽으로 진행한다.

3. btk(int j, int i, int b, int nb)

dp함수 내에서 모든 경우를 시도하게 구현하기가 복잡해서 따로 함수로 구현해주었다. 모든 경우를 시도하고 맨 마지막에는 다음 dp함수를 호출하여서 답을 구한다.

public class Main {
	static int N, M; static boolean[][] S; // 이미 놓여져 있는지 여부
	static int[][] cache;
	
	// [j, M)의 체스판에 놓을 수 있는 타일의 최대 개수
	// j번째 열에 놓여져 있는지 여부는 b에 비트마스킹으로 나타냄
	static int dp(int j, int b) {
		if (j == M - 1) return 0; // 타일은 오른쪽으로 튀어나와 있으므로 맨 마지막 칸에 설치 불가
		if (cache[j][b] != -1) return cache[j][b];
		return cache[j][b] = btk(j, 0, b, 0);
	}
	
	static int btk(int j, int i, int b, int nb) {
		if (i == N) return dp(j + 1, nb);
		// 현재 칸이나 오른쪽 칸이 이미 놓여져있는 경우 놓을 수 없다.
		if (S[i][j] || S[i][j + 1] || (b & (1 << i)) > 0 || (nb & (1 << i)) > 0)
			return btk(j, i + 1, b, nb);
		int max = btk(j, i + 1, b, nb); // 놓지 않는 경우
		b |= (1 << i); nb |= (1 << i);
		// ㄴ모양 : 현재 칸이 검정 칸이고, 위쪽 타일이 놓을 수 있어야 함
		if ((i + j) % 2 == 0 && i - 1 >= 0 && !S[i - 1][j] && (b & (1 << (i - 1))) == 0)
			max = Math.max(max, 1 + btk(j, i + 1, b, nb));
		// 90도 회전 : 현재 칸이 검정 칸이고, 아래쪽 타일이 놓을 수 있어야 함
		if ((i + j) % 2 == 0 && i + 1 < N && !S[i + 1][j] && (b & (1 << (i + 1))) == 0)
			max = Math.max(max, 1 + btk(j, i + 2, b | (1 << (i + 1)), nb));
		// 90도 회전 : 현재 칸이 흰색 칸이고, 오른쪽 아래 타일이 놓을 수 있어야 함
		if ((i + j) % 2 == 1 && i + 1 < N && !S[i + 1][j + 1])
			max = Math.max(max, 1 + btk(j, i + 1, b, nb | (1 << (i + 1))));
		// 90도 회전 : 현재 칸이 흰색 칸이고, 오른쪽 위 타일이 놓을 수 있어야 함
		if ((i + j) % 2 == 1 && i - 1 >= 0 && !S[i - 1][j + 1] && (nb & (1 << (i - 1))) == 0)
			max = Math.max(max, 1 + btk(j, i + 1, b, nb | (1 << (i - 1))));
		return max;
	}
	
	public static void main(String[] args) throws IOException {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		StringTokenizer st = new StringTokenizer(br.readLine(), " ");
		N = Integer.parseInt(st.nextToken());
		M = Integer.parseInt(st.nextToken());
		S = new boolean[N][M];
		for (int i = 0; i < N; i++) {
			String row = br.readLine();
			for (int j = 0; j < M; j++) S[i][j] = row.charAt(j) == 'X';
		}
		cache = new int[M][1 << N];
		for (int i = 0; i < M; i++) Arrays.fill(cache[i], -1);
		System.out.println(dp(0, 0));
	}
	
}