백준 Project Teams(20044)

axiom·2021년 10월 11일

Project Teams

1. 힌트

1) 수열을 원소를 두 개씩 짝지어서 팀을 구성합니다. 이 때 가장 코딩 역량이 작은 팀이 최대화되도록 해야합니다.

2) 주어진 수열을 오름차순으로 정렬해봅니다.

3) 양 끝부터 두 개씩 짝지어서 팀을 구성하는 것이 최적해입니다. 그러한 과정에서 코딩 역량의 합이 가장 작은 팀이 문제의 정답이 됩니다.

2. 접근

1) 주어진 수열을 정렬하기

우리가 하는 일은 두 명씩 짝지어서 팀을 구성하는 것이므로 수열의 순서를 바꿔도 상관이 없습니다. 주어진 수열을 오름차순으로 정렬해봅시다.

2) 순서를 고정하고 최적해 찾기

$n \le 5000$ 이므로 당연히 완전 탐색으로는 불가능합니다. 그렇다는 것은 그리디한 해법이 존재하는 걸까요? 학생을 짝짓는 순서는 상관이 없으므로 코딩 역량이 작은 학생부터 그 학생에게 맞는 최적의 학생을 짝짓도록 순서를 강제해봅시다.

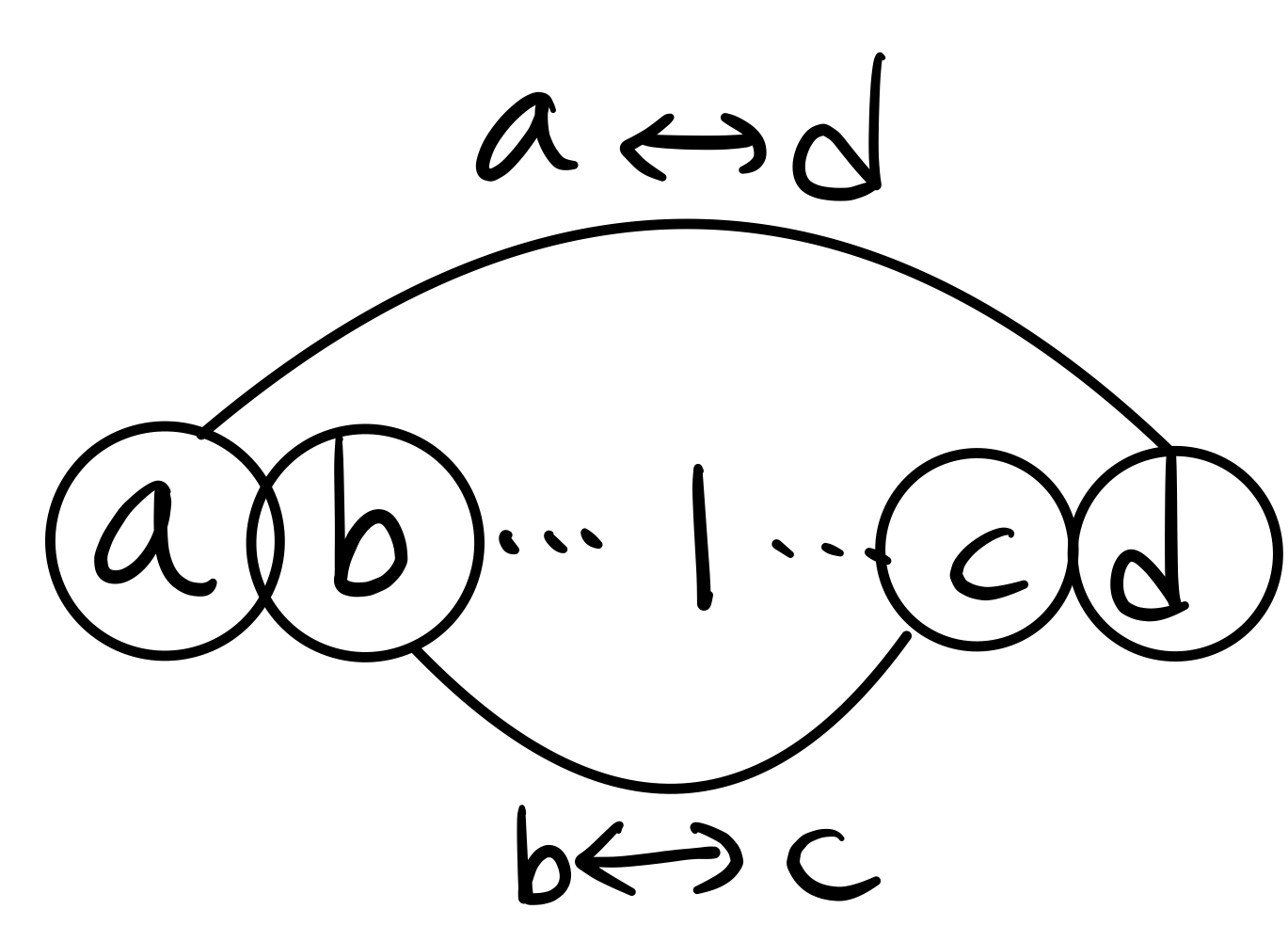
이와 같이 정렬해서 코딩 역량이 $a,\ b,\ ... \ c,\ d$ 인 수열을 생각해봅시다. 코딩 역량이 $a$ 인 학생을 짝지어 줄 때, 맨 오른쪽 끝에 있는 $d$ 와 짝지어주고, 마찬가지로 그 다음 $b$ 도 $c$ 와 짝지어주는 것이 최적의 방법입니다. 문제의 정답은 이렇게 해서 만든 $n$ 개의 팀중에서 가장 작은 코딩 역량을 가진 팀이 됩니다. 어떻게 증명할 수 있을까요?

3) 증명

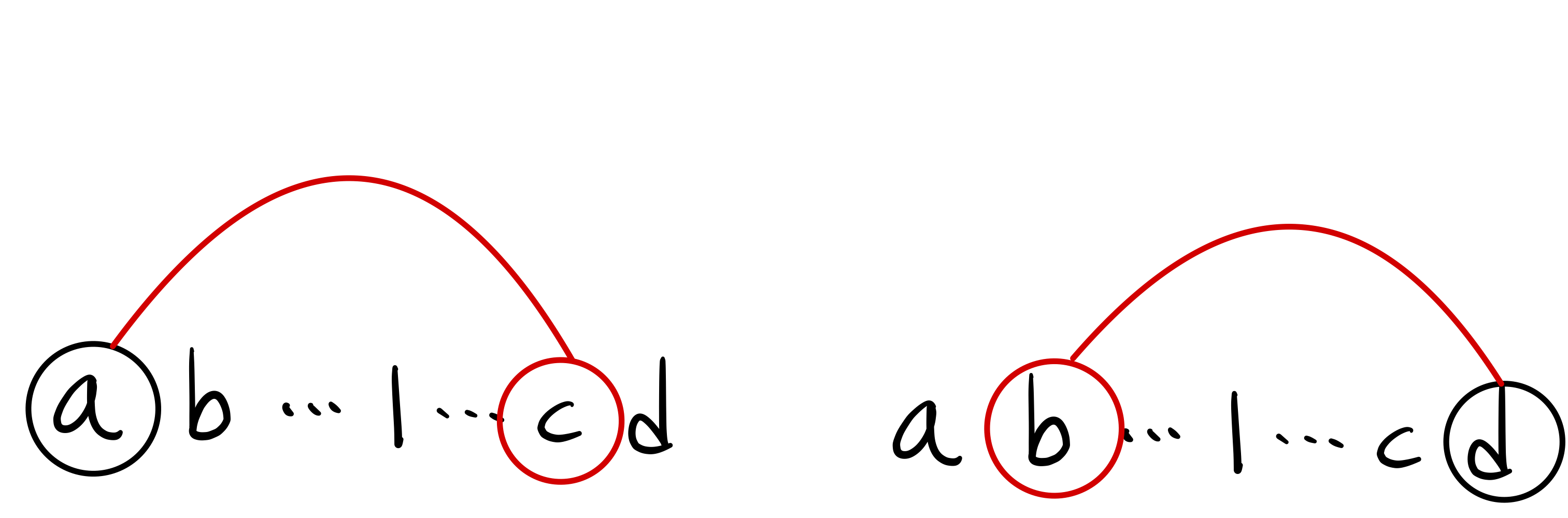
어째서 이렇게 짝짓는 것이 최적해일까요? 귀류법으로 이를 증명해보겠습니다. 귀류법을 통한 증명은, 우리가 가정한 방법을 따르지 않고 최적해를 만드는 방법이 있다고 가정하고, 사실은 그것이 불가능함을 증명해서 우리가 가정한 방법이 언제나 최적해를 찾는다는 것을 증명하는 것입니다. 위 그림은 $(a,d),\ (b,c)$ 대신에 $(a,c),\ (b,d)$ 를 짝지은 상황입니다. 나머지 안쪽은 우리가 가정한 방법과 똑같이 짝지어줬다고 가정합시다. 그런데 이렇게 짝지어서 마찬가지로 최적해가 나왔다는 것은 모순입니다. 나머지 부분은 똑같이 짝지었으므로 $a,b,c,d$ 만 생각해서

$(a,d)$ 가 최소였다면, 이 대신 $(a,c)$ 를 짝지은 방법은 $(a,d)$ 보다 더 작아지므로 모순입니다.
$(b,c)$ 가 최소였다면, 이 대신 $(a,c)$ 를 짝지은 방법은 $(b,c)$ 보다 더 작아지므로 모순입니다.
이 학생들의 코딩 역량이 모두 서로 다르므로 가능한 증명입니다.
따라서 우리가 가정한 방법이 언제나 최적해를 찾습니다.

3. 구현

public class Main {

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        int N = Integer.parseInt(br.readLine());
        StringTokenizer st = new StringTokenizer(br.readLine(), " ");
        ArrayList<Integer> S = new ArrayList<>();
        for (int i = 0; i < 2 * N; i++) S.add(Integer.parseInt(st.nextToken()));
        Collections.sort(S);
        int head = 0; int tail = 2 * N - 1;
        int min = Integer.MAX_VALUE;
        while (head < tail) {
            min = Math.min(min, S.get(head) + S.get(tail));
            head++; tail--;
        }
        System.out.println(min);
    }

}