백준 빵 정렬(5000)

빵 정렬

1. 힌트

1) 현재 주어진 수열을 $S_1$이라 하고 만들어야 하는 수열을 $S_2$라고 하겠습니다. 임의의 연속하는 세 원소를 제외하고는 언제나 원하는 순서로 맞출 수 있습니다.

2) 빵 정렬의 연산 특성 상, 전체 수열의 Inversion의 기우성(홀짝성)이 유지됨을 알 수 있습니다. 따라서 $S_1$과 $S_2$가 기우성이 다르다면 절대로 똑같이 맞춰줄 수 없습니다.

3) 기우성이 같다면 언제나 똑같이 만들 수 있을까요? $S_1$에서 세 원소를 빼고 $S_2$와 맞게 정렬해줍니다. 서로 맞춰진 부분은 제외하고, 나머지 부분을 각각 $X_1, X_2$라고 하겠습니다. 빵 정렬 연산이 계속 순환한다는 점을 확인하면 $X_1$에만 정렬 연산을 하면 반드시 $X_2$를 만들어낼 수 있음을 알 수 있습니다.

2. 접근

1) 빵 정렬 연산의 특성 파악하기

이런 특이한 연산이 주어지면 가장 좋은 접근 방법은 직접 손으로 해보면서 연산의 특성을 파악하는 것입니다. 피연산자가 될 세 원소를 $a, b, c$라고 하면 다음과 같은 연산의 특성을 파악할 수 있습니다.

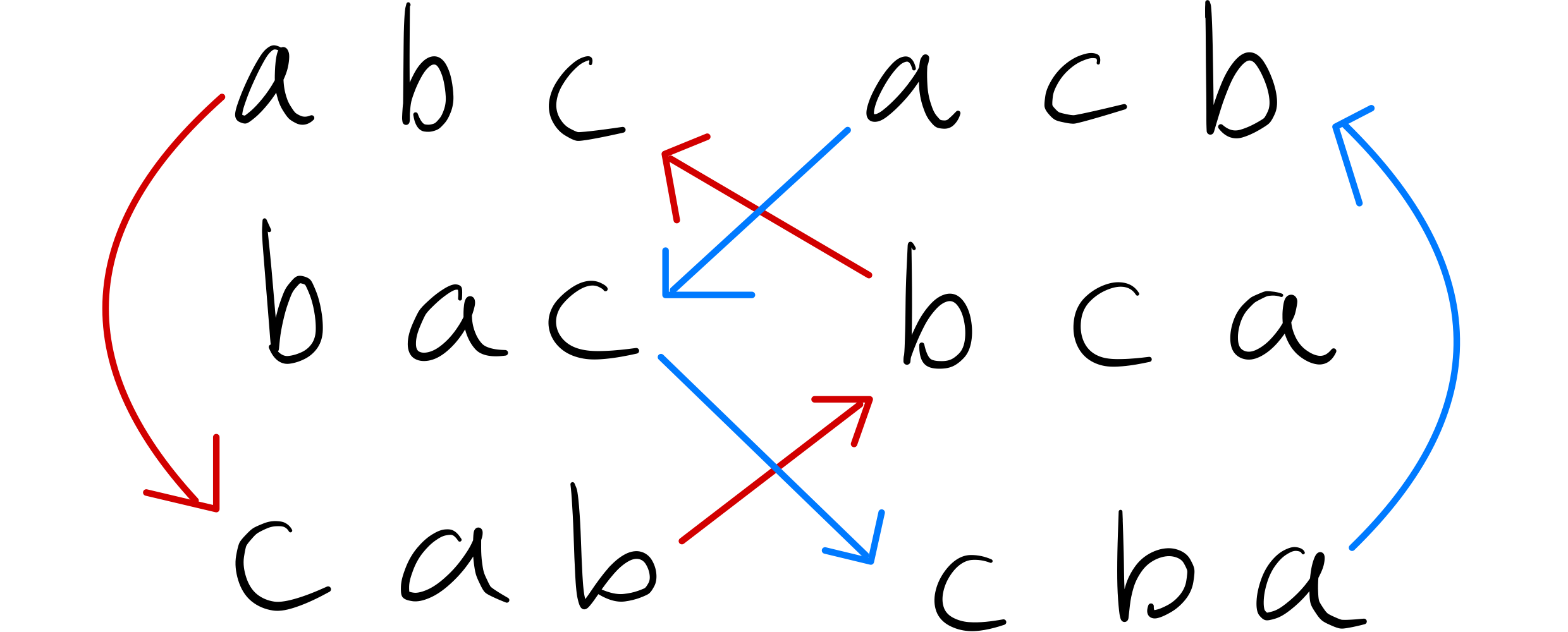
연산을 아무리 해도 $abc,\ cab,\ bca$가 $acb,\ bac,\ cba$가 되는 것은 불가능합니다.

2) 수열의 기우성(홀짝성)

위의 연산에서 $a < b < c$라고 가정하면 Inversion의 기우성이 유지됨을 알 수 있습니다. 빵 정렬 연산으로 전체 수열의 Inversion의 수는 $+2, -2, +0$만큼 변하기 때문이죠.
Inversion : ($S[i] > S[j], (i < j)$를 만족하는 순서쌍 $(i, j)$의 개수)

빵의 현재 순서를 $S_1$이라고 하고 사장이 원하는 순서를 $S_2$라고 합시다. 또, $f(S) =$ 수열 $S$의 Inversion이 짝수면 $0$ 홀수면 $1$을 반환하는 함수라고 정의합시다.
$f(S_1) \neq f(S_2)$라면 죽었다 깨어나도 $S_1$을 $S_2$로 만드는 것은 불가능하다는 것은 당연히 알 수 있습니다.
그렇다면 $f(S_1) = f(S_2)$라면 언제나 $S_1$을 $S_2$로 만드는 것이 가능할까요? 가능합니다. 그 과정은 다음과 같습니다.

3) 연속하는 세 원소만 빼고 같게 만들기

수열 $S_1$에서 적절한 연산을 통해서 어떤 임의의 연속하는 세 원소만 빼고 나머지는 $S_2$랑 똑같게 만들어줄 수 있습니다.

만약 위 그림처럼 $S_1$에서 $a,\ b,\ c,\ d$ 네 개 이상의 원소가 $S_2$와 맞춰지지 않았고, 나머지 부분은 똑같이 맞춰졌다고 가정합시다. $S_1$에 있는 $d$를 $S_2$에 있는 $d$의 위치로 보내야합니다. 이럴 때, 언제나 $d$를 제자리로 보내줄 수 있습니다.

이런식으로 $x$를 $2$칸씩 옮기면 수열의 나머지 부분($a,\ b$)의 순서에는 영향을 끼치지 않으면서 옮길 수 있기 때문입니다. 현재 $d$의 위치와, $d$가 옮겨져야하는 위치가 짝수칸만큼 차이가 나면 이와 같은 방법으로 옮길 수 있습니다. 홀수칸만큼 차이가 난다면 $b,\ c,\ d$에 빵 정렬 연산을 두 번 해서 $c,\ d,\ b$로 만들어주면 됩니다. 이러면 다시 짝수칸만큼 차이가 나게 되죠. 우리는 최소 횟수를 구하는 것이 아니기 때문에 이렇게 해줘도 됩니다. 또 $d$를 제외한 세 원소 $a,\ b,\ c$는 어차피 $S_2$랑 맞출 마음이 없었으니 막 섞어버려도 됩니다.

4) 맞추지 못한 원소들의 기우성(홀짝성)

$f(S_1) = f(S_2)$라면 언제나 같게 만들 수 있음을 계속 증명해보겠습니다. 3절에서 세 원소를 제외한 나머지는 언제나 같게 만들 수 있음을 증명했으니 편의상 그 연속하는 세 원소를 맨 왼쪽에 있는 세 원소라고 합시다.
그 세 원소를 $X_1, X_2$라고 하면 $S_1 = X_1 + {X_1}^c, S_2 = X_2 + {X_2}^c$로 나타낼 수 있습니다.

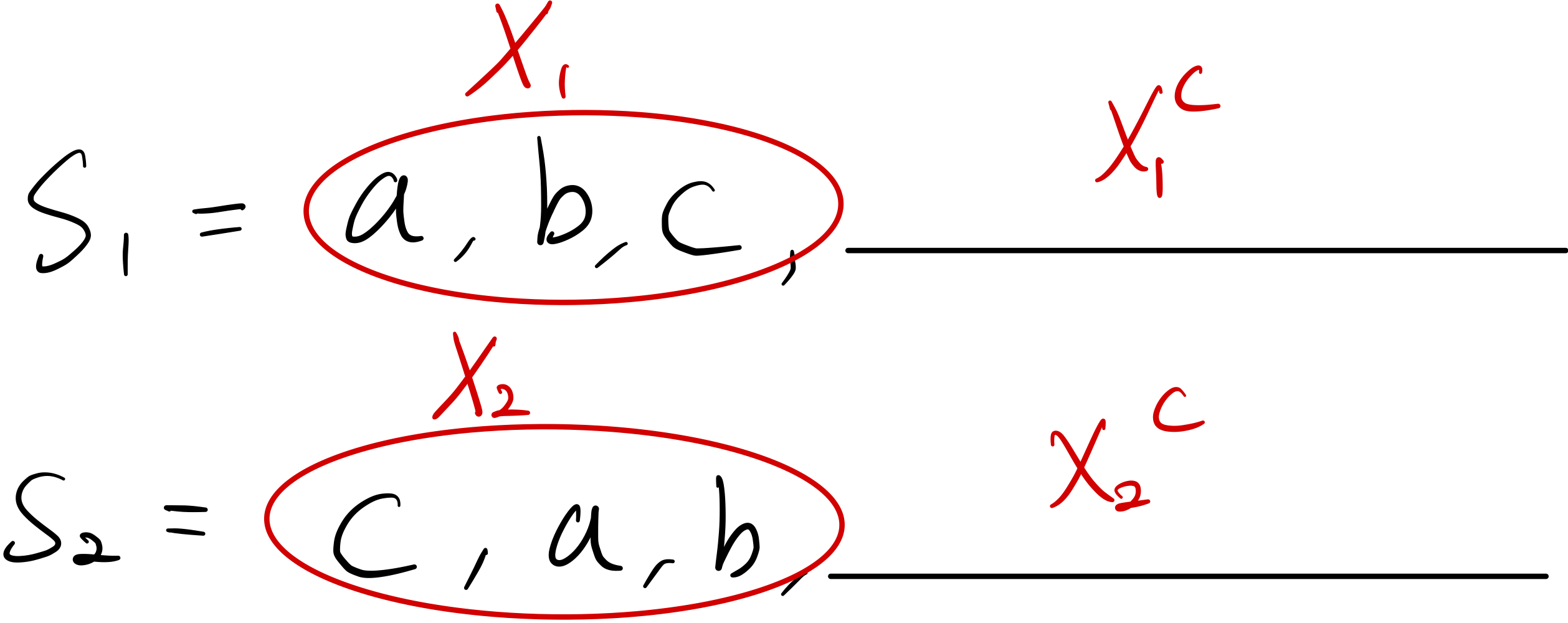
${X_1}^c = {X_2}^c$이기 때문에(같게 만들어준다고 했으므로) 각각의 수열에서 $X_1,\ X_2$만 생각해봅시다. $f(S_1) = f(S_2)$라면 $f(X_1) = f(X_2)$임을 알 수 있습니다. 1절에서 그림을 확인하면 기우성이 같은 $a,\ b,\ c$의 순열끼리는 언제나 바꿔줄 수 있음을 확인할 수 있습니다.
따라서 $f(S_1) = f(S_2)$라면 언제나 같게 만들 수 있습니다.

3. 구현

수열의 Inversion을 세는 방법은 빈 수열에서 시작해서 세그먼트 트리를 사용해서 가장 큰 원소부터 넣으면서 자신보다 왼쪽에 원소가 있다면 그 원소들의 개수만큼(서로 같은 원소는 없으므로) Inversion을 추가해주는 식으로 구현할 수 있습니다.

public class Main {

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        int N = Integer.parseInt(br.readLine());
        int[] S1 = new int[N + 1];
        StringTokenizer st = new StringTokenizer(br.readLine(), " ");
        for (int i = 1; i <= N; i++) S1[i] = Integer.parseInt(st.nextToken());
        int[] P1 = new int[N + 1];
        for (int i = 1; i <= N; i++) P1[S1[i]] = i;
        FenwickTree t1 = new FenwickTree(N + 1);
        long sum1 = 0;
        // 큰 수 부터 수열을 만들어나가면서 Inversion을 센다.
        // 만약 지금 넣은 수 왼쪽에 원소가 있다면 그 원소들은 모두 Inversion이 된다.
        for (int i = N; i >= 1; i--) {
            sum1 += t1.sum(P1[i]);
            t1.add(P1[i], 1);
        }
        int[] S2 = new int[N + 1];
        st = new StringTokenizer(br.readLine(), " ");
        for (int i = 1; i <= N; i++) S2[i] = Integer.parseInt(st.nextToken());
        int[] P2 = new int[N + 1];
        for (int i = 1; i <= N; i++) P2[S2[i]] = i;
        FenwickTree t2 = new FenwickTree(N + 1);
        long sum2 = 0;
        // 큰 수 부터 수열을 만들어나가면서 Inversion을 센다.
        // 만약 지금 넣은 수 왼쪽에 원소가 있다면 그 원소들은 모두 Inversion이 된다.
        for (int i = N; i >= 1; i--) {
            sum2 += t2.sum(P2[i]);
            t2.add(P2[i], 1);
        }
        System.out.println(((sum1 % 2) ^ (sum2 % 2)) == 0 ? "Possible" : "Impossible");
    }

}
class FenwickTree {
    long[] tree;
    
    FenwickTree(int n) { tree = new long[n + 1]; }

    void add(int pos, int val) {
        while (pos < tree.length) {
            tree[pos] += val;
            pos += (pos & -pos);
        }
    }

    long sum(int pos) {
        long ret = 0;
        while (pos > 0) {
            ret += tree[pos];
            pos -= (pos & -pos);
        }
        return ret;
    }

}