백준 핑크 플로이드(6091)

핑크 플로이드

1. 힌트

1) 인접 행렬 $S$의 위에서 플로이드-워셜 알고리즘을 사용하면 모든 $S[i][j]$는 $(i,\ j)$의 최단 거리를 저장하게 됩니다.

2) 인접 행렬 $S$에서 $i$번째 행에서 $S[i][i]$를 제외한 최솟값 $S[i][x]$는 분명 원래의 트리에서 직접 이어져 있었을 것입니다. 이러면 간선 $(i,\ x)$는 알 수 있는데, $i$번 정점에 이어진 간선이 이것 외에도 더 많을 수도 있습니다.

3) 언제나 가장 작은 간선부터 고르면 그 간선은 실제 트리를 구성하던 간선입니다. 단, 트리 형태가 깨지면 안됩니다. 이는 최소 스패닝 트리를 구하는 방식과 동일합니다.

2. 접근

1) 단순한 방법에서 시작할 수 있을까?

플로이드-워셜을 적용해버려서 인접 행렬이 최단 거리를 나타내는 행렬이 되어버렸습니다. 이러면 직접 이어져있지 않더라도 $(i,\ j)$사이의 최단 거리가 쓰여 있습니다. 하지만 하나는 확실히 알 수 있습니다. 최단 거리 행렬에서 $i$번째 행을 쭉 보면서 가장 작은 것을 $S[i][x]$라고 하면 $(i,\ x)$는 원래 트리에서도 실제로 이어져있었습니다. 트리에서 직접 이어져 있는 간선은 최단 거리 행렬에서도 동일하게 가장 작기 때문입니다.

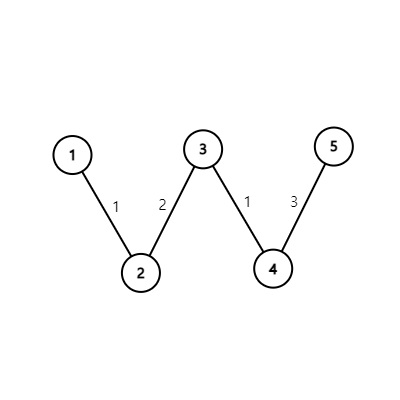
조금 이상하게 생겼지만 이러한 트리를 생각해봅시다. 최단 거리 행렬을 구하면 다음과 같습니다.

0 1 3 4 7 (어차피 양방향 간선이기 때문에 N-1개의 행이면 됩니다.)
  0 2 3 6
    0 1 4
      0 3
        0

$4$번째 정점을 잡고 행렬의 $4$번째 열을 살펴보면 당연히 가장 작은 $(4,\ 3)$간에 간선이 있다는 것은 알 수 있습니다. 그렇다면 $4$번째 열에서 두 번째로 작은 값은 가중치 $3$짜리 $(4,\ 2)$인데, 위 그래프를 보면 알 수 있지만 실제로 있는 간선이 아닙니다.
이러한 오류를 피하려면 전체 최단 거리 행렬에서 언제나 가장 작은 간선부터 선택해야 합니다. 간선의 가중치는 양수이기 때문에 위의 그림같은 경우에 가중치가 $w$인 간선을 고르기 전에 반드시 가중치가 $u,\ v$인 더 작은 간선을 먼저 고릅니다.
물론 그렇게 한 후에 가중치가 $w$인 간선은 고를 수 없습니다. 트리의 형태가 깨지기 때문입니다. 그런데, 가장 작은 간선 부터 고르고, 트리의 형태를 유지시키고, 어디서 많이 본 알고리즘입니다. 바로 최소 스패닝 트리를 구하는 크루스칼 알고리즘입니다. 이를 그대로 적용해주면 됩니다.

3. 구현

public class Main {
	
	public static void main(String[] args) throws IOException {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		StringBuilder bw = new StringBuilder();
		int N = Integer.parseInt(br.readLine());
		// N^2개의 간선을 저장
		ArrayList<Edge> S = new ArrayList<>(N * N);
		for (int u = 1; u <= N - 1; u++) {
			StringTokenizer st = new StringTokenizer(br.readLine(), " ");
			for (int v = u + 1; v <= N ; v++) {
				int w = Integer.parseInt(st.nextToken());
				S.add(new Edge(u, v, w));
			}
		}
		Collections.sort(S);
		// 원래 트리를 구성하는 간선들
		ArrayList<Edge> T = new ArrayList<>(N);
		DisjointSet s = new DisjointSet(N + 1);
		for (Edge e : S) {
			int u = e.start; int v = e.end;
			if (s.find(u) == s.find(v)) continue;
			T.add(e);
			s.union(u, v);
		}
		// 오름차순으로 출력하기 쉽도록 정점별로 우선순위 큐를 저장
		ArrayList<PriorityQueue<Integer>> R = new ArrayList<>(N);
		for (int i = 0; i <= N; i++) R.add(new PriorityQueue<>());
		for (Edge e : T) {
			R.get(e.start).add(e.end);
			R.get(e.end).add(e.start);
		}
		for (int i = 1; i <= N; i++) {
			bw.append(R.get(i).size()).append(" ");
			while (!R.get(i).isEmpty()) bw.append(R.get(i).poll()).append(" ");
			bw.append("\n");
		}
		System.out.print(bw);
	}

}

class DisjointSet {
	int[] parent, rank;
	
	DisjointSet(int n) { 
		parent = new int[n];
		for (int i = 0; i < n; i++) parent[i] = i;
		rank = new int[n];
	}
	
	void union(int u, int v) {
		u = find(u); v = find(v);
		if (u == v) return;
		if (rank[u] > rank[v]) { int temp = u; u = v; v = temp; }
		parent[u] = v;
		if (rank[u] == rank[v]) rank[v]++;
	}
	
	int find(int u) {
		if (parent[u] == u) return u;
		return parent[u] = find(parent[u]);
	}
	
}

class Edge implements Comparable<Edge> {
	int start, end, weight;
	
	Edge(int u, int v, int w) { start = u; end = v; weight = w; }
	
	@Override
	public int compareTo(Edge o) { return weight - o.weight; }
	
}

핑크 플로이드는 유명한 영국의 록 밴드 이름입니다. 사실 PS하는 사람이면 플로이드 하면 플로이드-워셜 알고리즘이 떠오르지만 세계적으로는 이 쪽이 더 널리 알려져 있습니다.