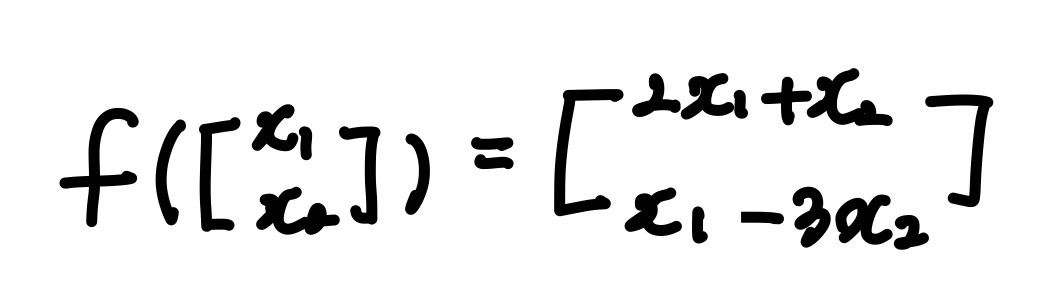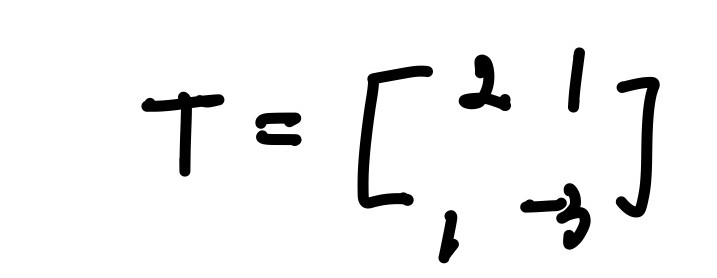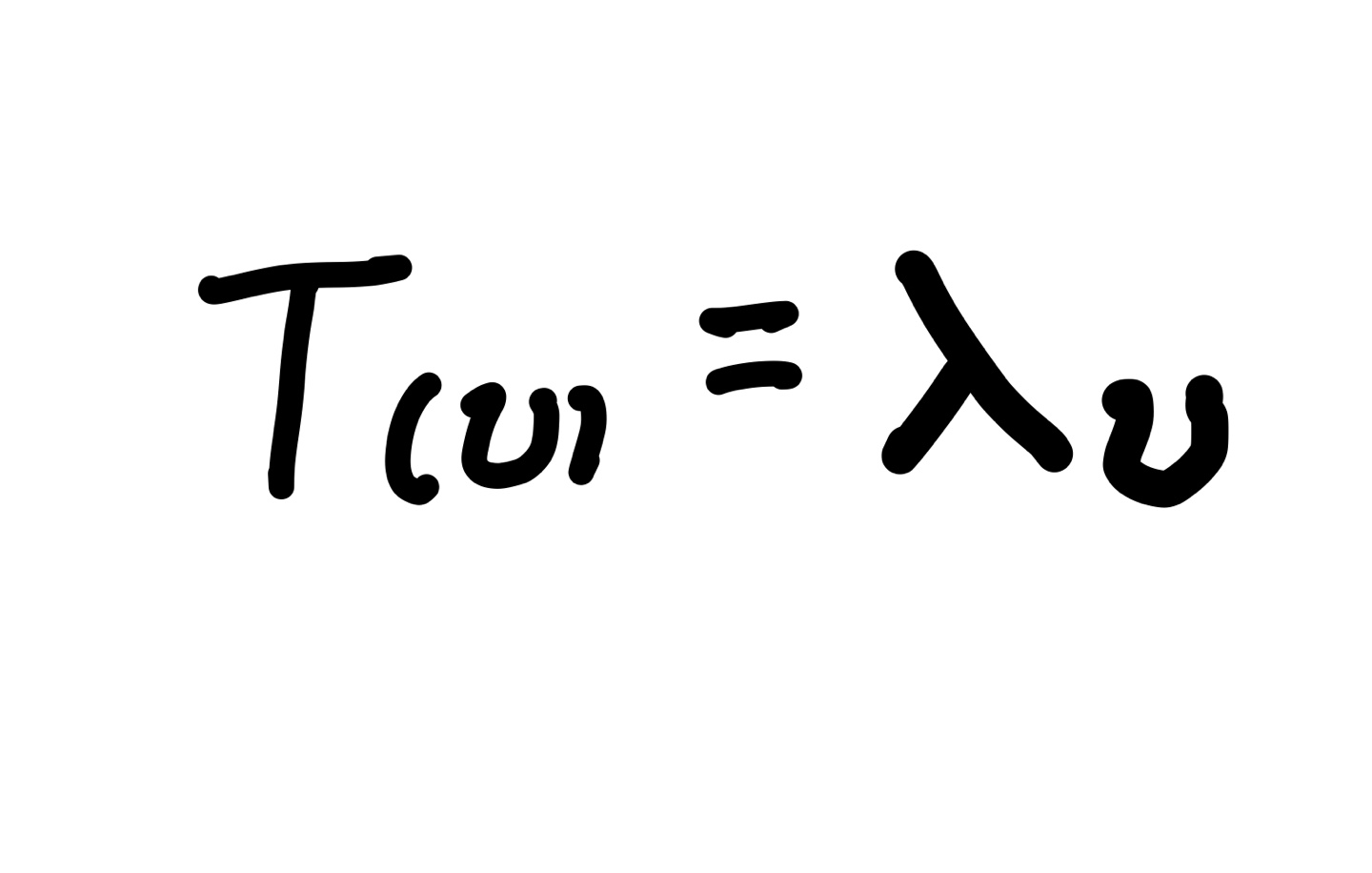DAY13

Vector transformation

선형 변환은 임의의 두 벡터를 더하거나 혹은 스칼라 값을 곱하는 것을 의미

벡터변환으로써의 매트릭스-벡터의 곱

[x1,x2]를 [2x1 +x2, x1-3x2]로 변환한다:

$x_1 \cdot \hat{i} + x_2 \cdot \hat{j}$
분리된 각 유닛벡터는 transformation를 통해서 각각

• $2x_1$, $x_1$과
• $x_2$, $-3x_2$라는 결과가 나와야 함
  이를 매트릭스의 형태로 합치게 되면:
  
  이 매트릭스(T)를 처음 벡터 [x1,x2]에 곱했을 경우 transformation이 원하는 대로 이루어진다는 것을 알 수 있습니다

Transformation은 matrix를 곱하는 것을 통해, 벡터(데이터)를 '다른 위치로 옮긴다' 라는 의미를 가지고 있습니다

고유벡터 and 고유값

고유벡터: transformation에 영향을 받지 않는 회전축, (혹은 벡터)을 공간의 고유벡터 (Eigenvector)라고 부릅니다.
transformation에 대해서 크기만 변하고 방향을 변지 않는 벡터

고유값: 변화하는 크기는 스칼라로 인해 변화하는데, 이 특정 스칼라 값

• eigenvector와 eigenvalue는 항상 쌍을 이루고 있다
• $\lambda$ 로 표기
  

라이브러리로 고유값 (Eigenvalue), 고유벡터 (Eigenvector)

출처: https://rfriend.tistory.com/380 [R, Python 분석과 프로그래밍의 친구 (by R Friend)]

고유값을 왜 배울까?

어떤 목적, 어떤 transformation 하느냐에 따라 고유값이 선택지가 될 수 있음
그렇다면 어떤목적으로 쓰일까?

고차원의 문제 (The Curse of Dimensionality)

피쳐의 수가 많은 (100 혹은 1000개 이상의) 데이터셋을 모델링하거나 분석할때에 생기는 여러 문제점들을 의미

• 데이터 다루는데 너무 어렵고 많은 피쳐가 실제적으로 의미가 없을 수도 있다.(비효율적)
• overfitting의 문제

Dimension Reduction

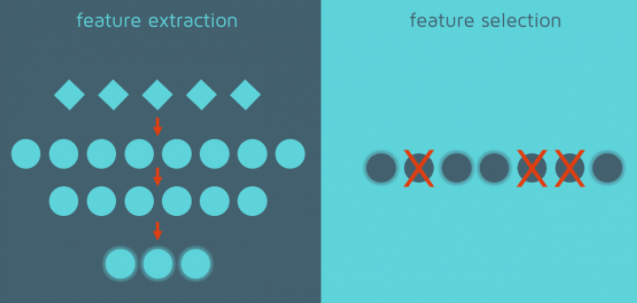
Feacture Selection

데이터셋에서 제일 다양하게 분포되어있는 (1개의) feature를 사용하는 것입니다. 이처럼 Feature Selection이란 데이터셋에서 덜 중요한 feature를 제거 하는 방법을 의미

Feature Extraction

Feature Extraction이란 앞서 Feature engineering 와 같이

• 기존에 있는 Feature or 그들을 바탕으로 조합된 Feature를 사용
• 예) PCA

Principal Component Analysis (PCA)

• 고차원 데이터를 효과적으로 분석 하기 위한 기법
• 낮은 차원으로 차원축소
• 고차원 데이터를 효과적으로 시각화 + clustering
• 원래 고차원 데이터의 정보(분산)를 최대한 유지하는 벡터를 찾고, 해당 벡터에 대해 데이터를 (Linear)Projection

Quiz .예를 들어 x,y중에 1개만 분석한다면 어떤 것을 사용해야할까?

: 분산이 더 큰 피쳐를 사용

from sklearn.preprocessing import StandardScaler, Normalizer
from sklearn.decomposition import PCA
scaler = StandardScaler()
Z = scaler.fit_transform(X) # Standardized Data
pca = PCA(2) #2개로 축소
pca.fit(Z)  # Eigenvectors, Eigenvalues
B = pca.transform(Z)  #Projected Data

pca.explainedvariance_ratio 출처1 출처2

더 참고할 만한 자료
https://www.youtube.com/watch?v=FgakZw6K1QQ
https://m.blog.naver.com/tjdrud1323/221720259834

---

N133

seaborn으로 scatterplot 만들기

sns.scatterplot(data=df, x='x축 이름',y='y축 이름, hue=' 범례나 종류가 될 행이름', s=100) #s는 점의 크기

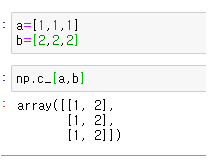
원소끼리 2개의 축(column)으로 연결하여 2차원 배열로 만들기:np. c

[출처]https://blog.naver.com/skchajie/222101091469 [Python] Numpy 이용하기 : np.r , np.c_|작성자 지잉