
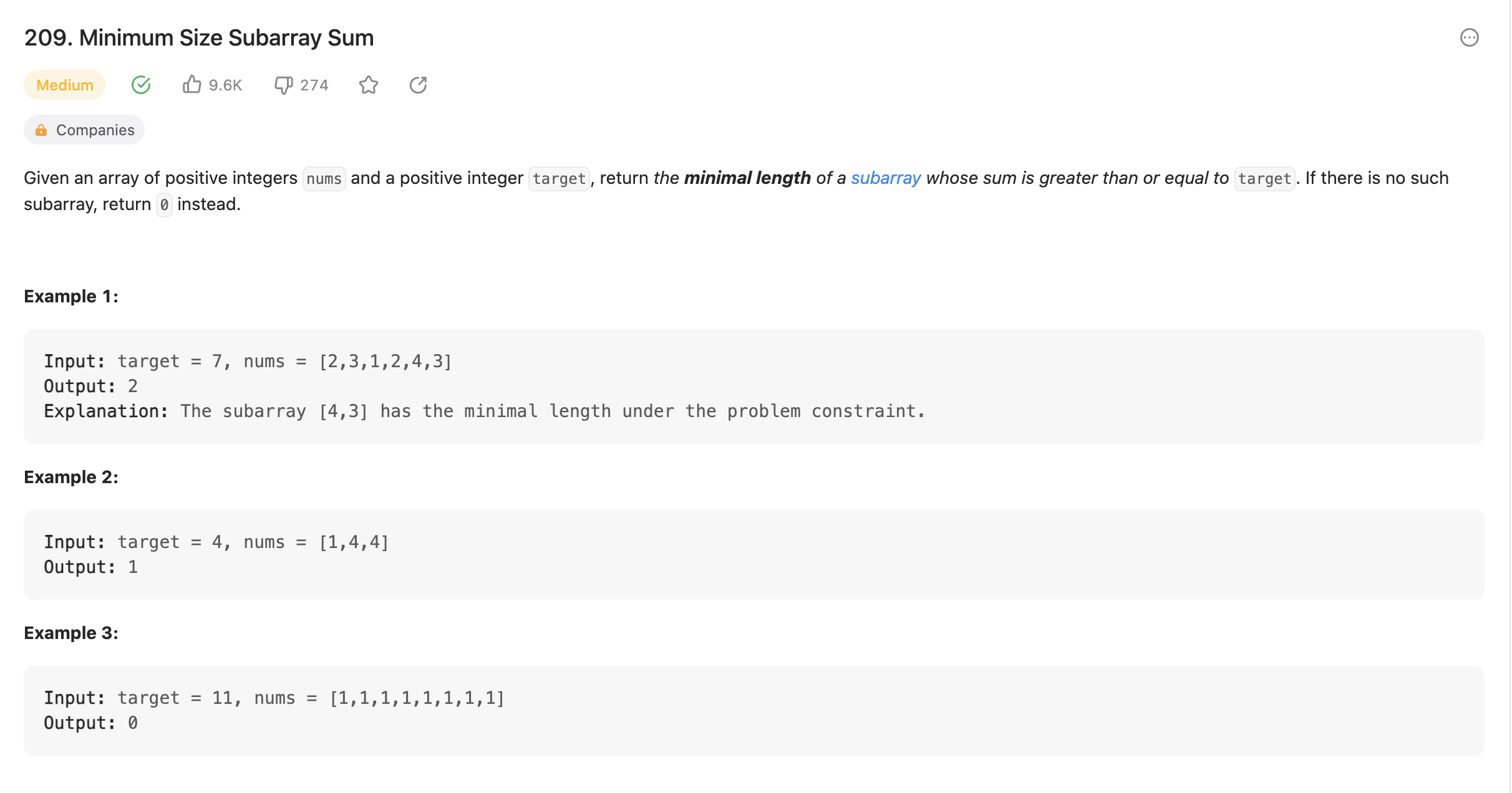
[Leetcode] 209. Minimum Size Subarray Sum
이번 알고리즘은 처음 들어보는 알고리즘으로 푸는 방식이었다.
알고리즘 자체는 아주 쉽다.
Sliding Window
슬라이딩 윈도우 알고리즘은 일정한 범위(window)를 유지하면서 이동하는 것을 의미한다.
- Fixed Window
- Variable Window
이 알고리즘은 고정인가 아닌가로 두 개의 분류로 나뉘게 된다.
Fixed Window
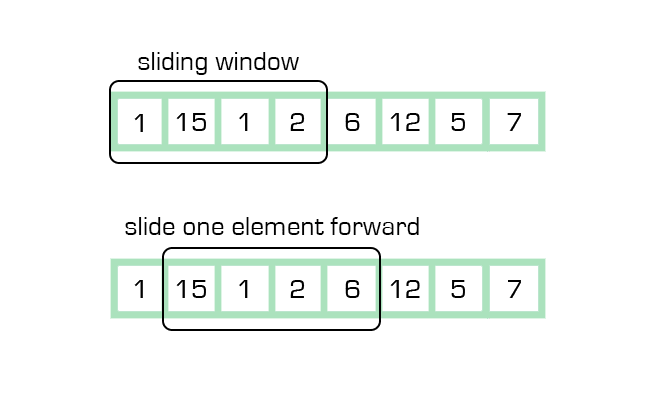
고정된 sliding window에서는 부분 배열의 크기 k 에서 최대 또는 최소합을
구하는 문제에 적용될 수 있다.
위의 사진처럼 k=4 라고 하였을 때
0번 째의 인덱스에서 3번 인덱스까지 요소 4개를 포함시키고
그 합을 구한 뒤 tmp 에 저장한다.
그 다음은 크기는 유지하되 인덱스만 한 칸 옮겨서 요소의 합을 구하고
저장했던 tmp 와 비교후 더 큰 값을 새로 저장하거나 유지한다.
Variable Window
가변길이의 경우는 어떤 조건에 부합하는 부분 배열중 가장 짧은 부분 배열을
구하는 문제에 적용될 수 있다.

target 값은 부분 배열의 합의 최솟값을 나타내며
적어도 합이 7 이상을 만족하는 배열중 가장 짧은 배열을 찾아보자.
class Solution:
def minSubArrayLen(self, target: int, nums: List[int]) -> int:
num_len = len(nums)
ans = num_len + 1
i = 0
j = 0
s = 0
ext = -1
while (i <= j):
if (ext != j):
s += nums[j]
print(i,j,s)
if (s >= target):
ans = min(ans, j - i + 1)
s -= nums[i]
i += 1
ext = j
else:
if (j != num_len - 1):
j += 1
else:
s -= nums[i]
i += 1
if (ans == num_len + 1): return 0
return ansindex를 하나씩 순회하며 범위를 넓혀가는데 만약 target 보다 크다면
진행하던 j 인덱스를 멈추고 i 인덱스만 증가시켜 범위를 좁힌다.
그렇게 target 보다 합이 작아지는 순간 다시 j 를 증가시키면 앞으로 나아간다.
