[Leetcode] 5 - Longest Palindromic Substring
대표적인 DB문제로
문자열에서 뒤집어도 똑같은 가장 긴 문자열을 찾는 문제이다.
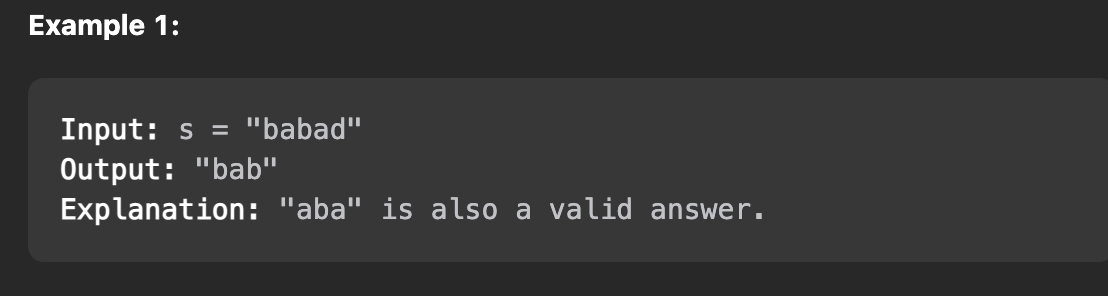 예제가 쉽게 적혀있어서 처음에는 크게 고민하지 않았는데 단순히 한 문자마다 문자열의 끝부터 하나하나 확인하는 행위는 실행해보지 않아도 시간초과가 날 것임을 알 수 있다.
예제가 쉽게 적혀있어서 처음에는 크게 고민하지 않았는데 단순히 한 문자마다 문자열의 끝부터 하나하나 확인하는 행위는 실행해보지 않아도 시간초과가 날 것임을 알 수 있다.
그래서 조금 더 고민하다보니 더욱 단순한 진실을 마주할 수 있었다.
결국 앞 뒤로 똑같다는 것은 중심이 되는 문자가 반드시 존재한다는 것.
예를들어 홀수인 펠린드롬 문자열은 "abcba"인데 "bcb가 중심이 되고,
짝수에서는 "abccba" 즉 "cc"가 중심 문자열이 된다.
그렇다면 문제는 아주 간단해진다. 반복되는 중심부만 찾으면 그 중심부에서 범위를 확장시켜버리면 되는 것이다.
ef longestPalindrome(self, s):
index, l = 0, 0
s_len = len(s)
if (s_len <= 1):
return s
for j in range(s_len):
if (s[j - l : j + 1] == s[j - l : j + 1][::-1]):
index, l = j - l, l + 1
elif (j - l > 0 and s[j - l - 1 : j + 1] == s[j - l - 1 : j + 1][::-1]):
index, l = j - l - 1, l + 2
return s[index: index + l]index = 펠린드롬이 시작되는 인덱스 위치
ㅣ = 펠린드롬의 문자열의 길이
코드에서 중요한 핵심은 for문 다음에 위치한 4줄 문장이다.
if-elif 문으로 "ABA", "AA"같은 두 경우를 모두 체크한다.
예시로 들어서 설명하는것이 이해가 더욱 빠르니
"efgdabcba"로 예시를 들어보겠다.
-
j = 0 일 때
s[0 : 1] == s[0 : 1][::-1]=> "e" == "e"는 참이므로
index = j - l= 0,l = l + 1= 1
로 수정한다. -
j = 1 일 때
s[0 : 2] == s[0 : 2][::-1]=> "ef" == "fe"는 거짓이므로 다음 코드로 넘어간다.
0 > 0은 거짓이므로 아무런 행위없이 다음으로 넘어간다. -
j = 2 일 때
s[1 : 3] == s[1 : 3][::-1]=> "fg" == "gf"는 거짓이므로 다음 코드로 넘어간다.
1 > 0 and s[0 : 3] == s[0 : 3][::-1]=> "efg" == "gfe"는 거짓이므로 아무런 행위없이 다음으로 넘어간다.
.
.
.
-
j = 7 일 때
s[6 : 8] == s[6 : 8][::-1]=> "cb" == "bc"는 거짓이므로 다음 코드로 넘어간다.
6 > 0 and s[5 : 8] == s[5 : 8][::-1]=> "bcb" == "bcb"는 참이므로
index = j - l= 5,l = l + 2= 3
으로 수정한다. -
j = 8 일 때
s[5 : 9] == s[5: 9][::-1]=> "bcba" == "abcb"는 거짓이므로 다음 코드로 넘어간다.
5 > 0 and s[4 : 9] == s[4 : 9][::-1]=> "abcba" == "abcba"는 참이므로
index = j - l= 4,l = l + 2= 5
으로 수정한다.
그래서 정답은 길이가 5인 "abcba"가 되는것이고, 로직 동작원리를 보면
펠린드롬 문자열이 발견되면 그 길이만큼 l을 증가시킨다.
j가 증가하더라도 펠린드롬 문자열을 발견하게 되면 l이 증가하여 검사하는 범위가 확장되게 되고, 확장한 범위가 펠린드롬 문자열이 아니라면
변경된 l크기 그대로 문자열 끝까지 검사를 진행하게 되는것이다.
여기서 핵심은 펠린드롬 문자열이 발견될 때마다 범위가 확장되야하며
펠린드롬문자의 크기는 반드시 전체 문자열의 크기와 같거나 작기 때문에
0 ~ n까지 순회하는것만으로도 찾을 수 있는것이다.

