시간 복잡도(Time Complexity)

알고리즘이란?

'문제를 어떤 식으로 푸는 것이 최선인가'로 정의될 수 있다.
< 알고리즘의 순서 >
1. 문제를 이해하세요
2. 문제를 어떻게 해결할 수 있을지에 대한 전략을 세워 보세요
3. 문제를 코드로 옮겨 보세요

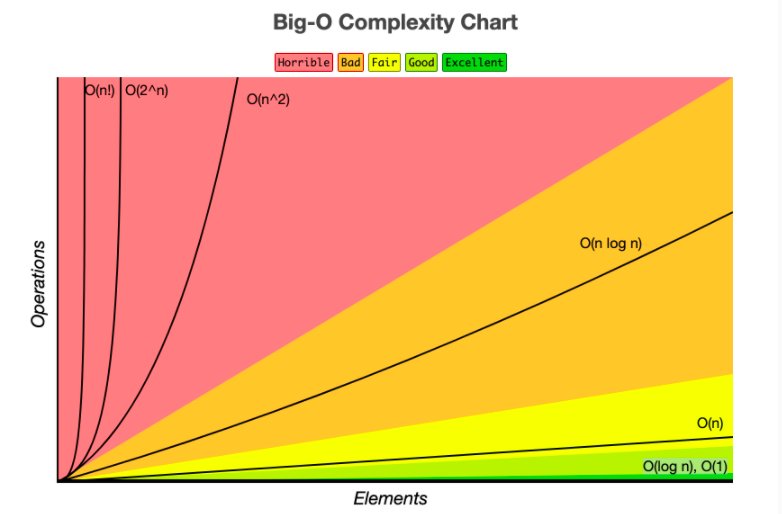
시간 복잡도란?

효율적인 알고리즘을 구현한다는 것이며, 즉 입력값이 커짐에 따라 증가하는 시간의 비율을 최소화한 알고리즘을 구현한 것이라고 할 수 있다.

Big-O 표기법

빅오 표기법은 불필요한 연산을 제거하여 알고리즘분석을 쉽게 할 목적으로 사용된다.

시간 복잡도를 표기하는 방법 중엔,

• Big-O : 최악의 경우
• Big-Ω : 최상의 경우
• Big-θ : 평균의 경우

이중 가장 흔히 사용 되는 것은 Big-O 표기법인데 최악의 경우가 발생하지 않기를 바라며 시간을 계산하는 것보단, 최악의 경우도 고려하여 대비O(n2)하는 것이 바람직하다고 할 수 있습니다.

Big-O 표기법의 종류

1. O(1) (constant complexity)

상수 시간 : 문제를 해결하는데 오직 한 단계만 처리함.
입력값이 증가해도 시간은 늘어나지 않음을 의미

2. O(n) (linear complexity)
   직선적 시간 : 문제를 해결하기 위한 단계의 수와 입력값 n이 1:1 관계를 가짐.
   입력값이 증가함에 따라 시간 또한 같은 비율로 증가하는 것

3. O(log n) (logarithmic complexity)
   로그 시간 : 문제를 해결하는데 필요한 단계들이 연산마다 특정 요인에 의해 줄어듬.
   Big-O표기법중 O(1) 다음으로 빠른 시간 복잡도를 가진다.

4. O(n2) (quadratic complexity)
   2차 시간 : 문제를 해결하기 위한 단계의 수는 입력값 n의 제곱.
   입력값이 증가함에 따라 시간이 그의 제곱수의 비율로 증가하는 것

5. O(2n) (exponential complexity)
   지수 시간 : 문제를 해결하기 위한 단계의 수는 주어진 상수값 C 의 n 제곱.
   Big-O표기법 중 가장 느린 시간 복잡도

시간 복잡도 구하기

• 하나의 루프를 사용하여 단일 요소 집합을 반복 하는 경우 : O (n)
• 컬렉션의 절반 이상 을 반복 하는 경우 : O (n / 2) -> O (n)
• 두 개의 다른 루프를 사용하여 두 개의 개별 콜렉션을 반복 할 경우 : O (n + m) -> O (n)
• 두 개의 중첩 루프를 사용하여 단일 컬렉션을 반복하는 경우 : O (n²)
• 두 개의 중첩 루프를 사용하여 두 개의 다른 콜렉션을 반복 할 경우 : O (n * m) -> O (n²)
• 컬렉션 정렬을 사용하는 경우 : O(n*log(n))