🔥[99클럽 코테 스터디] 36일차 TIL - 전력망을 둘로 나누기

⏳문제

n개의 송전탑이 전선을 통해 하나의 트리 형태로 연결되어 있습니다. 당신은 이 전선들 중 하나를 끊어서 현재의 전력망 네트워크를 2개로 분할하려고 합니다. 이때, 두 전력망이 갖게 되는 송전탑의 개수를 최대한 비슷하게 맞추고자 합니다.

송전탑의 개수 n, 그리고 전선 정보 wires가 매개변수로 주어집니다. 전선들 중 하나를 끊어서 송전탑 개수가 가능한 비슷하도록 두 전력망으로 나누었을 때, 두 전력망이 가지고 있는 송전탑 개수의 차이(절대값)를 return 하도록 solution 함수를 완성해주세요.

🚨제한 사항

• n은 2 이상 100 이하인 자연수입니다.
• wires는 길이가 n-1인 정수형 2차원 배열입니다.
• wires의 각 원소는 [v1, v2] 2개의 자연수로 이루어져 있으며, 이는 전력망의 v1번 송전탑과 v2번 송전탑이 전선으로 연결되어 있다는 것을 의미합니다.
• 1 ≤ v1 < v2 ≤ n 입니다.
• 전력망 네트워크가 하나의 트리 형태가 아닌 경우는 입력으로 주어지지 않습니다.

📃입출력 예

n	wires	result
9	[[1,3],[2,3],[3,4],[4,5],[4,6],[4,7],[7,8],[7,9]]	3
[[1,2],[2,3],[3,4]]	0
7	[[1,2],[2,7],[3,7],[3,4],[4,5],[6,7]]	1

입출력 예 #1

• 다음 그림은 주어진 입력을 해결하는 방법 중 하나를 나타낸 것입니다.
  

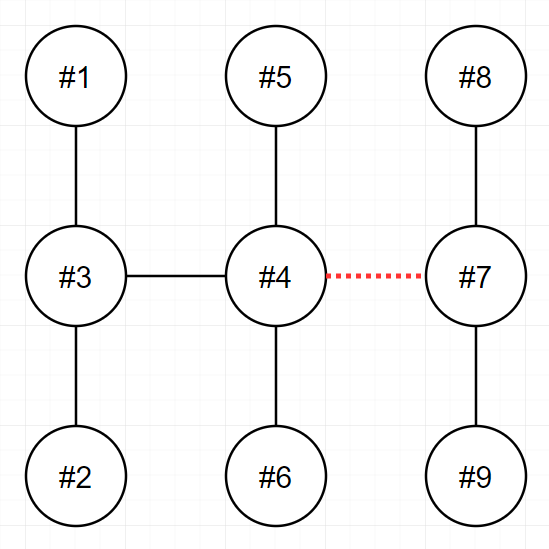
• 4번과 7번을 연결하는 전선을 끊으면 두 전력망은 각 6개와 3개의 송전탑을 가지며, 이보다 더 비슷한 개수로 전력망을 나눌 수 없습니다.

• 또 다른 방법으로는 3번과 4번을 연결하는 전선을 끊어도 최선의 정답을 도출할 수 있습니다.

입출력 예 #2

• 다음 그림은 주어진 입력을 해결하는 방법을 나타낸 것입니다.
  

• 2번과 3번을 연결하는 전선을 끊으면 두 전력망이 모두 2개의 송전탑을 가지게 되며, 이 방법이 최선입니다.

입출력 예 #3

• 다음 그림은 주어진 입력을 해결하는 방법을 나타낸 것입니다.
  

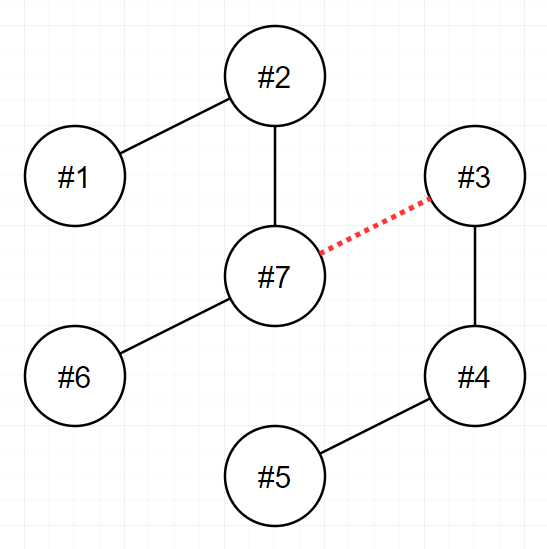
• 3번과 7번을 연결하는 전선을 끊으면 두 전력망이 각각 4개와 3개의 송전탑을 가지게 되며, 이 방법이 최선입니다.

---

✏️풀이

이 문제에서 요구하는 것은 끊은 전선을 기준으로 나누어진 두 그룹 안에서의 송전탑 개수를 각각 파악해 그 차이가 최소가 되는 지점이다.
따라서 나는 송전탑의 전선을 하나씩 끊어보면서 나누어진 두 그룹안에서의 송전탑 개수를 각각 BFS를 통해 구해보기로 하였다.

👾최종 코드

import java.util.*;

class Solution {
    static int[][] graph;
    static boolean[] visited;

    public static int solution(int n, int[][] wires) {
        int answer = wires.length;

        for (int i = 0; i < wires.length; i++) {
            graph = new int[n + 1][n + 1]; // 그래프 초기화
            visited = new boolean[n + 1]; // 방문 여부 초기화

            // 송전탑 연결 정보 저장
            for (int j = 0; j < wires.length; j++) {
                // i번째 연결을 제외하고 저장
                if (wires[j] != wires[i]) {
                    graph[wires[j][0]][wires[j][1]] = 1;
                    graph[wires[j][1]][wires[j][0]] = 1;
                }
            }

            // 두 개의 출발지로 나누기
            int start1 = wires[i][0]; // 첫 번째 출발지
            int start2 = wires[i][1]; // 두 번째 출발지
            
            int sum1 = bfs(start1, n); // 첫 번째 송전탑 개수
            int sum2 = bfs(start2, n); // 두 번째 송전탑 개수

            // sum1 - sum2 최소값 업데이트
            if (answer > Math.abs(sum1 - sum2)) {
                answer = Math.abs(sum1 - sum2);
            }

        }
        return answer;
    }

	// bfs
    public static int bfs(int start, int n) {
        Queue<Integer> queue = new LinkedList<>(); // bfs를 위한 큐 생성
        queue.offer(start); // 시작점
        visited[start] = true; // 방문 여부
        int count = 1; // 시작 송전탑 포함

        while (!queue.isEmpty()) {
            int current = queue.poll();
            for (int i = 1; i <= n; i++) {
                if (graph[current][i] == 1 && !visited[i]) {
                    visited[i] = true;
                    queue.offer(i);
                    count++;
                }
            }
        }
        return count;
    }
}

👻코드 설명

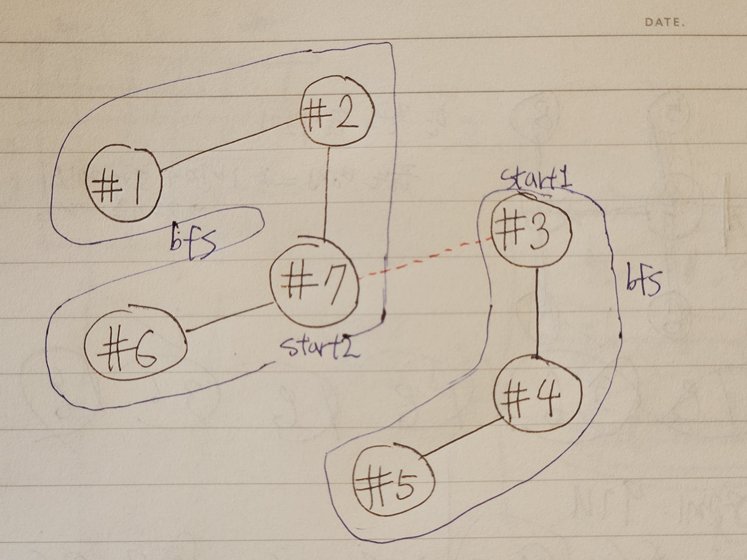
1. 송전탑 연결 정보를 저장한다.

2. wires에 저장되어 있는 연결 정보 중 i번째 연결을 제외하고 인접 행렬 graph에 저장한다.

3. 제외한 연결의 양 끝 노드를 start1과 start2에 각각 저장한다.

4. 두 노드를 기준으로 bfs를 각각 수행해 각 그룹 안에 있는 송전탑의 개수를 구한다.

5. 두 그룹의 각 송전탑 개수 sum1, sum2의 차이의 최소값을 answer에 저장한다.

---

🔗문제 링크
💻Repository