🔥[99클럽 코테 스터디] 41일차 TIL - Unique Paths II

⏳문제

You are given an m x n integer array grid. There is a robot initially located at the top-left corner (i.e., grid[0][0]). The robot tries to move to the bottom-right corner (i.e., grid[m - 1][n - 1]). The robot can only move either down or right at any point in time.

An obstacle and space are marked as 1 or 0 respectively in grid. A path that the robot takes cannot include any square that is an obstacle.

Return the number of possible unique paths that the robot can take to reach the bottom-right corner.

The testcases are generated so that the answer will be less than or equal to $2 * 10^9$.

📄입출력 예

입출력 예 #1

Input : obstacleGrid = [[0,0,0],[0,1,0],[0,0,0]]
Output : 2
Explanation : There is one obstacle in the middle of the 3x3 grid above.
There are two ways to reach the bottom-right corner:
1. Right -> Right -> Down -> Down
2. Down -> Down -> Right -> Right

입출력 예 #2

Input : obstacleGrid = [[0,1],[0,0]]
Output : 1

🚨제한 사항

• m == obstacleGrid.length
• n == obstacleGrid[i].length
• 1 <= m, n <= 100
• obstacleGrid[i][j] is 0 or 1.

---

✏️풀이

이 문제는 어제 풀었던 Unique Paths 문제와 크게 다르지 않다.
가장 큰 차이점은 장애물이 추가되었다는 것이다.

장애물을 피해가는 방법은 간단하다.
경로의 수를 탐색해나가는 과정은 기존의 점화식과 동일한데,

grid[m][n] = grid[m-1][n] + grid[m][n-1]

장애물은 0으로 표시만 해주면 된다.

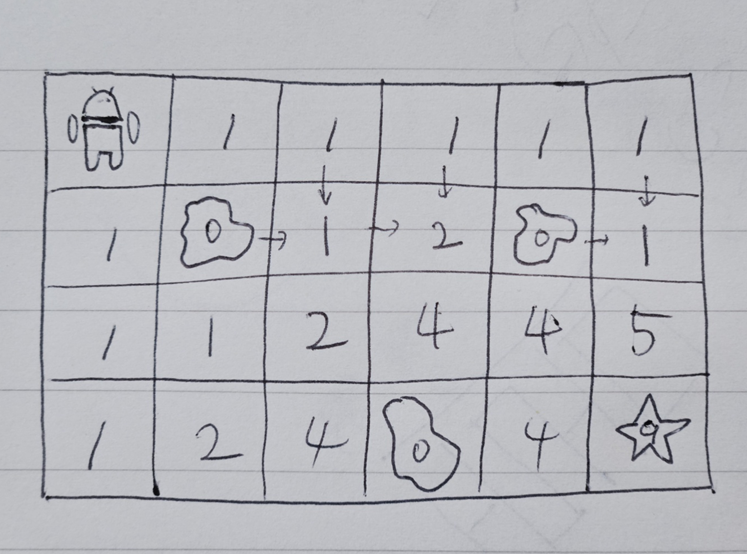
여기서 주의해야 할 점은, 장애물의 위치이다.
장애물이 출발지 [0, 0]에 있는 경우와 0번째 행 또는 0번째 열에 있는 경우를 고려해야 한다.

그리드 초기화

    // 출발지 위치에 장애물이 있는 경우
    if (obstacleGrid[0][0] == 1) {
    	return 0;
    }

    obstacleGrid[0][0] = 1;
	// 0열 초기화
    for (int i = 1; i < m; i++) {
        // 장애물은 0으로 저장
        if (obstacleGrid[i][0] == 1) {
            obstacleGrid[i][0] = 0;
        }
        else {
            obstacleGrid[i][0] = obstacleGrid[i-1][0];
        }
    }

    // 0행 초기화
    for (int i = 1; i < n; i++) {
        if (obstacleGrid[0][i] == 1) {
            obstacleGrid[0][i] = 0;
        }
        else {
            obstacleGrid[0][i] = obstacleGrid[0][i-1];
        }
    }

그리드 초기화는 0행과 0열에 모두 1을 저장하는 것인데,
출발지에 장애물이 위치해 있는 경우는 무조건 최종 반환 값이 0이기 때문에 이를 처리해 준다.

그리고, 0열과 0행을 초기화할 때 장애물은 0으로 저장해주고, 장애물이 아니라면, 이전 값을 그대로 저장함으로써, 장애물의 위치를 고려해 초기화를 해 주어야 한다.

경로 수 탐색

        // 경로 수 탐색
        for (int i = 1; i < m; i++) {
            for (int j = 1; j < n; j++) {
                if (obstacleGrid[i][j] == 1) {
                    obstacleGrid[i][j] = 0; // 장애물 표시
                }
                else {
                    // 경로 수 업데이트
                    obstacleGrid[i][j] = obstacleGrid[i-1][j] + obstacleGrid[i][j-1];
                }
            }
        }

이제 경로의 수를 [1,1]좌표부터 기존의 점화식을 이용해 구해나가면 된다.
단, 장애물을 발견 시 해당 원소 값에 0을 저장한다.

👾전체 코드

public static int uniquePathsWithObstacles(int[][] obstacleGrid) {
    int m = obstacleGrid.length; // 세로 길이
    int n = obstacleGrid[0].length; // 가로 길이

    // 출발지 위치에 장애물이 있는 경우
    if (obstacleGrid[0][0] == 1) {
        return 0;
    }

    obstacleGrid[0][0] = 1;

    // 0열 초기화
    for (int i = 1; i < m; i++) {
        // 장애물은 0으로 저장
        if (obstacleGrid[i][0] == 1) {
            obstacleGrid[i][0] = 0;
        }
        else {
            obstacleGrid[i][0] = obstacleGrid[i-1][0];
        }
    }

    // 0행 초기화
    for (int i = 1; i < n; i++) {
        if (obstacleGrid[0][i] == 1) {
            obstacleGrid[0][i] = 0;
        }
        else {
            obstacleGrid[0][i] = obstacleGrid[0][i-1];
        }
    }

    // 경로 수 탐색
    for (int i = 1; i < m; i++) {
        for (int j = 1; j < n; j++) {
            if (obstacleGrid[i][j] == 1) {
                obstacleGrid[i][j] = 0; // 장애물 표시
            }
            else {
                // 경로 수 업데이트
                obstacleGrid[i][j] = obstacleGrid[i-1][j] + obstacleGrid[i][j-1];
            }
        }
    }

    return obstacleGrid[m-1][n-1];
}

---

🔗문제 링크
💻Repository