자료구조 기초

1. 자료(Data)
2. 자료구조(Data Structure)
3. 시간복잡도

1. 자료(Data)

자료란, 문자, 숫자, 소리, 그림, 영상 등 특정 형태로 된 의미를 지니는 단위를 말한다. 만약 이러한 단위가 무작위로 나열되어 있다면 어떨까? 만약 책을 읽는데, 그 책의 원래 내용을 단어 단위로 뒤섞어서 책을 구성했다고 생각해보자. 이 책이 무엇을 전하고 있는지 판단할 수 있을까? 따라서 우리는 자료를 잘 가공하여 원하는 정보를 얻을 수 있도록 구조화할 필요가 있다.

2. 자료구조(Data Structure)

자료구조란 자료(Data)의 집합을 의미한다. 데이터를 효율적으로 저장하고 관리하며 처리하는 방법을 다루는 컴퓨터 과학의 분야를 나타낸다. 자료구조는 데이터의 종류와 사용 목적에 다라 다양한 방식으로 구현될 수 있으며, 이를 통해 알고리즘의 성능을 개선하고 프로그램을 효율적으로 실행할 수 있습니다.

2-1. 자료구조의 선택 기준

• 데이터의 처리시간
• 데이터의 크기
• 데이터의 활용 빈도
• 데이터의 갱신 정도
• 프로그램의 용이성

2-2. 자료구조의 특징

1. 효율성(Efficiency)

• 알고리즘이 데이터를 처리하는데에 걸리는 시간과 사용하는 메모리의 양을 나타낸다. 효율적인 자료구조를 사용하면 프로그램의 성능을 향상 시킬 수 있습니다. 또한 시간 복잡도와 공간 복잡도를 고려하여 자료구조를 선택하고 설계함으로써, 더 효율적인 알고리즘을 구현할 수 있습니다.

2. 추상화(Abstraction)

• 구체적인 구현과 상세 내용을 숨기고, 간단한 인터페이스를 제공하여 사용자가 자료구조를 쉽게 활용 할 수 있게 합니다. 이를 통해 사용자는 복잡한 내부 구현을 알 필요 없이, 자료구조의 기능과 연산만을 사용할 수 있습니다. 추상화는 사용자에게 편의성과 쉬운 사용을 제공하며, 코드의 가독성을 높이고 유지보수를 용이하게 합니다.

3. 재사용성(Reusable)

• 자료구조는 여러 알고리즘과 프로그램에서 재사용될 수 있습니다. 특정 자료구조가 한 알고리즘에서 유용하게 쓰인다면, 다른 알고리즘에서도 활용 가능합니다. 또한, 자료구조의 추상화를 통해 구현의 상세 내용을 감추기 때문에, 다른 프로그램에서도 자료구조를 쉽게 사용하고 재사용할 수 있습니다. 재사용성은 코드의 중복을 줄이고, 개발 시간을 단축시키는 데에 도움이 됩니다.

2-3. 자료구조의 종류

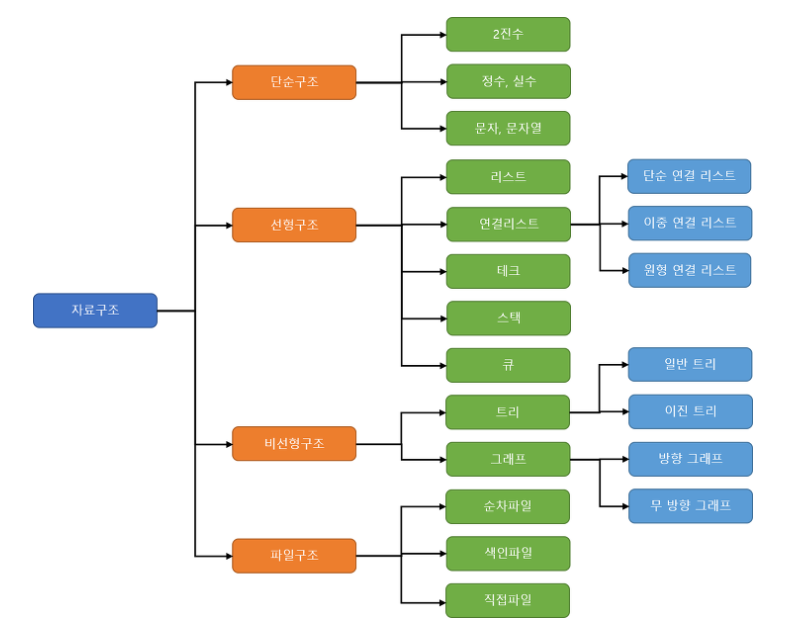
1. 단순구조(Simple Structure): T/F, 정수, 실수, 문자 및 문자열과 같이 컴퓨터가 기본적으로 제공하는 자료형
2. 선형구조(Linear Structure): 데이터들이 일렬로 쭉 저장되어 있는 형태
3. 비선형구조(Non-Linear Structure): 데이터가 트리 형태로 저장되어 있다고 생각하고 사용하는 자료구조
4. 파일구조(File Structure): 다양한 자료구조의 데이터를 파일에 저장하는 방식

3. 시간복잡도

알고리즘의 복잡도를 판단하는 척도는 시간 복잡도와 공간 복잡도가 있다.
그 중 시간 복잡도는 알고리즘 내 연산의 횟수와 밀접한 관련이 있다.

3-1. 시간 복잡도 표기법

• Big-O(빅 오) 표기법 알고리즘 최악의 실행 시간을 표기한다. 가장 많이 사용하는 표기법이다. 최소한 보장되는 성능을 표기하기 때문에 가장 일반적으로 사용한다.
• Big-Ω(빅 오메가) 표기법 알고리즘 최상의 실행 시간을 표기한다.
• Big-θ(빅 세타) 표기법 알고리즘 평균 실행 시간을 표기한다.

3-2. 빅오 표기법(big-O notation) 특징

1. 상수항을 무시
   어떤 알고리즘이 O(N+5)의 복잡도를 가졌으면 상수를 생략해 O(N)으로 표기한다.
2. 계수 무시
   어떤 알고리즘이 O(3N)의 복잡도를 가졌으면 계수를 생략해 O(N)으로 표기한다.
3. 최고차항만 표기
   어떤 알고리즘이 O(3N^3+2N^2+N+5)의 복잡도를 가졌으면 O(N^3)으로 표기한다.

3-3. 빅오 표기법(big-O notation) 종류

실행 속도 O(1) < O(log N) < O(N) < O(N log N) < O(N^2) < O(2^N)

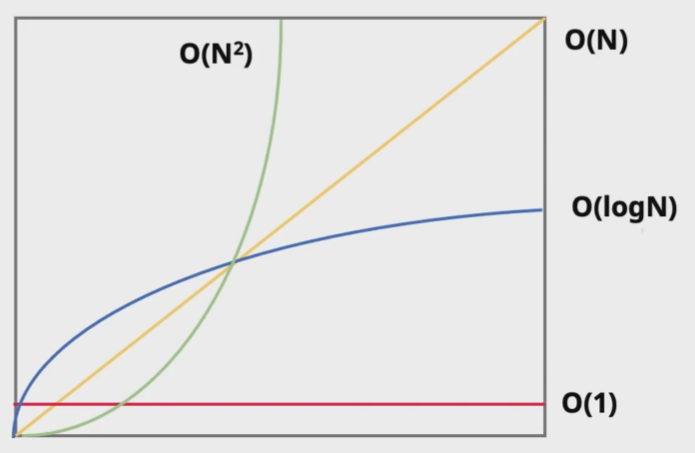
1. O(1)

• 입력 데이터의 크기와 상관없이 항상 일정한 시간이 걸리는 알고리즘
• Ex) Hash

2. O(N)

• 입력 데이터의 크기에 비례해서 시간이 소요되는 알고리즘
• Ex) 1중 For문

3. O(N^2)

• O(N)의 알고리즘과 O(log N)의 알고리즘이 중첩된 형태
• Ex) 2중 For 문, 삽입/거품/선택 정렬

4. O(logN)

• 연산이 한 번 실행될 때 마다 데이터의 크기가 절반 감소하는 알고리즘
• Ex) Binary Search 알고리즘, Tree 형태 자료구조 탐색

5. O(NlonN)

• O(N)의 알고리즘과 O(log N)의 알고리즘이 중첩된 형태
• Ex) 퀵 / 병합 / 힙 정렬