1517번 : 버블 소트 - Python

문제

https://www.acmicpc.net/problem/1517

풀이

이 문제를 버블정렬를 구현하면서 count한다면 시간초과가 난다.
이 문제는 0~(i-1)의 원소들 중 arr[i]보다 작은 원소들의 개수를 카운트 한다.
이것을 병합정렬을 구현해서 왼쪽 리스트와 오른쪽 리스트를 합칠때 오른쪽 리스트의 값을 추가할때 왼쪽 리스트에 남은 원소개수를 count한다.

코드

from sys import stdin

input = stdin.readline

#합치는 함수
def merge(arr, start, mid, end):
    global count
    left = start #왼쪽 리스트 시작 index
    right = mid+1 #오른쪽 리스트 시작 index
    r_index = start #arr의 실제 index
    
    while left<=mid and right<=end:
        if arr[left]<=arr[right]:#왼쪽 리스트가 가리키는 원소가 작다면
            result[r_index] = arr[left]
            left+=1
        else:#오른쪽 리스트에서 가리키는 원소가 작다면
            result[r_index] = arr[right]
            right+=1
            count += mid-left+1 #왼쪽 정렬의 남은 원소개수를 더한다.
        r_index+=1
    
    if left>mid: #오른쪽 리스트에 원소가 남아있다면 넣는다.
        for i in range(right,end+1):
            result[r_index] = arr[i]
            r_index+=1
    else: #왼쪽 리스트에 원소가 남아있다면 넣는다.
        for i in range(left,mid+1):
            result[r_index] = arr[i]
            r_index+=1

    #왼쪽 리스트와 오른쪽 리스트가 정렬된 result를 arr에 옮긴다.
    for i in range(start,end+1):
        arr[i] = result[i]

#쪼개는 함수
def mergesort(arr, start, end):
    if start<end:
        mid = (start+end)//2
        mergesort(arr,start, mid) #왼쪽으로 쪼갬
        mergesort(arr,mid+1, end) #오른쪽으로 쪼갬
        merge(arr,start,mid,end) #다 쪼갠 후 붙임

n = int(input())
arr = list(map(int,input().split()))
result = [0 for _ in range(n)]
count = 0

mergesort(arr,0,n-1) #배열, 인덱스 : 0~(n-1)까지의 

print(count)

다른 풀이(세그먼트 트리)

세그먼트 트리를 이용해서 푸는 방법도 있다. N개의 원소를 index와 묶어서 li에 저장한뒤 li를 원소기준으로 정렬시키고 나서 세그먼트 트리를 구하는 방식이다.

0. i : 0~n-1
1. li[i]의 원래 index부터 n-1까지의 세그먼트 트리 합을 s에 넣는다.
2. li[i]를 세그먼트 트리에 넣는다.
   위를 반복한다.

여기서 이용하는 개념은 i번째 수(n)을 기준으로 뒤에 n보다 작은 수가 몇개 있는지 세는 방법이다.

예시인 3 2 1 에서
3뒤에 3보다 작은수는 2, 1로 2개
2뒤에 2보다 작은수는 1로 1개
1뒤에 1보다 작은수는 0개이다.

여기서 가장 작은수부터 넣고, 작은수가 있던 위치 뒤로 수가 몇개가 있는지 파악하는 것이다.

그래서 세그먼트 트리에 1을 넣기 전에 1뒤에 있던 수를 sum으로 구한뒤 1을 넣어주고,2를 넣기 전에 2뒤에 있던 수(1)를 sum으로 구하는 방법을 사용한다.

3 / 3 2 1로 입력했을때 진행과정이다.

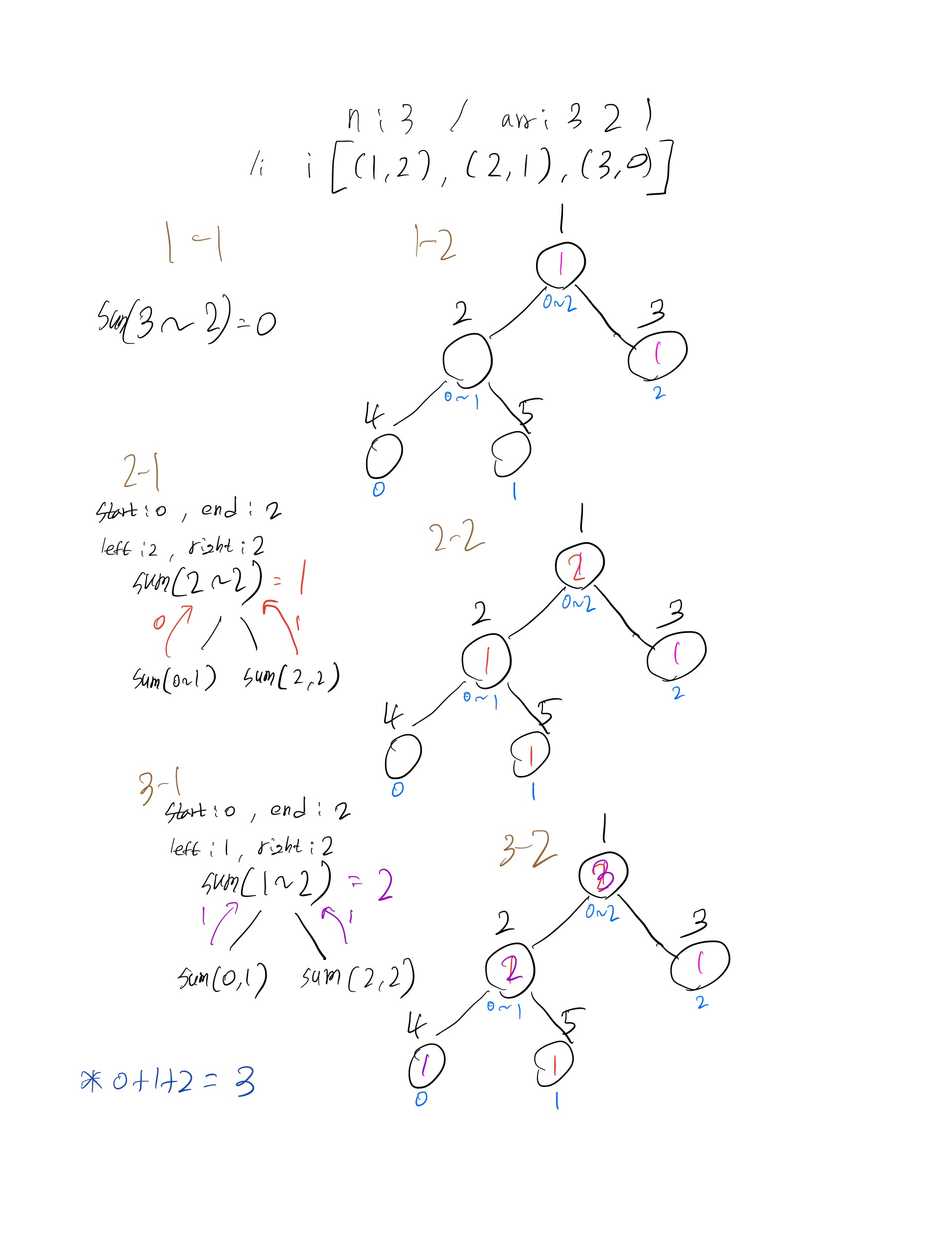
3 / 2 3 1로 입력했을때 진행 과정이다.

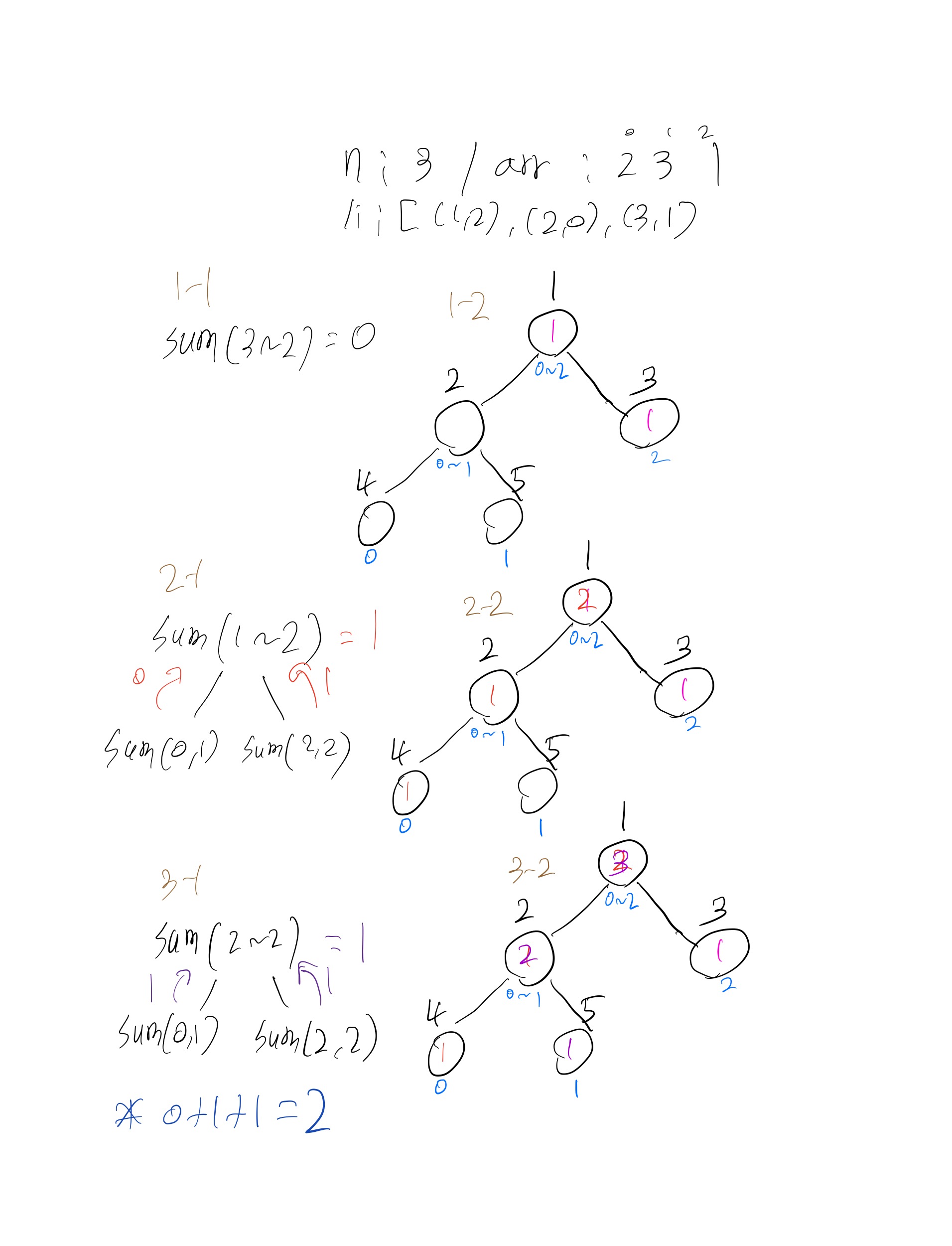
즉 나중에 넣는데(큰수), 먼저 넣은수(작은수)가 뒤에 있다면(인덱스가 크다면) 그걸 세는 것이다.

다른 코드(세그먼트 트리)

#PyPy3로 제출해야 함
from sys import stdin

input = stdin.readline

#start : li의 시작 인덱스(0), end : li의 끝 인덱스(n-1), node : 트리의 index
#index : li에서 바꾸고자 하는 인덱스, dif : li[index]의 변화하고자 하는 차이
def update(start, end, node, index, dif):
    if index<start or index>end:
        return 0
    
    tree[node] += dif

    if start==end:
        return 0
    
    mid = (start+end)//2
    update(start,mid,node*2,index,dif)
    update(mid+1,end,node*2+1, index, dif)

#start : li의 시작 인덱스(0), end : li의 끝 인덱스(n-1), node : 트리의 index
#left : li에서 구하고자 하는 구간 시작 인덱스, right : li에서 구하고자 하는 구간 끝 인덱스
def sum(start, end, node, left, right):
    if left>end or right<start:
        return 0
    if left<=start and end<=right:
        return tree[node]

    mid = (start+end)//2
    return sum(start,mid,node*2,left,right)+sum(mid+1,end,node*2+1,left,right)


n = int(input())
tree = [0 for _ in range(n*4)] #세그먼트 트리
arr = list(map(int,input().split()))
li = list()
s = 0 #연산횟수

#arr의 값을 (값,인덱스)형태로 묶어 li에 저장
for i in range(n):
    li.append((arr[i],i))

#li를 오름차순으로 저장
li.sort()

#가장 작은 수부터 트리에 넣으면서 값 뒤에 자기보다 작은수가 몇개인지 카운트
for i in range(n):
    s+= sum(0,n-1,1,li[i][1]+1,n-1)#li[i]의 인덱스보다 뒤에있는 값중에 작은 값들을 count
    update(0,n-1,1,li[i][1],1)#li의 값을 헤당 인덱스에 맞게 tree에 저장

print(s)

참고

병합정렬 풀이
세그먼트 트리 풀이
세그먼트 트리 풀이2