문제
https://www.acmicpc.net/problem/2004
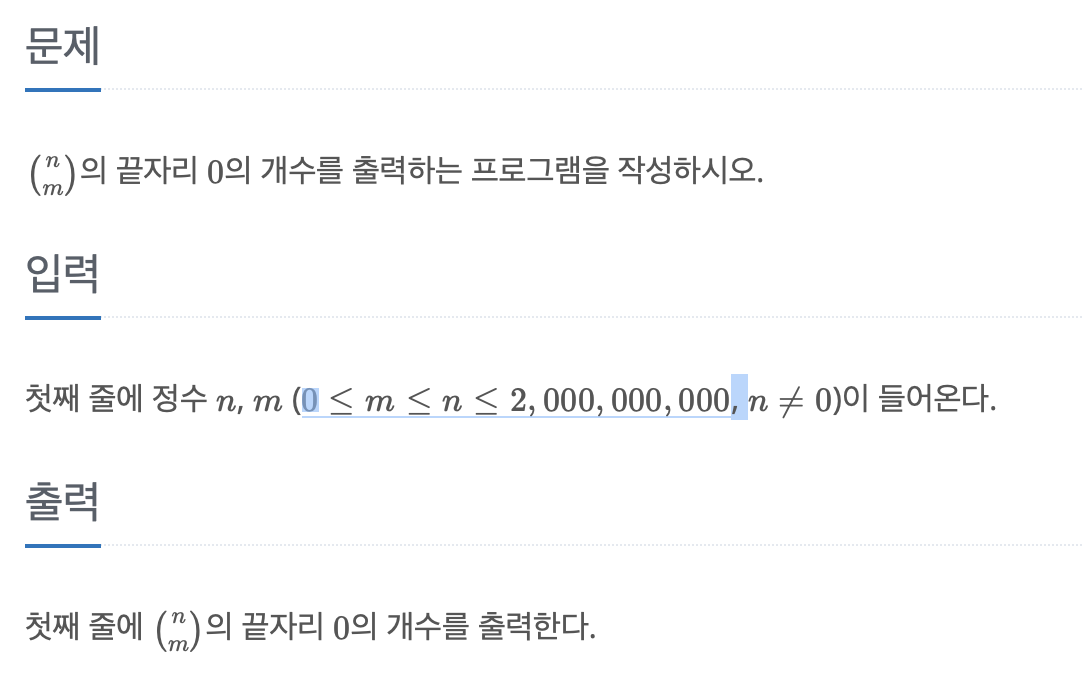
풀이
팩토리얼을 사용해서 을 구한뒤 10으로 나누는 방식으로 정답을 구하려고 하면 너무 큰 n,m조건때문에 시간초과가 날 수 있다.
0의 개수는 2와 5의 쌍의 개수라고 할 수 있다. 즉, 에서 2와 5의 개수를 구한 뒤 작은 개수가 0의 개수가 될 것이다.
코드
from sys import stdin
input = stdin.readline
#n!에 있는 2의 개수를 새는 방법
def two_count(n):
count = 0
while n!=0:
n //=2
count += n
return count
#n!에 있는 5의 개수를 세는 방법
def five_count(n):
count = 0
while n!= 0:
n//=5
count += n
return count
n, m = map(int, input().split())
# 빼는 이유는 조합을 구하는 식이 n!/r! * (n-r)!인데, 조합의 2의 개수는 n!의 2의 개수에다가 r!과 (n-r)!의 2의 개수를 뺀 것이다.
# min을 쓰는 이유는 뒷자리가 0이려면 2 와 5의 쌍의 개수이기 때문에 둘 중 작은 것이 쌍의 개수이다.
print(min(two_count(n)-two_count(n-m)-two_count(m),five_count(n)-five_count(n-m) -five_count(m)))추가 설명
def two_count(n):
count = 0
while n!=0:
n //=2
count += n
return count이 코드가 이해가 안갈 수 있다.
예를 들어 n이 8 이라면
에서의 2의 개수는
이렇게 7개 이다. 위 코드는 이를 더한 식이다.
8에서 의 개수 : 4
8에서 의 개수 : 2
8에서 의 개수 : 1
이렇게 count는 4+2+1 로 값이 더해진다.
