문제 설명

첫 번째 분수의 분자와 분모를 뜻하는 numer1, denom1, 두 번째 분수의 분자와 분모를 뜻하는 numer2, denom2가 매개변수로 주어집니다. 두 분수를 더한 값을 기약 분수로 나타냈을 때 분자와 분모를 순서대로 담은 배열을 return 하도록 solution 함수를 완성해보세요.

class Solution {
    public int[] solution(int numer1, int denom1, int numer2, int denom2) {
        int[] answer = {};
        return answer;
    }
}

제한 사항

• 0 <numer1, denom1, numer2, denom2 < 1,000

입출력 예

입출력 예 설명

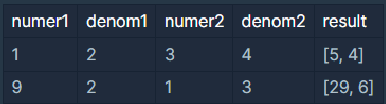
• 입출력 예 #1

  • 1 / 2 + 3 / 4 = 5 / 4입니다. 따라서 [5, 4]를 return 합니다.

• 입출력 예 #2

  • 9 / 2 + 1 / 3 = 29 / 6입니다. 따라서 [29, 6]을 return 합니다.

---

해결법

방법 1

class Solution {
    public int[] solution(int numer1, int denom1, int numer2, int denom2) {
    
        int numerator = (numer1 * denom2) + (numer2 * denom1);		// A * D + B * C
        int denominator = denom1 * denom2;		// B * D
        
        for(int i = numerator-1; i > 1; i--) {
            // 기약분수로 만들기
            if(numerator % i == 0 && denominator % i == 0) { 
                numerator /= i;
                denominator /= i;
            }
        }
        
        int[] answer = {numerator, denominator};
        return answer;
    }
}

• 분수 계산법
  

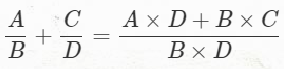
• for 반복문

  • A D + B C 에서 분자가 분모보다 클 수 밖에 없으므로, i 의 초기값은 numerator-1
  • 음수나 0으로 나눌 수는 없으므로, i > 1
  • 점점 수를 줄여가며 반복할 것이므로, i--

• {numerator, denominator} : answer 배열에 계산된 분자와 분모를 담기 위해

방법 2

class Solution {
    public int[] solution(int numer1, int denom1, int numer2, int denom2) {
    
        int[] answer = {numer1, denom1, numer2, denom2};
        
        int numerator = (numer1 * denom2) + (numer2 * denom1);
		int denominator = denom1 * denom2;
        
        int divisor = gcd(numerator, denominator);
            numerator /= divisor;
            denominator /= divisor;

        int[] result = {numerator, denominator};

        return result;
    }

    // 유클리드 호제법
    public int gcd(int a, int b){
        // a가 b보다 크다면 실행.
        if (a <= b){
            int temp = a;
            a = b;
            b = temp;
        }
        if(b == 0){
            return a;
        }
        return gcd(b, a % b);
    }
}

• 유클리드 호제법을 이용해서 풀 수도 있다.

참고: 유클리드 호제

---

분수의 덧셈