메모

/*
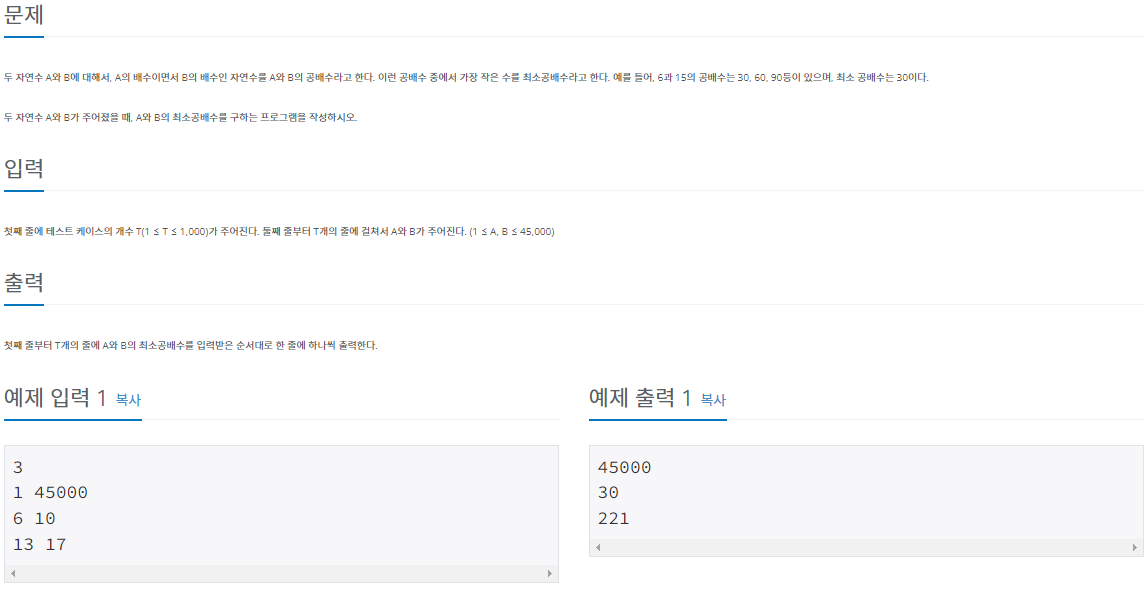
자연수 A (1 ≤ A ≤ 45,000)
자연수 B (1 ≤ B ≤ 45,000)
최소공배수 = A의 배수이면서 B의 배수인 자연수 중 최소값

A와 B의 최소공배수를 구하기?
*/

---

해결법

방법 1

/**
     * 유클리드 호제법 구현 메서드
     * @param bn : 큰 숫자
     * @param sn : 작은 숫자
     * @return
     * 큰 숫자를 작은숫자로 나눈 값이 0이면 작은숫자 리턴, 아니면 재귀형태로 자신을 호출
     */
     
    public int eucd(int A, int B) {
        // 큰숫자를 작은숫자로 나눈 나머지를 계산
        int r = bn % sn;
        // 나머지가 0이면 작은숫자가 최대공약수이므로 작은숫자 리턴
        if (r == 0) {
            return sn;
        } else {
            // 나머지가 0 이상이면 재귀형태로 호출
            // 이때 파라미터는 작은숫자와 나머지를 넣어줌
            return eucd(sn, r);
        }
    }
    
import java.util.Scanner;
 
public class Main {
	public static void main(String[] args) {
		
		Scanner in = new Scanner(System.in);
		
		int N = in.nextInt();
        
		StringBuilder sb = new StringBuilder();
 
		for (int i = 0; i < N; i++) {
			
			int a = in.nextInt();
			int b = in.nextInt();
			
			int d = gcd(a, b);		// gcd() 메소드 실행결과를 변수 d 에 입력 -> d : 최대 공약수
			
			sb.append(a * b / d).append('\n');		// 최소 공배수
		}
        
		System.out.println(sb);
	}
    
	// 최대 공약수 반복문
	public static int gcd(int a, int b) {
 
		while (b != 0) {
			int r = a % b;		// r : 나머지
 
			// GCD(a, b) = GCD(b, r)이므로 변환한다. (즉, GCD(b, a % b))
			a = b;
			b = r;
		}
        
		return a;		// 최대 공약수
	}
}    

• 참고: 유클리드 호제법

---

참고: [백준] 1934번 : 최소공배수 - JAVA [자바]

---

최소공배수 (백준 1934번)