⭐실력진단 결과

깊이우선탐색을 어떤 문제에 어떻게 적용하는지에 대해서 배우게 됩니다.
기본개념
🟢그래프 탐색
✏️DFS, 깊이 우선 탐색
-
특정 정점(노드)에서 시작하여 갈 수 있는 곳까지 쭉 따라 들어갔다가 더 이상 갈 곳이 없으면 빠져나오는 방식의 그래프 탐색 방법
-
재귀함수 이용
✏️그래프 상에서의 DFS 탐색
- : 정점(노드)의 수, : 간선의 수
- 인접 행렬 - 공간 복잡도 :
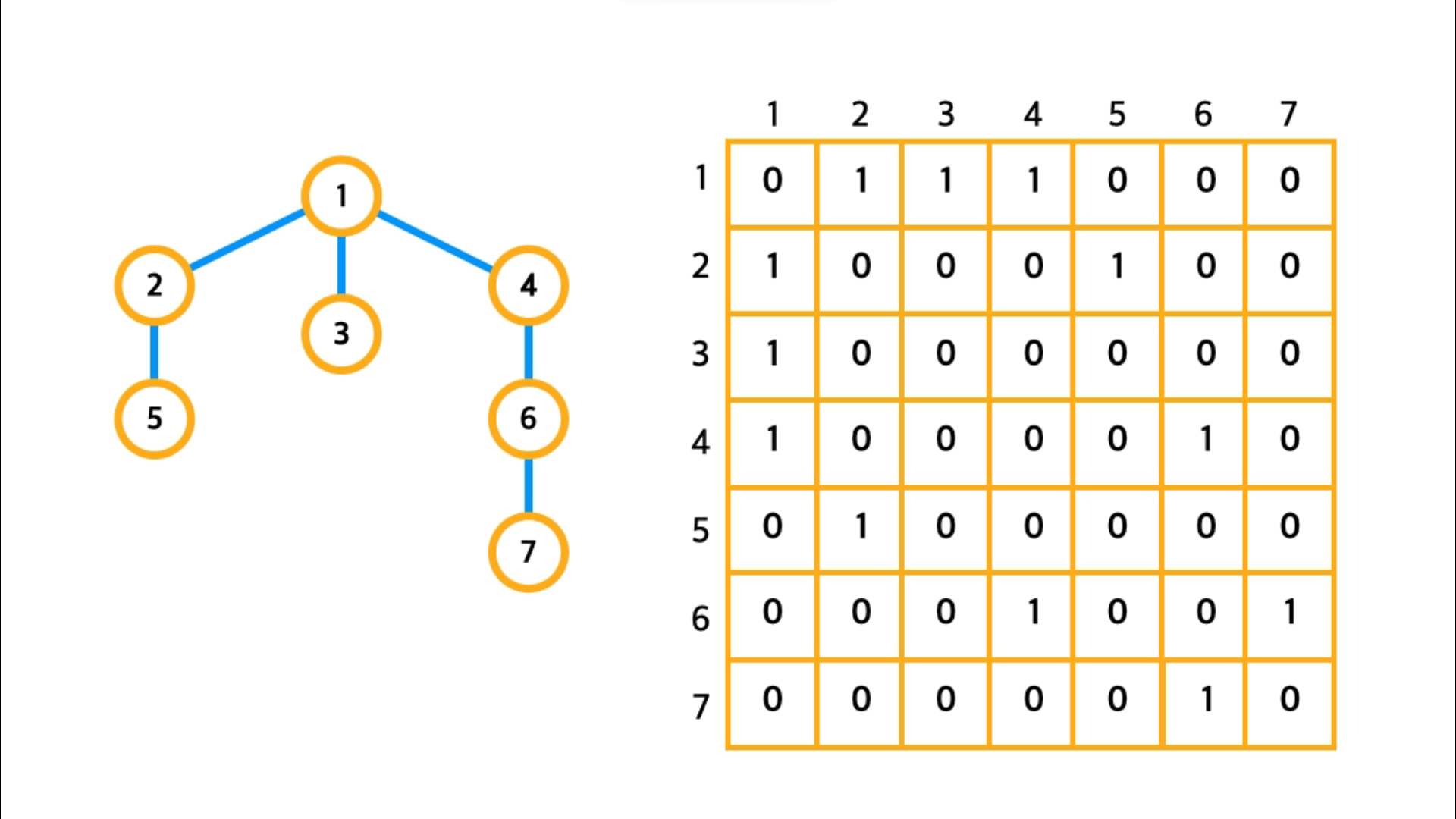
- 인접 리스트 - 공간 복잡도 :
개의 동적 배열, 각 간선( )별로 정점이 2개씩 동적 배열에 각각 추가
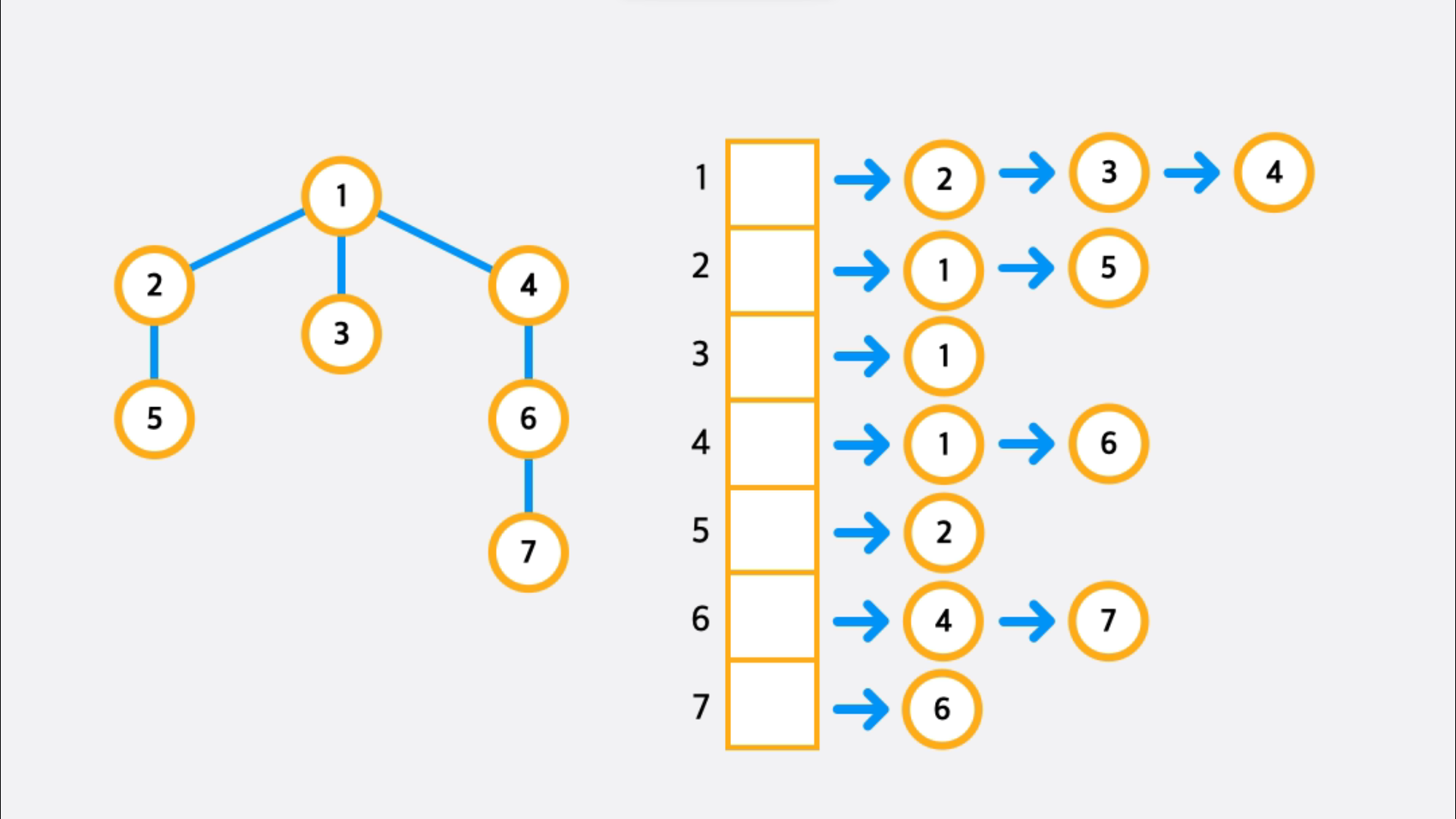
✏️그래프 탐색 알고리즘의 대원칙
- 시작점으로부터 연결된 모든 정점을 전부 방문해야 한다.
- 이미 방문한 정점은 다시 방문하지 않는다.
⇒ 정점의 개수만큼의 크기를 갖는 visited 리스트를 만들어 방문한 위치와 방문하지 않은 위치 저장해야 한다.
DFS 함수를 호출하기 전에 해당 위치의 visited 값을 True로 변경한다.
📌문제
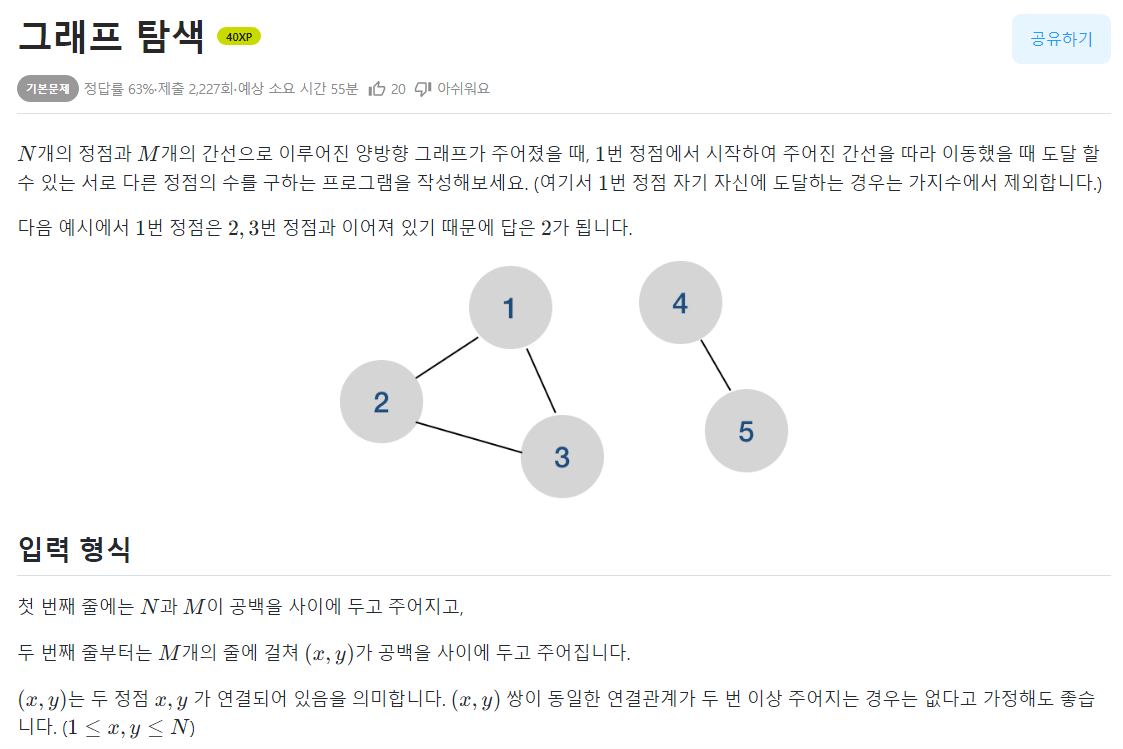
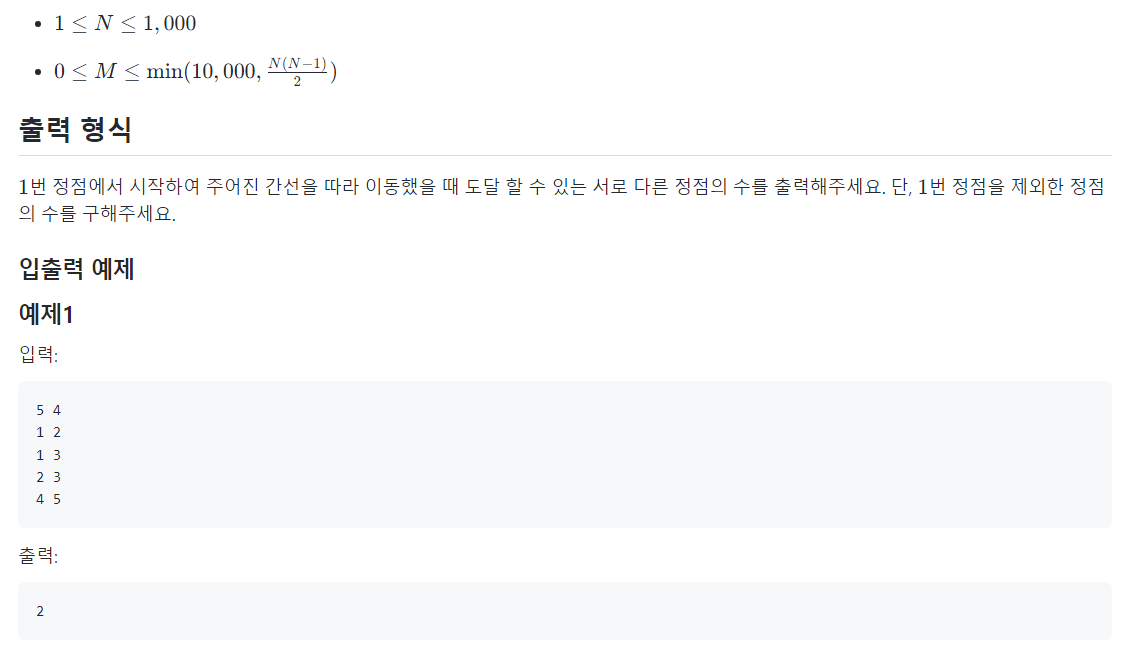

📌나의 코드
# 노드 수, 간선 수
n, m = map(int, input().split())
# 인접 리스트
graph = [[] for _ in range(n + 1)]
for _ in range(m):
x, y = map(int, input().split())
# 양방향이므로 서로 넣어준다.
graph[x].append(y)
graph[y].append(x)
# 방문 리스트
visited = [False for _ in range(n + 1)]
def dfs(v):
global cnt
for i in graph[v]:
if not visited[i]:
# 1번 정점은 제외
if i != 1:
cnt += 1
visited[i] = True
dfs(i)
cnt = 0
dfs(1)
print(cnt)✏️개선점
처음에 1번 정점을 방문했다고 저장하면 정점마다 1번인지 아닌지 확인하지 않아도 된다.
🟢두 방향 탈출 가능 여부 판별하기
✏️그리드 상에서의 DFS 탐색
- 일반적인 그래프에서 두 정점의 연결관계 표현 = 인접 행렬 또는 인접 리스트
- 2차원 격자에서는 일반적으로 인접한 곳으로만 이동이 가능하므로, 인접 행렬이나 인접 리스트를 만들 필요가 없다.
그래프에서의 DFS 탐색
- 재귀함수 필요
- 인자로 현재 위치를 나타내는 vertex 값 필요
격자에서의 DFS 탐색
- 현재 위치 표현을 위해 행렬에서의 x행 y열을 의미하는 (x, y) 2개의 값이 반드시 필요
⇒ visited 배열 역시 2차원이 되어야 함, 0번지부터 사용하면 시작 위치가 (0, 0)
DFS 함수에서는 현재 위치 (x, y)로부터 갈 수 있는 곳들을 전부 탐색, 갈 수 있다면 해당 위치를 방문 처리한 뒤 재귀함수 다시 호출
- 그리드 문제에서는 인접한 칸들로만 이동 가능, dx, dy 테크닉을 이용하여 new_x, new_y에 인접한 칸의 위치가 오도록 설정
visited 방문 표시 위치
- visted 배열 방문 표시 위치를 재귀 함수 호출 전이 아닌 재귀 함수 진입 순간에 진행하는 것도 가능
- 하지만, BFS 탐색에서는 반드시 queue에 넣기 전에 visited 배열에 방문 표시를 야 하기 때문에, 가능하면 DFS 탐색에서도 재귀 함수 호출 직전에 visited 표기를 하는 패턴으로 연습
📌문제
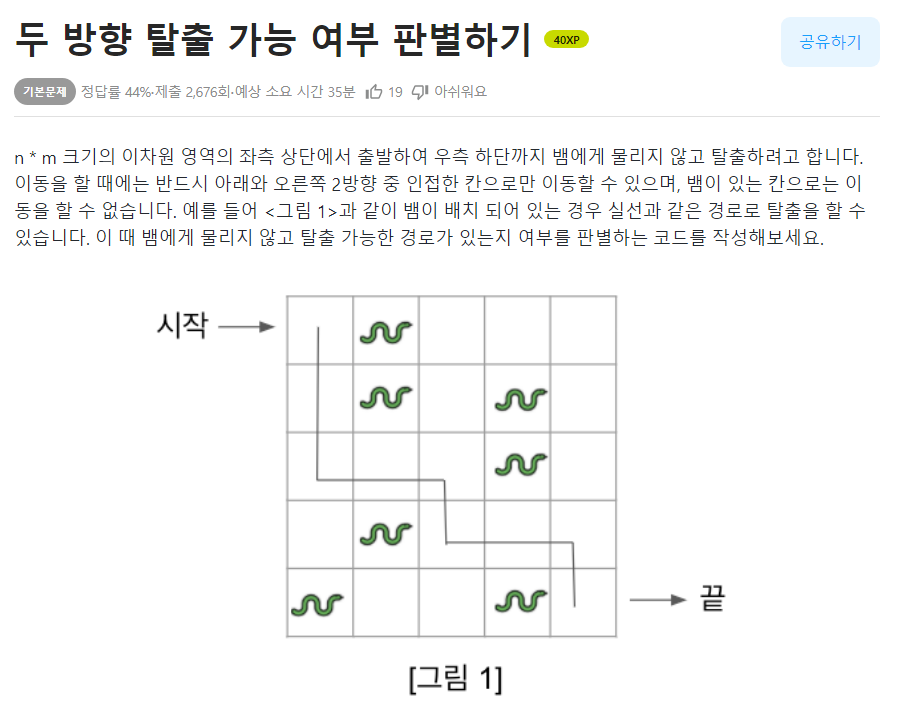
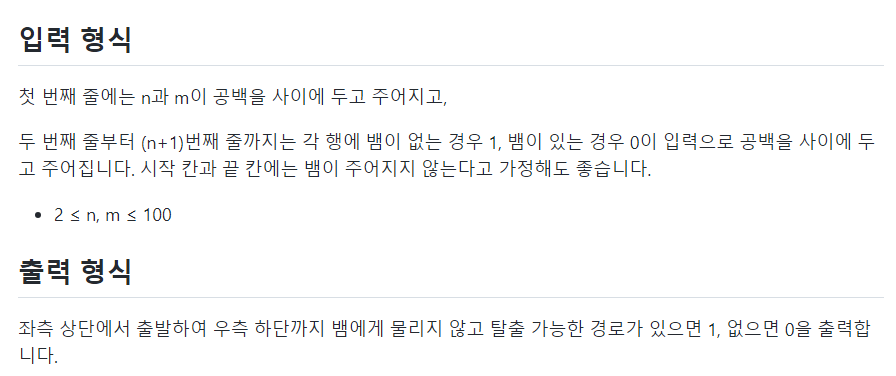


📌나의 코드
n, m = map(int, input().split())
grid = [list(map(int, input().split())) for _ in range(n)]
visited = [[0] * m for _ in range(n)]
def in_range(x, y):
return 0 <= x and x < n and 0 <= y and y < m
# 갈 수 있는 좌표인지 확인
def can_go(x, y):
# 다음 좌표가 격자 안에 있는지 확인
if not in_range(x, y):
return False
# 이미 방문했거나 뱀이 있는지 확인
if visited[x][y] or grid[x][y] == 0:
return False
return True
def dfs(x, y):
# 아래, 오른쪽
dxs, dys = [1, 0], [0, 1]
for dx, dy in zip(dxs, dys):
# 다음 좌표
new_x, new_y = x + dx, y + dy
# 갈 수 있는 곳이면 방문 처리 후 재귀함수 실행
if can_go(new_x, new_y):
visited[new_x][new_y] = 1
dfs(new_x, new_y)
dfs(0, 0)
# 끝지점 방문했다면 1 출력, 아니면 0 출력
if visited[n - 1][m - 1]:
print(1)
else:
print(0)✏️개선점
- 답은 맞았지만, 처음 위치 방문 처리하지 않았다.
dfs 실행 전에visited[0][0] = 1추가해야 한다. - visited 배열에서 방문했으면 1, 아니면 0이므로 결과적으로 visited의 끝 점을 출력하면 된다.
연습문제
🟠마을 구분하기
📌문제

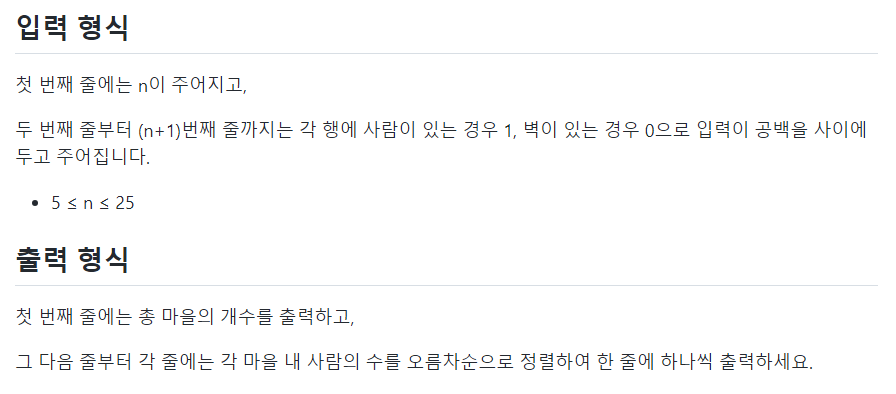

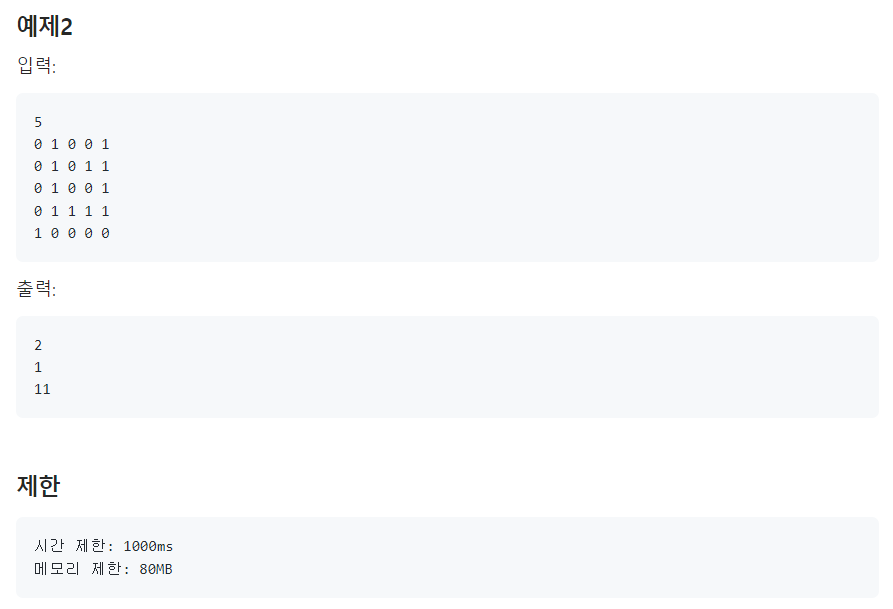
📌나의 코드
n = int(input())
people = [list(map(int, input().split())) for _ in range(n)]
visited = [[0] * n for _ in range(n)]
# 마을 내 사람 수
cnt = 0
# 사람 수 리스트
residents = []
def in_range(x, y):
return 0 <= x and x < n and 0 <= y and y < n
def can_go(x, y):
if not in_range(x, y):
return False
if visited[x][y] or people[x][y] == 0:
return False
return True
def dfs(x, y):
global cnt
# 상, 하, 좌, 우
dxs, dys = [-1, 1, 0, 0], [0, 0, -1, 1]
for dx, dy in zip(dxs, dys):
nx, ny = x + dx, y + dy
if can_go(nx, ny):
visited[nx][ny] = 1
cnt += 1
dfs(nx, ny)
for i in range(n):
for j in range(n):
# 위치를 방문할 수 있다면
if can_go(i, j):
# 방문 여부 갱신
visited[i][j] = 1
# 새로운 마을 탐색한다는 의미로 cnt를 1로 갱신
cnt = 1
dfs(i, j)
# 한 마을 탐색 후 마을 내 사람 수 저장
residents.append(cnt)
# 마을 수 = 각 마을 내 사람 수 리스트 길이
print(len(residents))
# 각 마을 내 사람 수 오름차순 정렬
residents.sort()
for r in residents:
print(r)🔓풀이
마을과 같이 연결되어 있는 부분을 여러 개 찾을 때는 반복문을 사용하여 탐색을 여러 번 시행해준다.
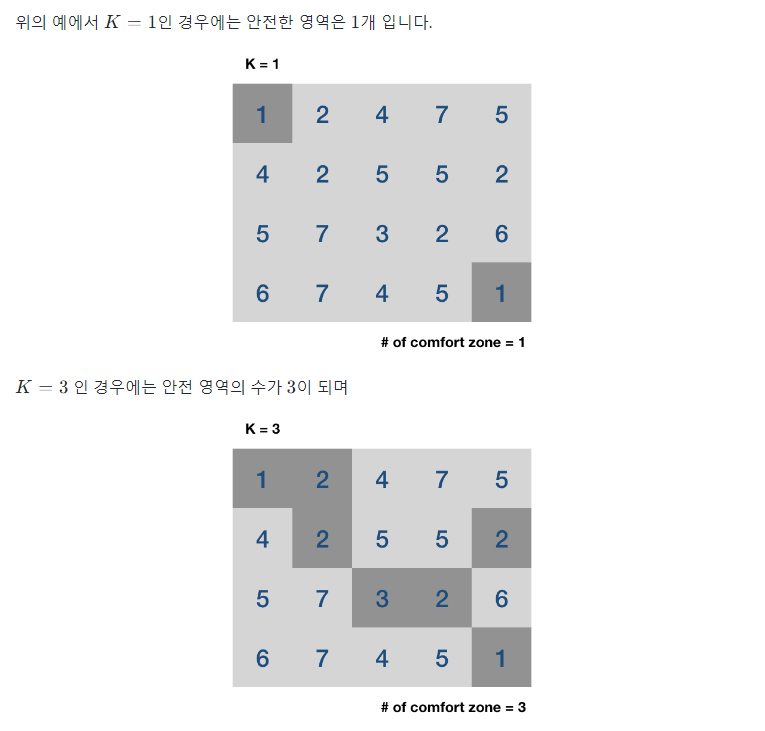
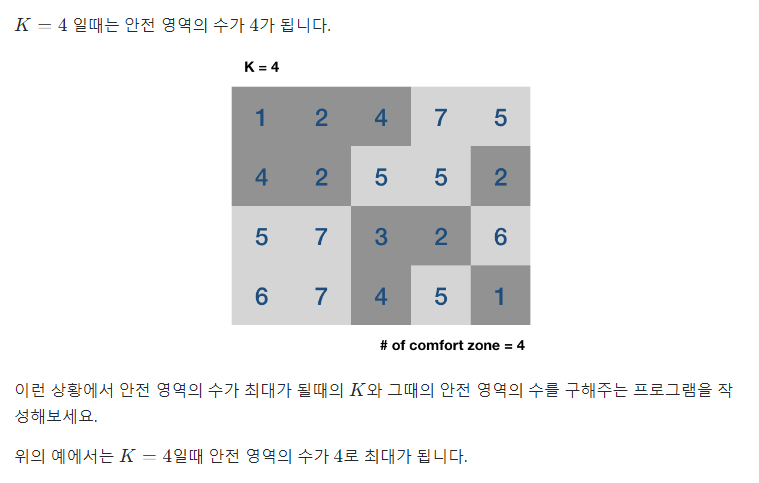
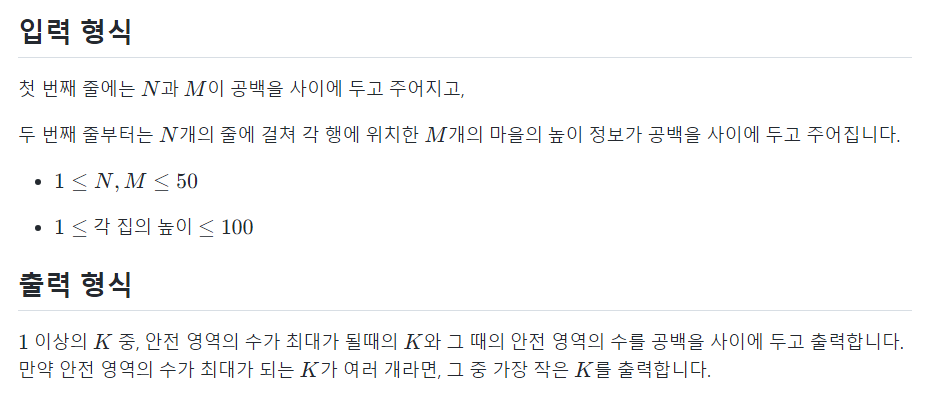
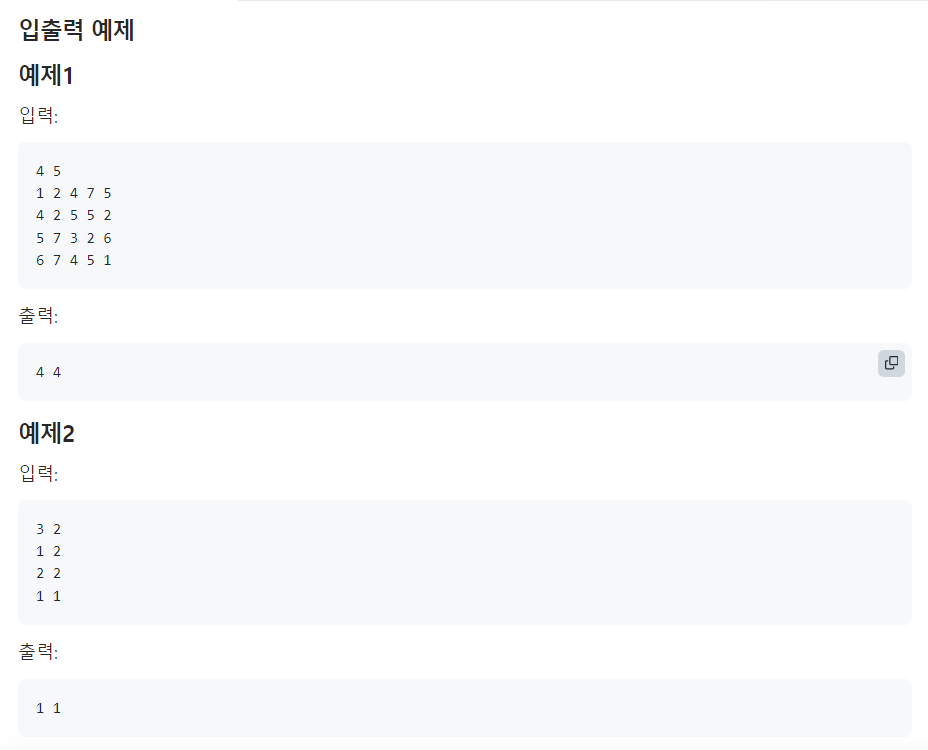
❌🟠안전 지대
📌문제

📌나의 코드
import sys
sys.setrecursionlimit(2500)
n, m = map(int, input().split())
houses = [list(map(int, input().split())) for _ in range(n)]
# k의 최댓값 = 집 높이의 최댓값
max_k = max(max(houses))
def in_range(x, y):
return 0 <= x and x < n and 0 <= y and y < m
def can_go(x, y, k):
# 격자를 벗어나면 False
if not in_range(x, y):
return False
# 집 높이가 k보다 작거나 같으면 또는 이미 방문한 위치면 False
if houses[x][y] <= k or visited[x][y]:
return False
return True
def dfs(x, y, k):
# 상, 하, 좌, 우
dxs, dys = [-1, 1, 0, 0], [0, 0, -1, 1]
for dx, dy in zip(dxs, dys):
nx, ny = x + dx, y + dy
if can_go(nx, ny, k):
visited[nx][ny] = 1
dfs(nx, ny, k)
max_area = 0
ans_k = 1
for k in range(1, max_k + 1):
num_of_area = 0
visited = [[0] * m for _ in range(n)]
for i in range(n):
for j in range(m):
# 갈 수 있는 좌표면 방문 표시
if can_go(i, j, k):
visited[i][j] = 1
num_of_area += 1
dfs(i, j, k)
# 현재 최대 영역의 수보다 큰 경우 갱신
if max_area < num_of_area:
max_area, ans_k = num_of_area, k
print(ans_k, max_area)✏️오답노트
재귀함수가 너무 깊게 들어가면 Error가 발생하므로 최대로 들어갈 깊이를 계산하여 sys.setrecursionlimit(최대로 들어갈 깊이) 을 설정해주어야 한다.
테스트
🟠뿌요뿌요
📌문제
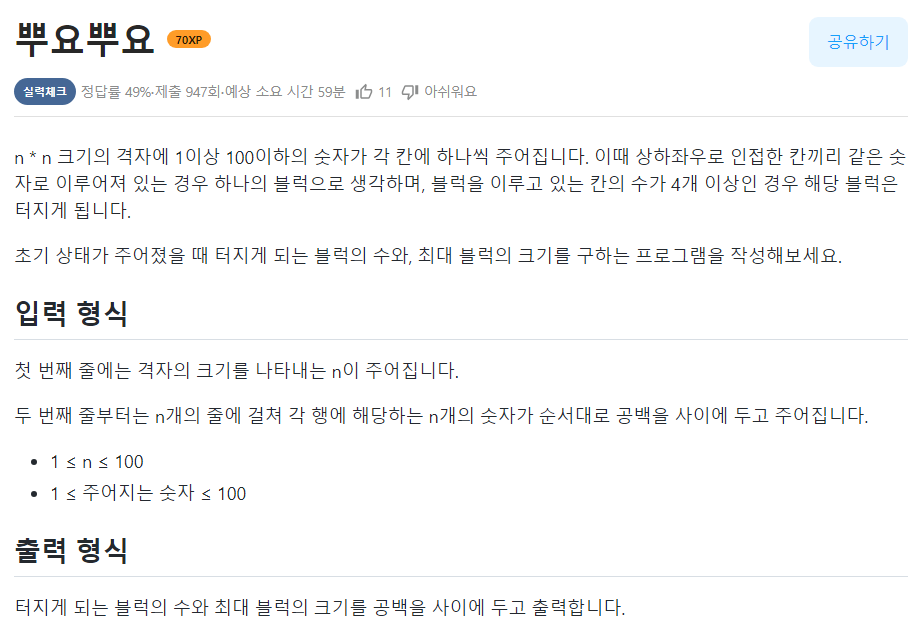
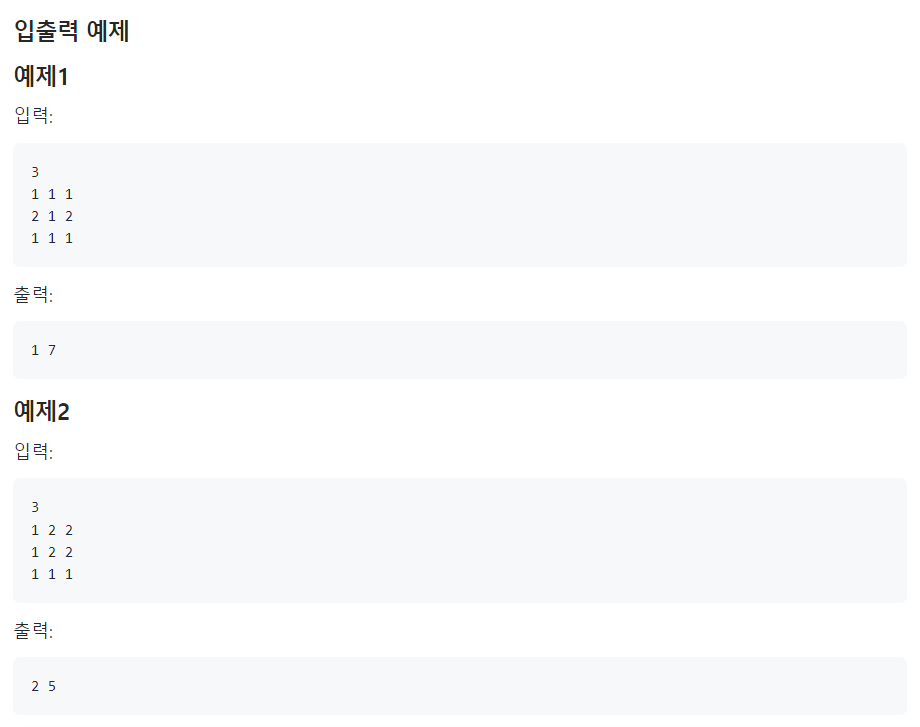

📌나의 코드
n = int(input())
grid = [list(map(int, input().split())) for _ in range(n)]
visited = [[0] * n for _ in range(n)]
# 격자 벗어나는지 확인
def in_range(x, y):
return 0 <= x and x < n and 0 <= y and y < n
# 갈 수 있는 위치인지 확인
def can_go(x, y):
if not in_range(x, y):
return False
if visited[x][y]:
return False
return True
def dfs(x, y):
global block_cnt
# 상, 하, 좌, 우
dxs, dys = [-1, 1, 0, 0], [0, 0, -1, 1]
for dx, dy in zip(dxs, dys):
nx, ny = x + dx, y + dy
# 갈 수 있는 위치이고, 다음 숫자가 같은 숫자인 경우 방문
if can_go(nx, ny) and grid[nx][ny] == grid[x][y]:
visited[nx][ny] = 1
block_cnt += 1
dfs(nx, ny)
boom = 0
max_block_cnt = 0
for i in range(n):
for j in range(n):
# 새로운 블럭 탐색
block_cnt = 1
if can_go(i, j):
visited[i][j] = 1
dfs(i, j)
# 블럭의 수가 4개 이상인 경우 터지는 블럭 수 1 증가
if block_cnt >= 4:
boom += 1
# 현재 블럭의 수가 기존의 최대 블럭의 수보다 클 경우 갱신
if max_block_cnt < block_cnt:
max_block_cnt = block_cnt
print(boom, max_block_cnt)
