⭐실력진단 결과

dx, dy 테크닉을 이용해 격자에서의 이동을 간결하게 구현하는 방법을 배우게 됩니다.

❌🔴거울에 레이저 쏘기 2

📌문제

📌나의 코드

🤔

---

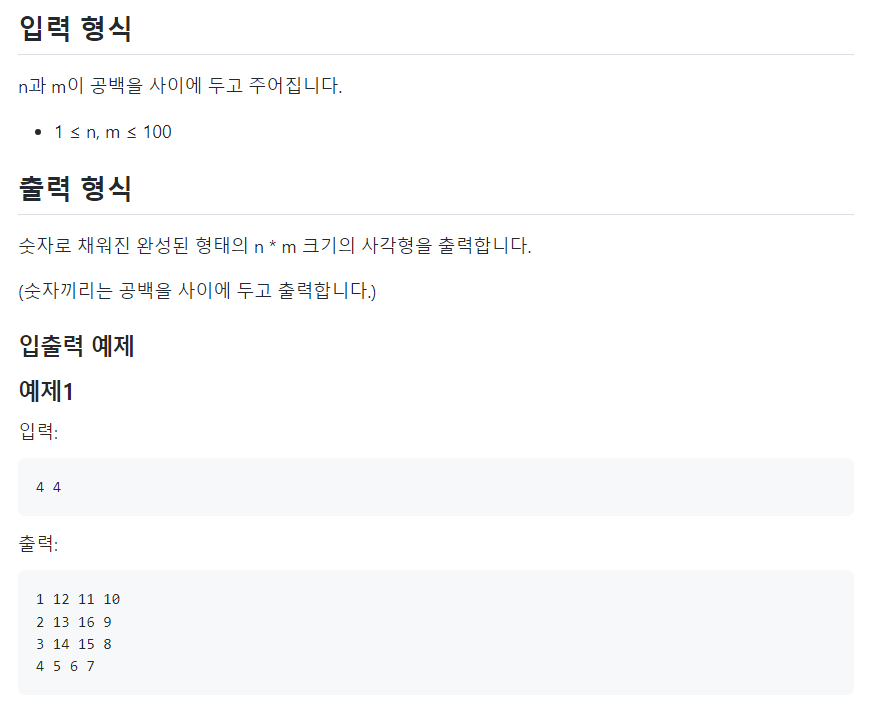
🔴빙빙 돌며 숫자 사각형 채우기 2

📌문제

📌나의 코드

Runtime: 89ms, Memory: 30MB

# 행 길이, 열 길이
n, m = map(int, input().split())

# 시작 위치
x, y = 0, 0
grid = [[0] * m for _ in range(n)]

# (0, 0)에서 1부터 시작
grid[x][y] = 1

# 아래, 오른쪽, 위, 왼쪽
dxs, dys = [1, 0, -1, 0], [0, 1, 0, -1] 
dir_num = 0

# 격자에서 벗어났는지 확인
def in_range(x, y):
    return 0 <= x and x < n and 0 <= y and y < m

for i in range(2, n * m + 1):
    # 다음 위치 계산
    x, y = x + dxs[dir_num], y + dys[dir_num]
    
    # 범위를 벗어났거나 이미 값이 있는 경우
    if not in_range(x, y) or grid[x][y] != 0:
        # 이전 위치로 돌아왔다가
        x, y = x - dxs[dir_num], y - dys[dir_num]
        # 방향을 바꿔주고
        dir_num = (dir_num + 1) % 4
        # 다시 다음 위치 계산
        x, y = x + dxs[dir_num], y + dys[dir_num]
    
    # 값은 2부터 격자 크기까지
    grid[x][y] = i

# 출력
for i in range(n):
    for j in range(m):
        print(grid[i][j], end=' ')
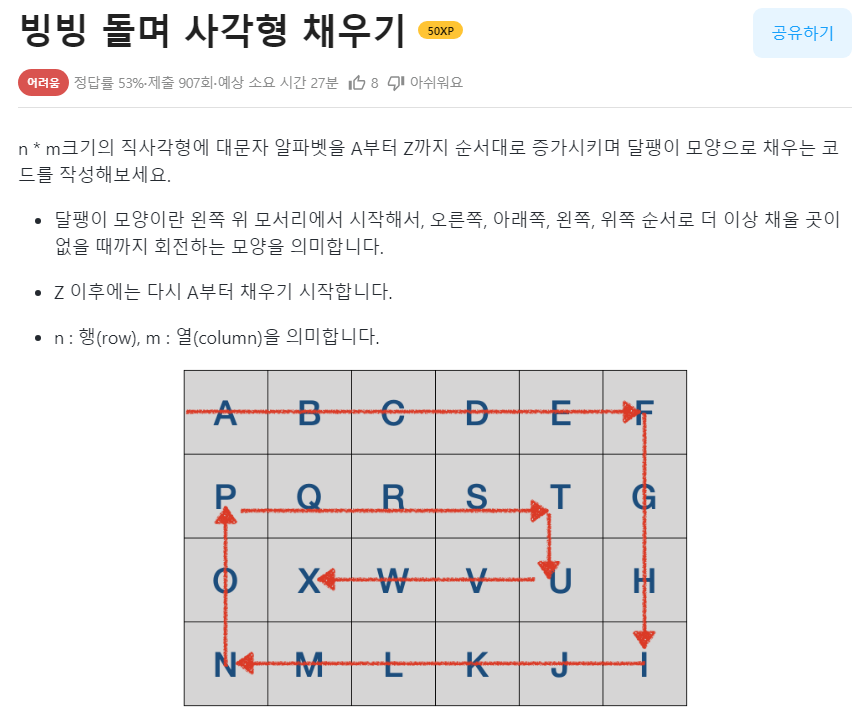
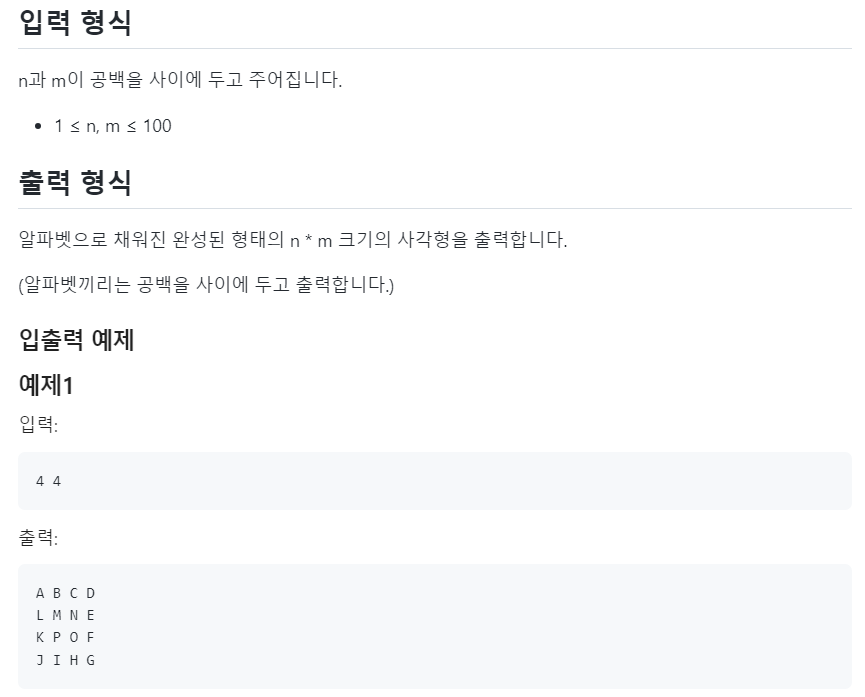
    print()

---

🔴빙빙 돌며 사각형 채우기

📌문제

📌나의 코드

Runtime: 92ms, Memory: 31MB

n, m = map(int, input().split())
grid = [[0] * m for _ in range(n)]

# 오른쪽, 아래쪽, 왼쪽, 위쪽
dxs, dys = [0, 1, 0, -1], [1, 0, -1, 0]
dir_num = 0  # 오른쪽 시작

# 시작 위치
x, y = 0, 0
grid[x][y] = 'A'
now = ord('A')

# 범위 확인
def in_range(x, y):
    return 0 <= x and x < n and 0 <= y and y < m

for _ in range(1, n * m):
    # 가능할 때까지 확인
    while True:
        # 현재 방향으로 다음 위치 계산
        nx, ny = x + dxs[dir_num], y + dys[dir_num]

        # 나아갈 수 있으면
        if in_range(nx, ny) and grid[nx][ny] == 0:
            # 위치 갱신
            x, y = nx, ny

            # 현재 알파벳이 Z 이전이면
            if now < ord('Z'):
                # 다음 알파벳으로
                now += 1
            # Z 이후이면
            else:
                # A로 돌아간다
                now = ord('A')

            grid[x][y] = chr(now)
            break
        
        # 나아갈 수 없다면
        else:
            # 시계방향 90` 회전
            dir_num = (dir_num + 1) % 4

for i in range(n):
    for j in range(m):
        print(grid[i][j], end=' ')
    print()

✏️ord(), chr() 함수

• ord() : 문자 → 유니코드 정수
• chr() : 정수 → 유니코드 문자

✏️개선점

for문 변수 i를 사용하면 Z에서 A로 돌아오는 알고리즘을 간단하게 작성할 수 있다.
알파벳(A ~ Z)은 총 26개
ord('A') = 65
ord('B') = 66 = 1 + ord('A') = (1 % 26) + ord('A')
ord('Z') = 90 = 25 + ord('A') = (25 % 26) + ord('A')

for i in range(1, n * m):
...
	...
    grid[x][y] = chr((i % 26) + ord('A'))
    ...
...

---

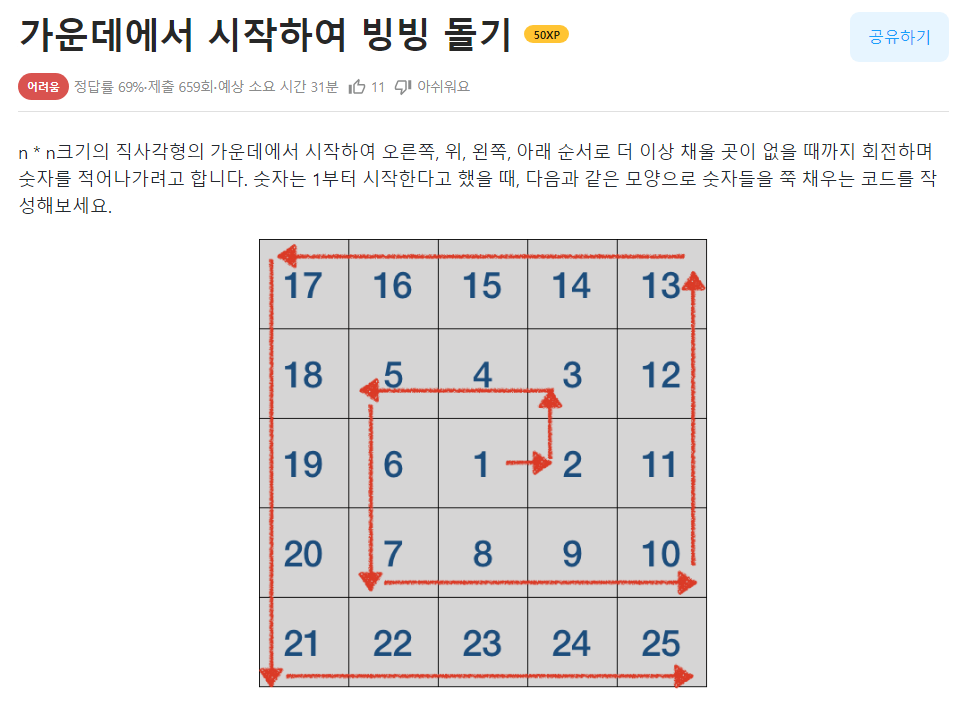
🔴가운데에서 시작하여 빙빙 돌기

📌문제

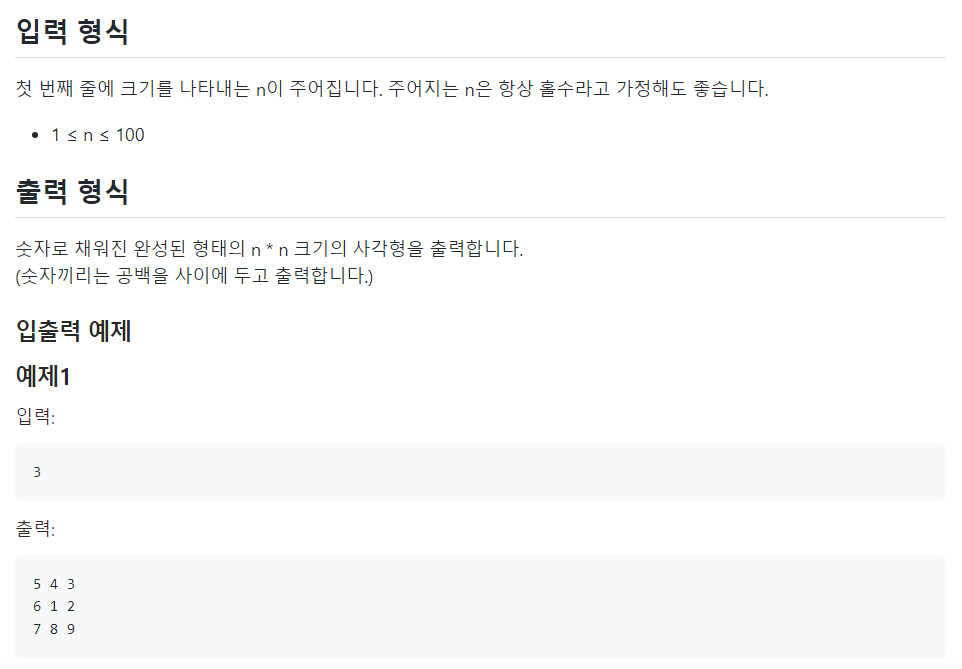
📌나의 코드

n = int(input())
grid = [[0] * n for _ in range(n)]

# 거꾸로 돌리기
# 왼쪽, 위, 오른쪽, 아래
dxs, dys = [0, -1, 0, 1], [-1, 0, 1, 0]
dir_num = 0

# 오른쪽 아래부터 시작
x, y = n - 1, n - 1
grid[x][y] = n * n

# 범위 확인
def in_range(x, y):
    return 0 <= x and x < n and 0 <= y and y < n

for i in range(n * n - 1, 0, -1):
    # 다음 위치 확인
    nx, ny = x + dxs[dir_num], y + dys[dir_num]
    
    # 나아갈 수 없으면 시계방향 90' 회전
    if not in_range(nx, ny) or grid[nx][ny] != 0:
        dir_num = (dir_num + 1) % 4
     
    # 나아갈 수 있으면 위치 갱신 및 값 저장
    x, y = x + dxs[dir_num], y + dys[dir_num]
    grid[x][y] = i 


for i in range(n):
    for j in range(n):
        print(grid[i][j], end=' ')
    print()

🔓풀이

문제 의도와는 다르지만, 가운데부터 시작하는 방법은 모르겠어서 끝나는 지점부터 가운데로 돌아오도록 작성

문제 의도에 맞게 푸는 경우
1. 이동 횟수에 대한 변수 추가
2. 이동 방향이 왼쪽이나 오른쪽일 때 이동 횟수 1 증가
3. 격자를 벗어나는지 확인하는 함수 추가

---

---

✔️테스트

🟠이동경로상에 있는 모든 숫자 더하기

📌문제

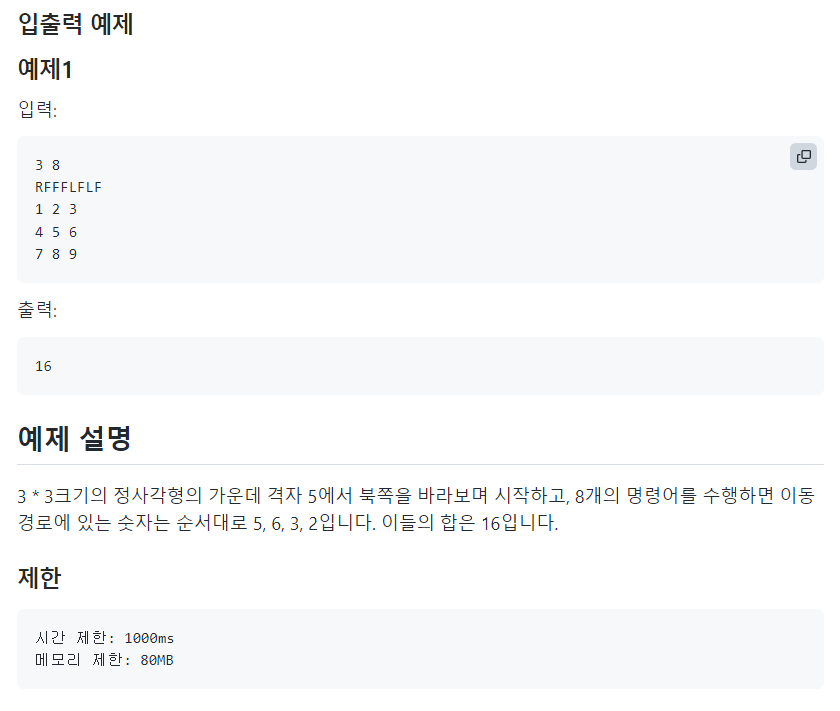
📌나의 코드

n, t = map(int, input().split())
s = input()
nums = [list(map(int, input().split())) for _ in range(n)]

# 북, 동, 남, 서
dxs, dys = [-1, 0, 1, 0], [0, 1, 0, -1]

# 가운데 위치에서 북쪽으로 시작
x, y = n // 2, n // 2
dir_num = 0

# 범위 확인
def in_range(x, y):
    return 0 <= x and x < n and 0 <= y and y < n

# 가운데 위치 값부터 합
ans = nums[x][y]

for i in s:
    # 왼쪽으로 90' 방향 전환
    if i == 'L':
        dir_num = (dir_num - 1 + 4) % 4
    # 오른쪽으로 90' 방향 전환
    elif i == 'R':
        dir_num = (dir_num + 1) % 4
    else:
        # 다음 위치 계산
        nx, ny = x + dxs[dir_num], y + dys[dir_num]
        # 범위 안에 있으면 합
        if in_range(nx, ny):
            x, y = nx, ny
            ans += nums[x][y]
    
print(ans)