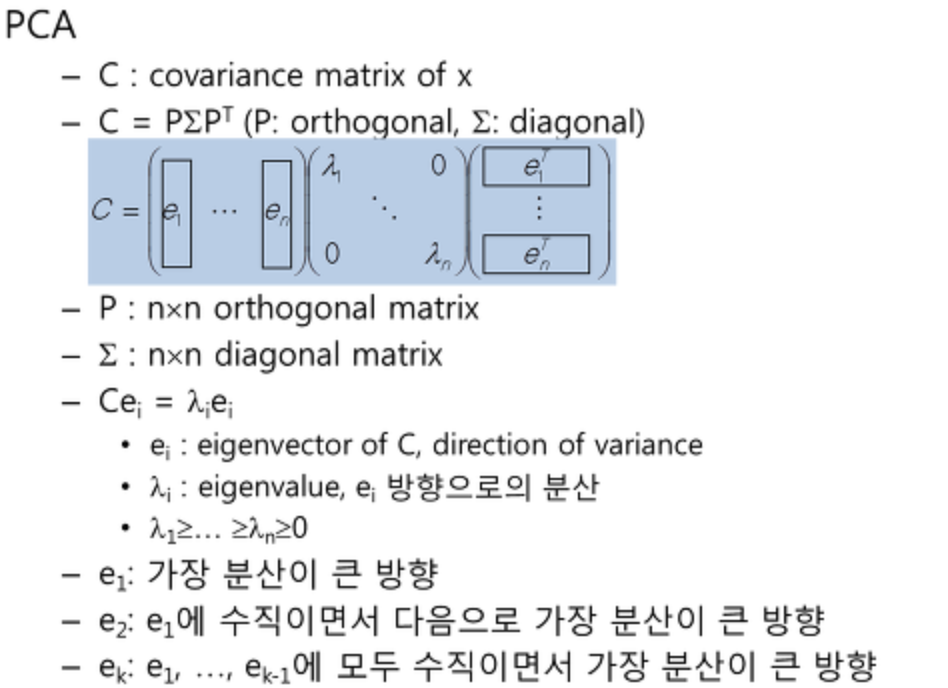
PCA란
Principal Component Analysis의 약자로 분포된 데이터들의 주성분을 찾아내는 방법입니다.
아래와 같이 2차원 좌표에 n개의 데이터가 분포할 때 데이터들의 분포 특성을 2개의 벡터 e1,e2로 가장 잘 설명할 수 있는 방법이 무엇인가를 파악해내는 것입니다.
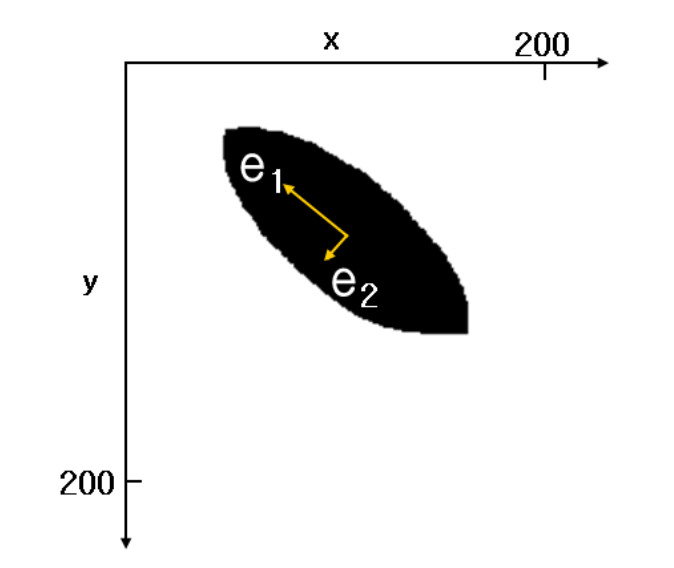
여기서 e1의 방향과 크기, 그리고 e2의 방향과 크기를 알면 데이터의 분포가 어떤 형태인지를 가장 단순하면서도 효과적으로 파악할 수 있습니다.
PCA는 데이터 하나하나에 대해서 성분을 분석하는 게 아니라 여러 데이터들이 모여 하나의 분포를 이룰 때 분포의 주 성분을 분석해주는 방법입니다.
주성분이란
주성분은 그 방향으로 데이터들의 분산이 가장 큰 방향벡터를 의미합니다.
위의 그림으로 보면 e1 방향을 따라 데이터들의 분산이 가장 큽니다. 그리고 e1에 수직이면서 그 다음으로 데이터들의 분산이 큰 방향이 e2입니다.
PCA는 2차원 데이터 집합에 대해 PCA를 수행하면 2개의 서로 수직인 주성분 벡터를 반환하고, 3차원 점들에 대해 PCA를 수행하면 3개의 서로 수직인 주성분 벡터들을 반환합니다.
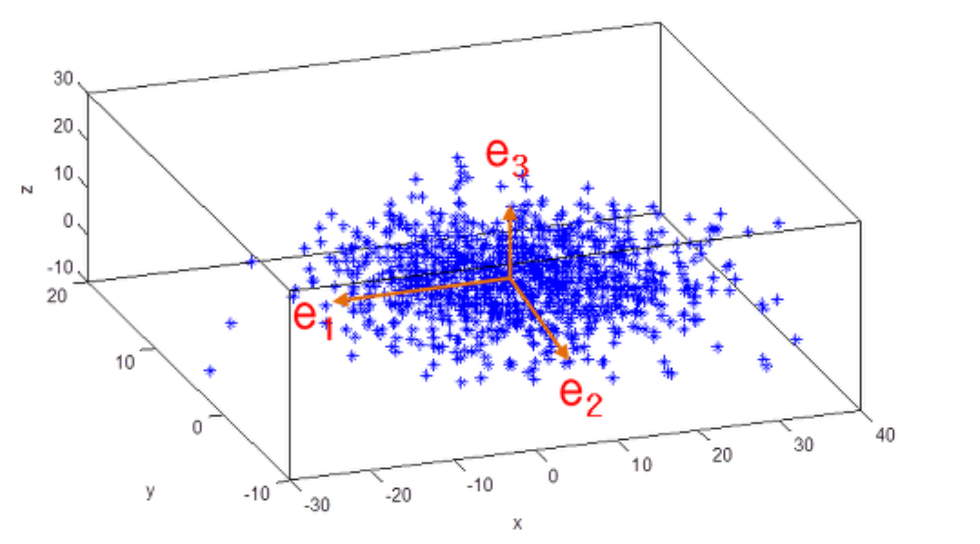
PCA의 활용
1. 분포 데이터 근사 직선
데이터가 분포해있을 때 가장 잘 근사하는 직선의 방정식을 PCA로 구할 수 있습니다.
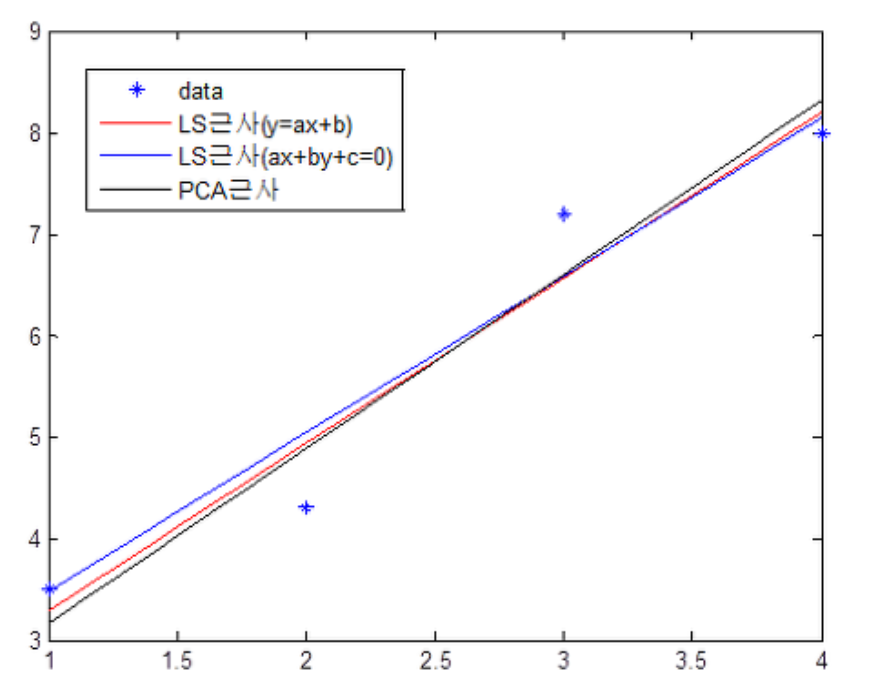
PCA로 직선을 근사하는 방법은 데이터들의 평균 위치를 지나면서 PCA로 나온 제 1 주성분 벡터와 평행인 직선을 구하면 됩니다.
위의 그림을 보면 4개의 데이터를 근사하는 PCA근사와 LS(최소 자승법)근사가 상이합니다.
그 이유는 최소자승법은 직선과 데이터와의 거리를 최소화하는 반면 PCA는 데이터의 분산이 가장 큰 방향을 구하기 때문입니다.
2. 영상 인식
PCA가 영상인식에 활용되는 대표예시는 얼굴인식입니다.
이와 관련한 용어가 eigenface인데요 얼굴 이미지가 있을 떄(45x40, 20개) 이미지에서 픽셀 밝기값을 일렬로 연결하여 벡터로 만들면 이들 각각의 얼굴이미지는 45x40=1800차원의 벡터로 생각할 수 있습니다.
이 20개의 1800차원의 점 데이터를 가지고 PCA를 수행하면 데이터의 차원 수와 동일한 개수의 주성분 벡터를 얻을 수 있습니다.
이렇게 얻어진 주성분 벡터들을 다시 이미지로 해석한 것이 eigenface입니다.
이 중 분산이 큰 순서대로 정렬하여 영향이 큰 주성분을 파악할 수 있죠.
실제 이미지 주성분 값을 보면 다음과 같은데요.

그림에서도 알 수 있듯이 앞부분은 eigenface은 데이터들의 공통된 요소를 나타내고 뒤로 갈수록 세부적인 차이 정보를 나타냅니다. 더 위는 노이즈성 정보이구요.
앞서 PCA의 주성분 벡터들은 서로 수직이라고 했는데요 이 말은 즉 주성분 벡터들이 n차원 공간을 생성하는 기지 역할을 할 수 있음을 의미합니다.
따아서 PCA로 얻은 주성분 벡터들은 e1, e2, ..., en라면 임의의 n차원 데이터 x는 x = c1e1 + c2e2 + ... + cnen과 같이 ei들의 일차결합으로 표현될 수 있습니다.
그런데, 뒷부분의 주성분 벡터들은 데이터 분포에 포함된 노이즈(noise)성 정보를 나타내기 때문에 뒷부분은 버리고 전반부 k개의 주성분 벡터들만을 가지고 원래 데이터를 표현하면 노이즈가 제거된 데이터를 얻을 수 있습니다.
즉, 원래의 x가 x = c1e1 + c2e2 + ... + cnen일 때 xk = c1e1 + ... +ckek로 x를 근사하는 것이죠.

PCA의 계산
PCA를 알기 이ㅜ해서는 먼저 공분산 행렬을 먼저 알아야합니다.
공분산
공분산의 식은 다음입니다.
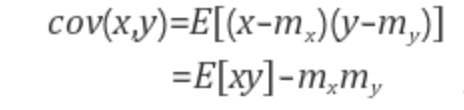
x의 분산은 x들이 평균을 중심으로 얼마나 흩어져 있는지를 나타내고,
x와 y의 공분산은 x,y의 흩어진 정도가 얼마나 서로 상관관계를 가지고 흩어져있는지를 나타냅니다.
가령, x와 y 각각의 분산은 일정한데 x가 mx보다 클 때 y도 my보다 크면 공분산은 최대가 되고, x가 mx보다 커질 때 y는 my보다 작아지면 공분산은 최소, 서로 상관관계가 없으면 공분산은 0이 됩니다.
공분산 행렬
공분산 행렬이란 데이터의 좌표 성분들 사이의 공분산 값을 원소로 하는 행렬로서 데이터의 i번째 좌표 성분과 j번째 좌표 성분의 공분산 값을 행렬의 i행 j열 원소값으로 하는 행렬입니다.

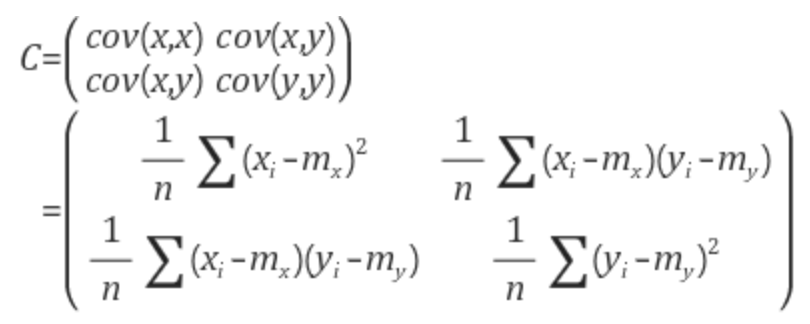
PCA란 한마디로 입력 데이터들의 공분산 행렬에 대해 고유값 분해라고 볼 수 있습니다.
고유값과 고유벡터
행렬 A를 선형변환으로 봤을 때, 선형변환 A에 의한 변환 결과가 자기 자신의 상수배가 되는 0이 아닌 벡터를 고유벡터라고 하고 이 상수배를 고유값이라고 합니다.
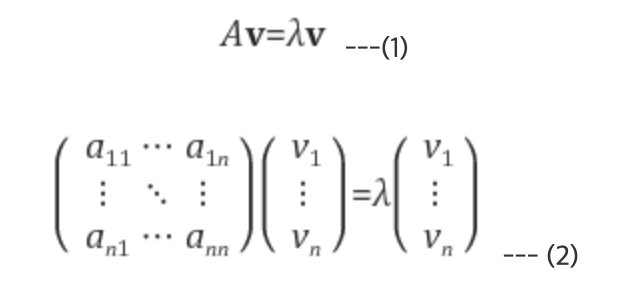
즉, n x n 정방행렬(고유값, 고유벡터는 정방행렬에 대해서만 정의된다) A에 대해 Av = λv를 만족하는 0이 아닌 열벡터 v를 고유벡터, 상수 λ를 고유값이라 정의한다.
어떤 벡터는 이러한 고유값, 고유벡터가 존재하지 않을 수도 있고 어떤 행렬은 하나만 존재하거나 최대 n개까지 존재할 수도 있습니다.
기하학적으로 봤을 때, 행렬 A의 고유벡터는 선형변환 A에 의해 방향은 보존되고 스케일만 변화되는 방향벡터를 나타내고 고유값은 그 고유벡터의 변화되는 스케일 정도를 나타냅니다.
이 때 나오는 고유벡터가 주성분 벡터로 데이터 분포에서 분산이 큰 방향을 나타내고 대응되는 고유값이 그 분산의 크기를 나타냅니다.