정규화는 제약 조건과 더불어 사용되어 구조적인 면에서 무결성을 지키기 위한 방법이다. 정규화는 데이터의 구조적 결함으로 인한 수정, 삭제, 삽입 시의 여러 가지 이상 현상(amomaly)을 해결해준다.
개념 정리
후보키(Candidate Key)
- 후보키는 릴레이션을 구성하는 속성들 중에서 튜플을 유일하게 식별하기 위해 사용하는 속성들의 부분집합, 즉 기본키로 사용할 수 있는 속성들을 말한다.
- 하나의 릴레이션내에서는 중복된 튜플들이 있을 수 없으므로, 모든 릴레이션에는 반드시 하나 이상의 후보키가 존재한다.
- 후보키는 릴레이션에 있는 모든 튜플에 대해서 유일성과 최소성을 만족시켜야 한다.
- 유일성 : 하나의 키값으로 하나의 튜플만을 유일하게 식별할 수 있어야한다.
- 최소성 : 모든 레코드들을 유일하게 식별하는데 꼭 필요한 속성만으로 구성되어 있어야한다.
대체키(Alternate Key)
후보키가 둘 이상일 때 기본키를 제외한 나머지 후보키들을 말한다.
슈퍼키(Super Key)
슈퍼키는 기본키(Primary key)와 마찬가지로 릴레이션을 구성하는 모든 튜플에 대해 유일성을 만족시키지만, 기본키와 달리 최소성은 만족시키지 못한다.
함수 종속
주민등록번호: 결정자
이름, 출생지, 주소: 종속자
주민등록번호는 이름, 출생지, 주소를 결정짓고, 포함하는 개념이다.
이때 이름, 출생지, 주소는 주민등록번호에 함수 종속성을 가지고 있다고 말한다.
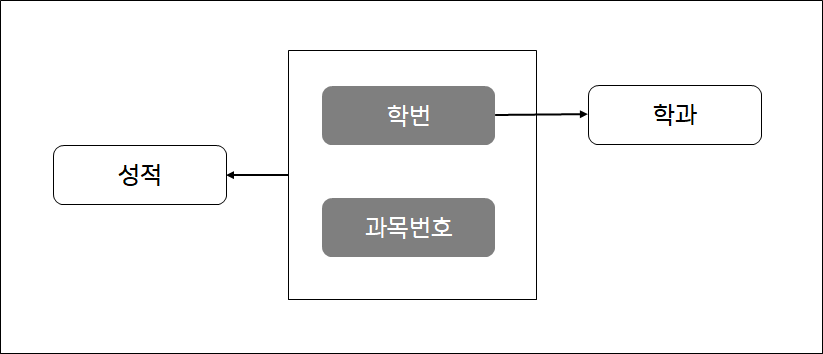
성적은 학번, 과목번호에 완전 함수 종속
학과는 학번에 완전 함수 종속
학과는 학번, 과목번호에 부분 함수 종속
제 1 정규형 - 모든 컬럼이 원자 값으로 이루어져야 한다.
모든 컬럼이 원자 값이 되려면 아래 사항에 해당하지 않아야 한다.
- 모든 컬럼이 반드시 하나의 값을 가져야 하는
다가 속성 - 그리고 하나의 컬럼이 여러 개의 컬럼으로 분리될 수 있는
복합 속성
복합 속성의 경우, 필요로 하는 데이터가 어떤 단위인지에 따라(쿼리의 단위) 개념이 상대적으로 바뀔 수 있다. 예를 들어 성+이름을 합한 데이터를 요하는 경우에는 성+이름이 하나의 속성이 되고, 성과 이름을 따로 요하는 경우에는 복합 속성이 되므로 이를 두 개의 컬럼으로 분리해줘야 한다.
제 2 정규형 - 모든 일반 속성들은 Primary key에 종속적이어야 한다.
Primary key가 아닌 일반 속성들은 N개의 Primary key에 완전 함수 종속이어야하는데, 부분 함수 종속인 일반 속성이 있는 경우 이를 다른 릴레이션으로 분리(무손실 분해)해줘야 한다.
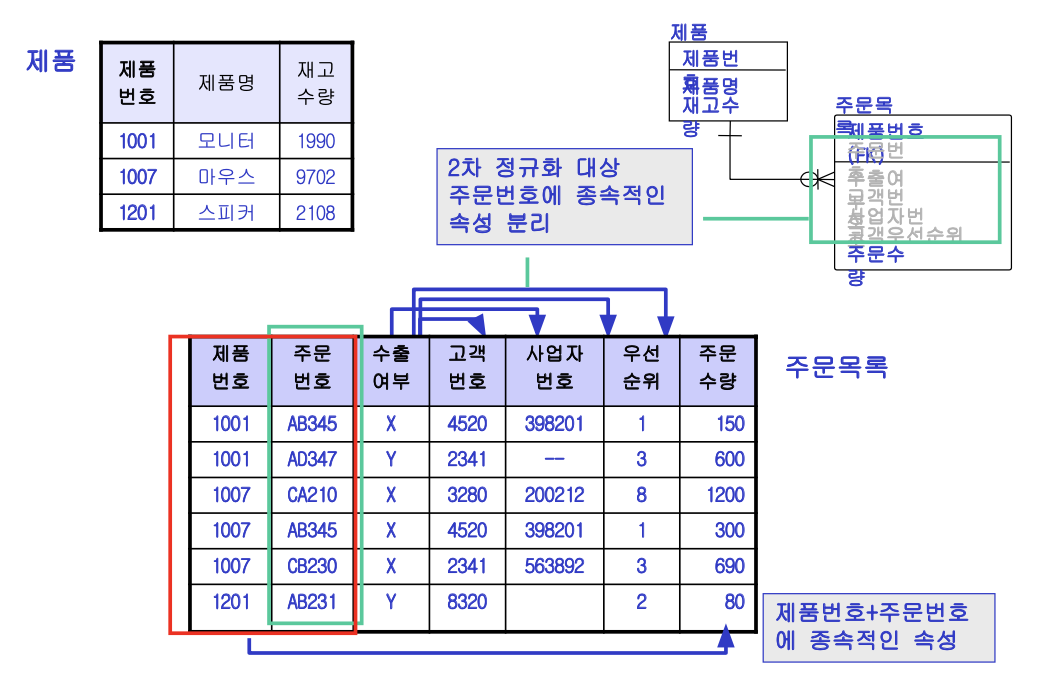
분해 결과 릴레이션은 아래와 같다.
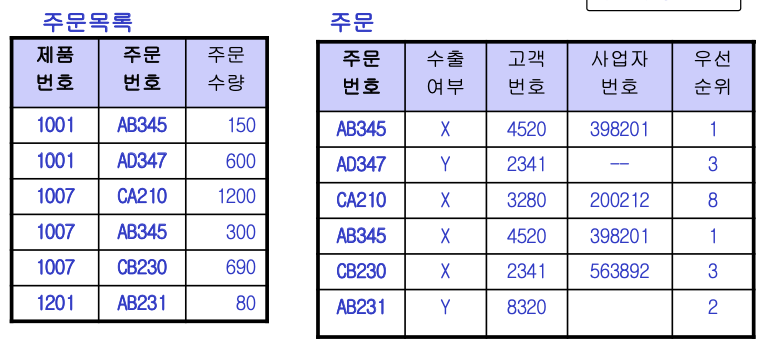
제 3 정규형 - 일반 속성이면서 결정자 역할을 하는 것들을 분리해야 한다.
일반 속성이면서 다른 속성을 결정짓는 역할(결정자 역할)을 하는 속성들이 있는 경우,
이 릴레이션에는 이행적 함수 종속이 존재한다고 말한다.
(A가 B를 결정짓고, B가 C를 결정 짓는 경우)
즉 이행적 함수 종속(TD, Transitive Dependancy)을 다른 릴레이션로 분리하면 3NF가 된다.
보이스/코드 정규형(BCNF) - 강한 제 3 정규형
앞의 정규형들은 Codd의 원론적 정의로, 하나의 후보 키(기본 키)만 가진 것으로 정의하였다. 따라서, 제 3 정규형 정의는 릴레이션이 복수의 후보 키를 갖는 경우에는 적용되지 않는다.
그렇기 때문에 릴레이션이 복수의 후보 키를 갖는 일반적인 경우에도 적용할 수 있는 보이스/코드 정규형이 제안되었다. 즉 BCNF에 속하는 릴레이션은 모두 3NF이지만, 3NF에 속하는 릴레이션이 모두 BCNF는 아니다.
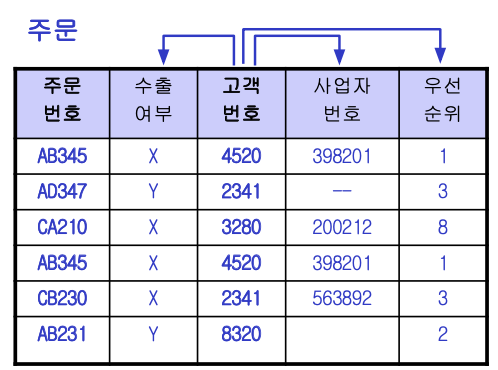
위의 테이블에서 결정자를 모두 키(후보 키)로 하여 테이블을 분리한 결과는 아래와 같다.
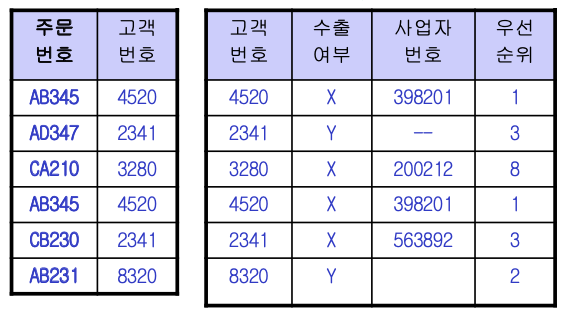
cf)
3NF와 보이스 코드 정규형의 차이는 원론적인 부분이 크기 때문에, 둘 다 통틀어서 일반 속성이면서 결정자의 역할을 하는 것을 새로운 테이블로 분리시켜주면 된다는 정도로 이해하고 있으면 좋을 것 같다.
cf) 이원 릴레이션
R1 (학번, 이름)
R2 (과목 번호, 과목 이름)
위와 같이 key와 attribute 2개로 이루어진 릴레이션을 이원 릴레이션이라고 한다. 모든 이원 릴레이션은 3NF에 속한다.
제 4 정규형 - 다치 종속 제거
제 4 정규형은 다치 종속을 독립된 릴레이션으로 분리한 것이다. 다치 종속(MVD, Multivalued Dependancy)이란, 결정자 하나에 종속자가 여러 개인 것을 의미한다.
예를 들어,
CPT {과목, 교수, 교재}가 있을 때
과목마다 교수는 하나이지만,
과목마다 교재는 여러 개일 수 있다면,
과목 - 교재는 다치 종속 관계이다.
제 5 정규형 - n 분해 릴레이션
3개 또는 그 이상의 릴레이션으로 분해해야만 정보 무손실 분해가 되는 릴레이션을 n-분해 릴레이션이라고 한다. 이런 릴레이션을 제 5 정규형이라고 하고, 이와 같은 릴레이션이 갖는 제약 조건을 n-way 순환 제약조건(cyclic constraint)이라고 한다.
이런 n-분해 릴레이션은 여러 번의 조인을 통해 원래의 분해 전 릴레이션으로 복구가 되기 때문에 조인의 중간 과정에서 원래 릴레이션에 없던 위조 투플이 생성될 수 있다.
cf) 조인 종속
어떤 릴레이션을 분해하고, 이를 다시 조인했을 때의 결과가 원래의 릴레이션과 같을 때 릴레이션 R은 조인 종속을 만족시킨다고 말한다.
한편, 정규화는 하면 할수록 릴레이션의 갯수가 많아지기 때문에, 테이블들로부터 데이터를 얻을 때 조인을 해야하는 횟수도 많아진다. 따라서 보통의 경우에는 제 3 정규형의 조건까지만 만족시키는 선에서 정규화를 마친다.
