사이킷런(scikit-learn) 시작

scikit-learn 특징

• 다양한 머신러닝 알고리즘을 구현한 파이썬 라이브러리
• 심플하고 일관성 있는 API, 유용한 온라인 문서, 풍부한 예제
• 머신러닝을 위한 쉽고 효율적인 개발 라이브러리 제공
• 다양한 머신러닝 관련 알고리즘과 개발을 위한 프레임워크와 API 제공
• 많은 사람들이 사용하며 다양한 환경에서 검증된 라이브러리

scikit-learn 주요 모듈

estimator API

• 일관성: 모든 객체는 일관된 문서를 갖춘 제한된 메서드 집합에서 비롯된 공통 인터페이스 공유
• 검사(inspection): 모든 지정된 파라미터 값은 공개 속성으로 노출
• 제한된 객체 계층 구조
  • 알고리즘만 파이썬 클래스에 의해 표현
  • 데이터 세트는 표준 포맷(NumPy 배열, Pandas DataFrame, Scipy 희소 행렬)으 로 표현
  • 매개변수명은 표준 파이썬 문자열 사용
• 구성: 많은 머신러닝 작업은 기본 알고리즘의 시퀀스로 나타낼 수 있으며, Scikit-Learn은 가능한 곳이라면 어디서든 이 방식을 사용
• 합리적인 기본값: 모델이 사용자 지정 파라미터를 필요로 할 때 라이브러리가 적절한 기본값을 정의

API 사용 방법

• Scikit-Learn으로부터 적절한 estimator 클래스를 임포트해서 모델의 클래스 선택
• 클래스를 원하는 값으로 인스턴스화해서 모델의 하이퍼파라미터 선택
• 데이터를 특징 배열과 대상 벡터로 배치
• 모델 인스턴스의 fit() 메서드를 호출해 모델을 데이터에 적합
• 모델을 새 데이터에 대해서 적용
  • 지도 학습: 대체로 predict() 메서드를 사용해 알려지지 않은 데이터에 대한 레이블 예측
  • 비지도 학습: 대체로 transform()이나 predict() 메서드를 사용해 데이터의 속성을 변환하거나 추론
    

API 사용 예제

import numpy as np
import matplotlib.pyplot as plt
plt.style.use('seaborn-whitegrid')
#<ipython-input-2-66a077f50fee>:3: MatplotlibDeprecationWarning: The seaborn styles shipped by Matplotlib are deprecated since 3.6, as they no longer correspond to the styles shipped by seaborn. However, they will remain available as 'seaborn-v0_8-<style>'. Alternatively, directly use the seaborn API instead.
#plt.style.use('seaborn-whitegrid')

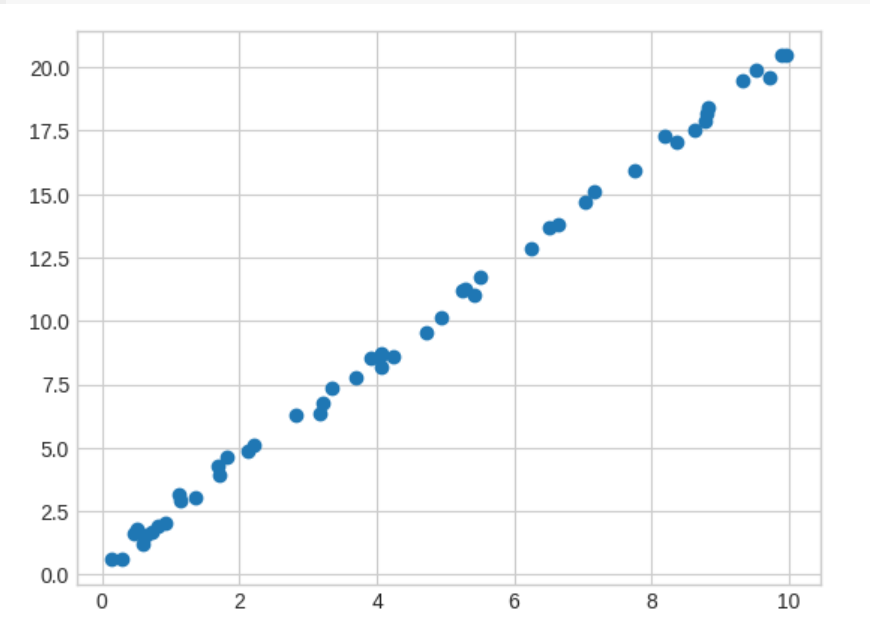
x = 10 * np.random.rand(50)
y = 2 * x + np.random.rand(50)
plt.scatter(x,y);

# 1. 적절한 estimator 클래스를 임포트해서 모델의 클래스 선택
from sklearn.linear_model import LinearRegression # LinearRegression을 import

 # 2. 클래스를 원하는 값으로 인스턴스화해서 모델의 하이퍼파라미터를 선택
model = LinearRegression(fit_intercept=True) #default도 True
model # copy_X = True(입력 데이터를 복사 or not), fit_intercept(상수 형태 값)=True, n_jobs(데이터가 크면 CPU를 병렬로 처리) = None, normalize(정규) = False 

# 3. 데이터를 특정 배열과 대상 벡터로 배치
X = x[:, np.newaxis]
X

# 4. 모델의 인스턴스의 fit() 메서드를 호출해서 모델을 데이터에 적합
model.fit(X, y) #현재 상태를 보여줌

model.coef_
#array([2.01102898])

model.intercept_
#0.43656412446259196  

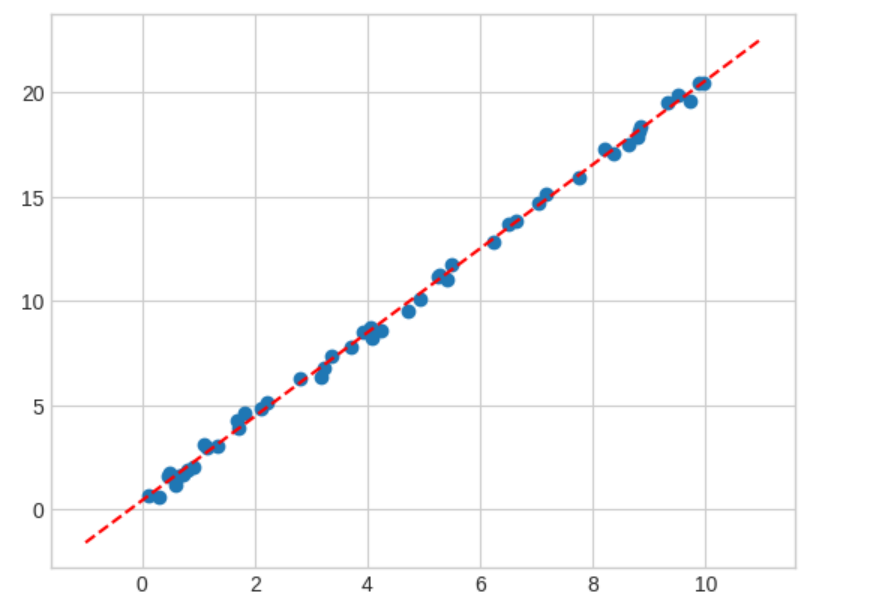
#5. 모델을 새 데이터에 대해서 적용
xfit = np.linspace(-1, 11)
Xfit = xfit[:, np.newaxis]
yfit = model.predict(Xfit)

plt.scatter(x,y)
plt.plot(xfit, yfit, '--r');

예제 데이터 세트

분류 또는 회귀용 데이터 세트

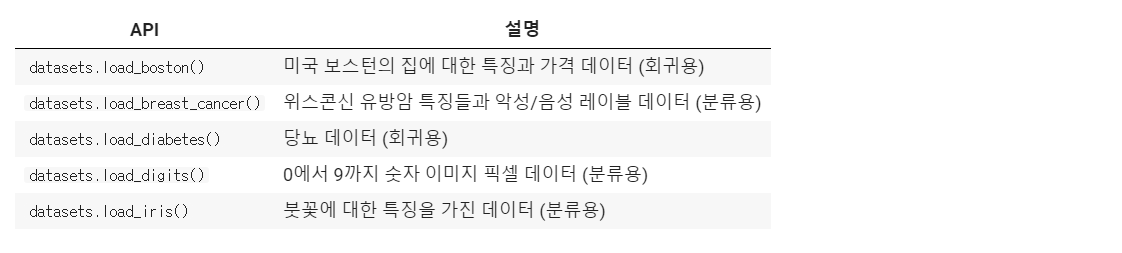
온라인 데이터 세트

• 데이터 크기가 커서 온라인에서 데이터를 다운로드 한 후에 불러오는 예제 데이터 세트
  

분류와 클러스터링을 위한 표본 데이터 생성

예제 데이터 세트 구조

• 일반적으로 딕셔너리 형태로 구성
• data: 특징 데이터 세트
• target: 분류용은 레이블 값, 회귀용은 숫자 결과값 데이터
• target_names: 개별 레이블의 이름 (분류용)
• feature_names: 특징 이름
• DESCR: 데이터 세트에 대한 설명과 각 특징 설명

from sklearn.datasets import load_diabetes
diabetes = load_diabetes()
print(diabetes.keys())
#dict_keys(['data', 'target', 'frame', 'DESCR', 'feature_names', 'data_filename', 'target_filename', 'data_module'])

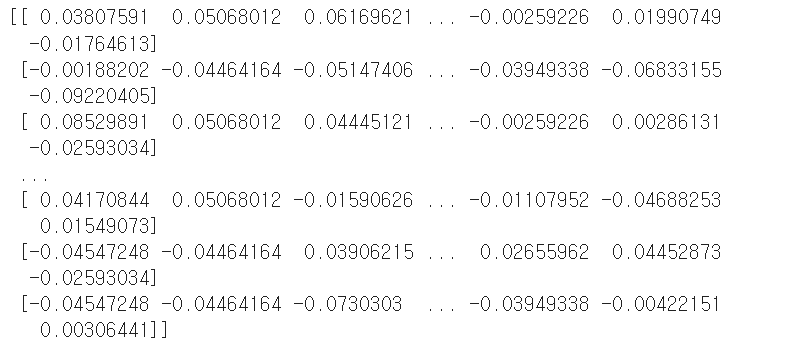
print(diabetes.data)

print(diabetes.target)

print(diabetes.DESCR)

print(diabetes.feature_names)
#['age', 'sex', 'bmi', 'bp', 's1', 's2', 's3', 's4', 's5', 's6']

print(diabetes.data_filename)
print(diabetes.target_filename)
#diabetes_data_raw.csv.gz
#diabetes_target.csv.gz

model_selection 모듈

• 학습용 데이터와 테스트 데이터로 분리
• 교차 검증 분할 및 평가
• Estimator의 하이퍼 파라미터 튜닝을 위한 다양한 함수와 클래스 제공

train_test_split(): 학습/테스트 데이터 세트 분리

from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
from sklearn.datasets import load_diabetes
#
diabetes = load_diabetes()
X_train, X_test, y_train, y_test = train_test_split(diabetes.data, diabetes.target, test_size =0.3)
#
model = LinearRegression()
model.fit(X_train, y_train)
#
print("학습 데이터 점수 : {}".format(model.score(X_train, y_train)))
print("평가 데이터 점수 : {}".format(model.score(X_test, y_test)))
#학습 데이터 점수 : 0.5093006553809074
#평가 데이터 점수 : 0.5195840698115756

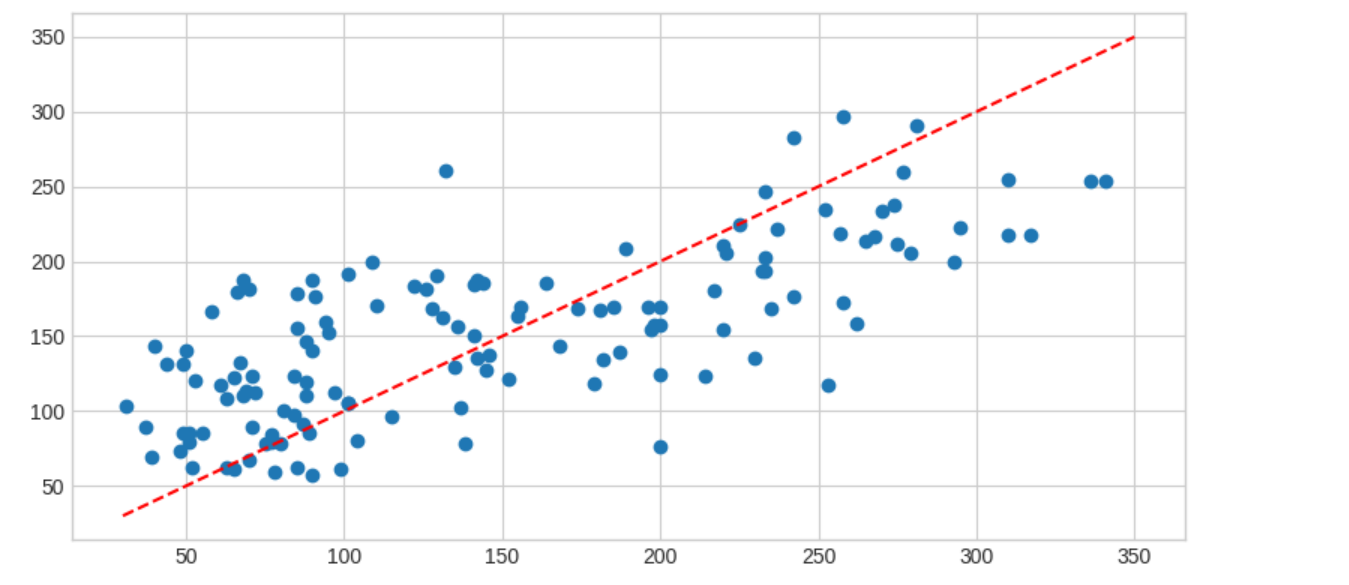
import matplotlib.pyplot as plt
#
predicted = model.predict(X_test)
expected = y_test
plt.figure(figsize = (8,4))
plt.scatter(expected, predicted)
plt.plot([30,350], [30,350], '--r')
plt.tight_layout()

cross_val_score(): 교차 검증

from sklearn.model_selection import cross_val_score, cross_validate
scores = cross_val_score(model, diabetes.data, diabetes.target, cv =5)
print("교차 검증 정확도 : {}".format(scores))
print("교차 검증 정확도 : {} +/- {}".format(np.mean(scores), np.std(scores)))
#교차 검증 정확도 : [0.42955615 0.52259939 0.48268054 0.42649776 0.55024834]
#교차 검증 정확도 : 0.48231643590864215 +/- 0.04926857751190387

GridSearchCV: 교차 검증과 최적 하이퍼 파라미터 찾기

• 훈련 단계에서 학습한 파라미터에 영향을 받아서 최상의 파라미터를 찾는 일은 항상 어려운 문제
• 다양한 모델의 훈련 과정을 자동화하고, 교차 검사를 사용해 최적 값을 제공하는 도구 필요

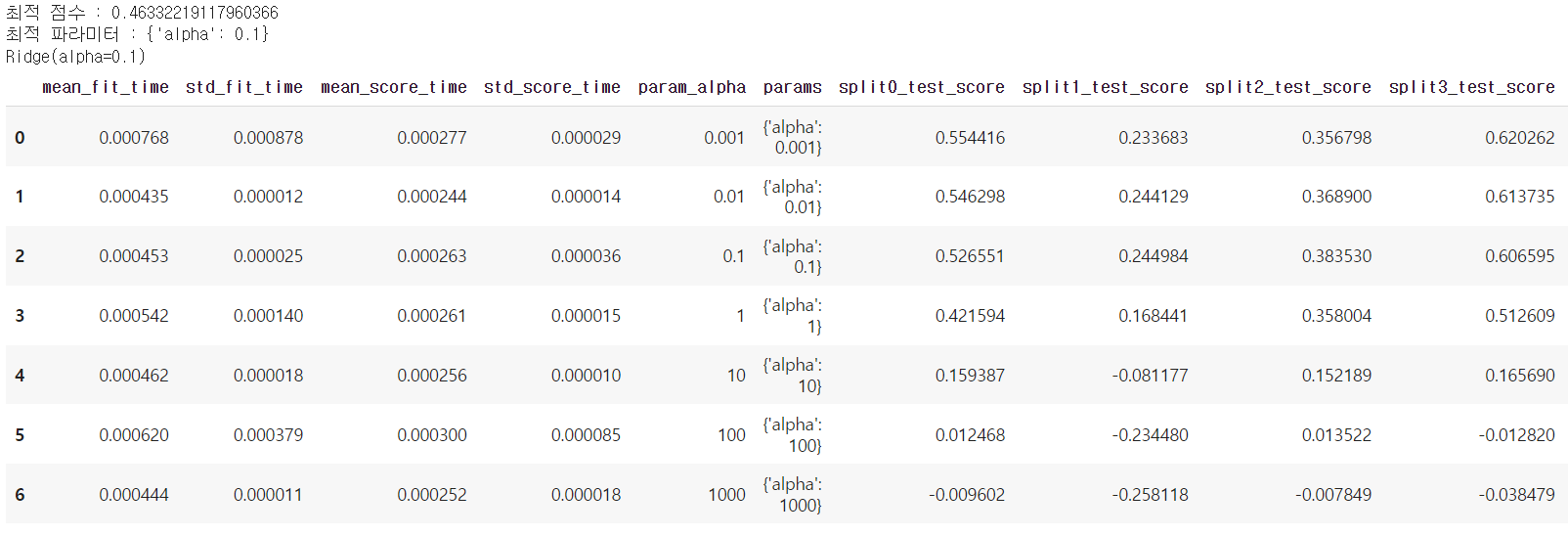
from sklearn.model_selection import GridSearchCV
from sklearn.linear_model import Ridge
import pandas as pd
alpha = [0.001, 0.01, 0.1, 1, 10, 100, 1000]
param_grid = dict(alpha=alpha)
#
gs = GridSearchCV(estimator=Ridge(), param_grid=param_grid, cv=10)
result = gs.fit(diabetes.data, diabetes.target)
#
print("최적 점수 : {}".format(result.best_score_))
print("최적 파라미터 : {}".format(result.best_params_))
print(gs.best_estimator_)
pd.DataFrame(result.cv_results_)

multiprocessing을 이용한 GridSearchCV

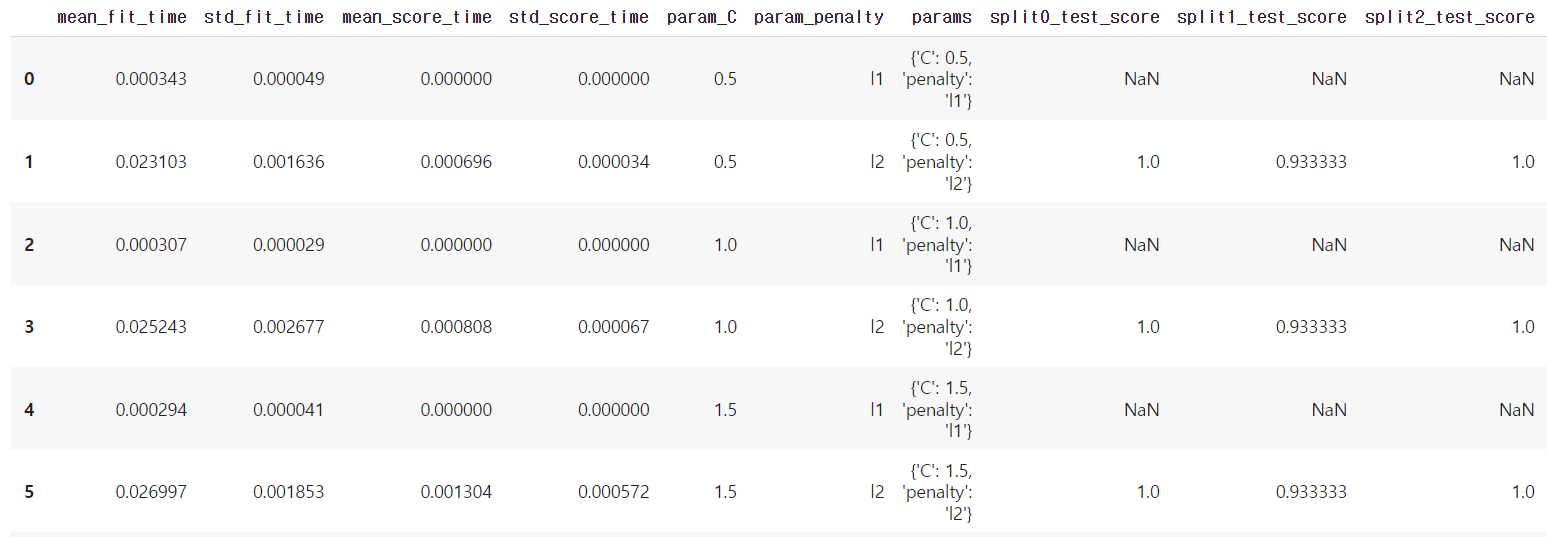
import multiprocessing
from sklearn.datasets import load_iris
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import GridSearchCV
#
iris = load_iris()
#
param_grid = [{ 'penalty' : ['l1', 'l2'],
               'C': [0.5, 1.0, 1.5, 1.8, 2.0, 2.4]}]
#
gs = GridSearchCV(estimator=LogisticRegression(), param_grid=param_grid,
                  scoring = 'accuracy', cv=10, n_jobs=multiprocessing.cpu_count())
result = gs.fit(iris.data, iris.target)
#
print("최적 점수 : {}".format(result.best_score_))
print("최적 파라미터 : {}".format(result.best_params_))
print(gs.best_estimator_)
pd.DataFrame(result.cv_results_)

preprocessing 데이터 전처리 모듈

StandardScaler: 표준화 클래스

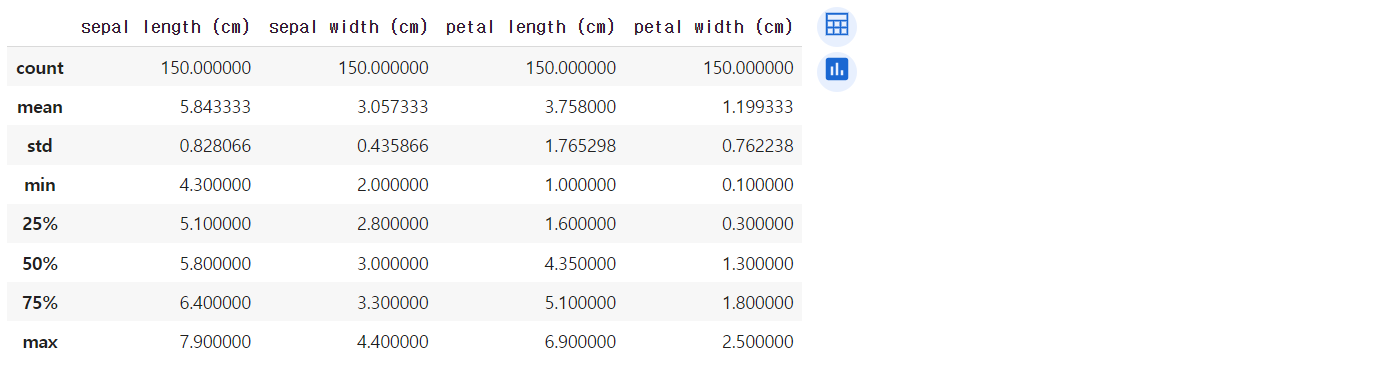
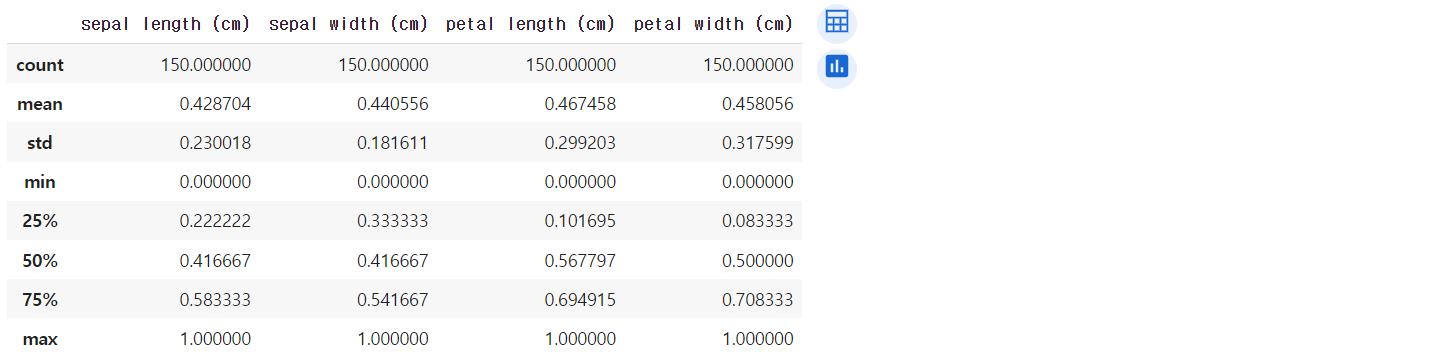
iris = load_iris()
iris_df = pd.DataFrame(data= iris.data, columns=iris.feature_names)
iris_df.describe()

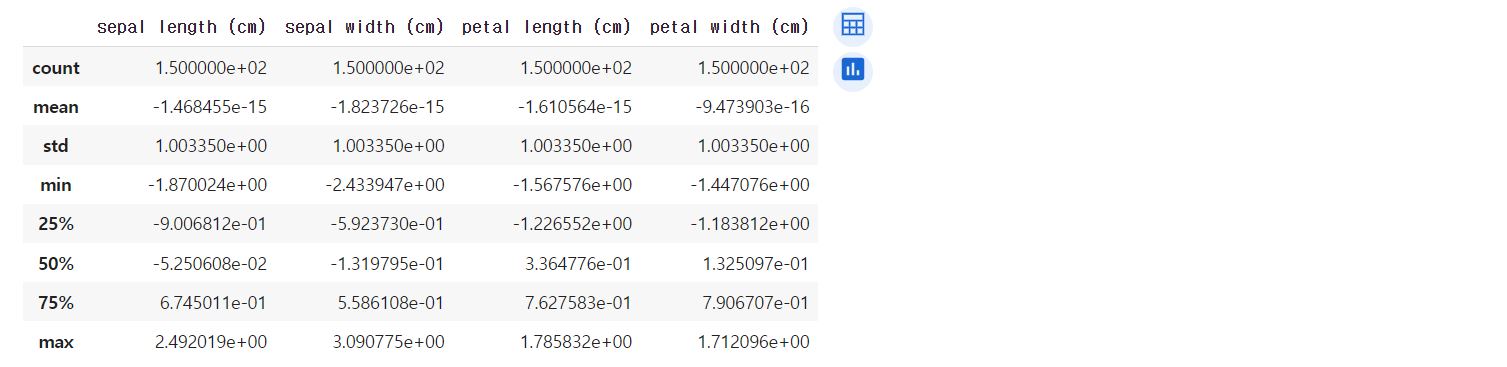
from sklearn.preprocessing import StandardScaler
#
scaler = StandardScaler()
iris_scaled = scaler.fit_transform(iris_df)
iris_df_scaled = pd.DataFrame(data=iris_scaled, columns = iris.feature_names)
iris_df_scaled.describe()

X_train, X_test, y_train, y_test = train_test_split(iris_df_scaled, iris.target, test_size=0.3)
model = LogisticRegression()
model.fit(X_train, y_train)
#
print("훈련 데이터 점수 : {}".format(model.score(X_train, y_train)))
print("평가 데이터 점수 : {}".format(model.score(X_test, y_test)))
#훈련 데이터 점수 : 0.9809523809523809
#평가 데이터 점수 : 0.9333333333333333

MinMaxScaler: 정규화 클래스

from sklearn.preprocessing import MinMaxScaler
#
scaler = MinMaxScaler()
iris_scaled = scaler.fit_transform(iris_df)
iris_df_scaled = pd.DataFrame(data=iris_scaled, columns=iris.feature_names)
iris_df_scaled.describe()

성능 평가 지표

정확도(Accuracy)

• 정확도는 전체 예측 데이터 건수 중 예측 결과가 동일한 데이터 건수로 계산
• scikit-learn에서는 accuracy_score 함수를 제공

from sklearn.datasets import make_classification
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score
#
X,y = make_classification(n_samples = 1000, n_features=2, n_informative=2,
                        n_redundant=0, n_clusters_per_class=1)
#
X_train, X_test, y_train, y_test = train_test_split(X,y, test_size=0.3)
#
model = LogisticRegression()
model.fit(X_train, y_train)
#
print("훈련 데이터 점수 : {}".format(model.score(X_train, y_train)))
print("평가 데이터 점수 : {}".format(model.score(X_test, y_test)))
#
predict = model.predict(X_test)
print("정확도 : {}".format(accuracy_score(y_test, predict)))
#훈련 데이터 점수 : 0.8857142857142857
#평가 데이터 점수 : 0.9133333333333333
#정확도 : 0.9133333333333333

오차 행렬(Confusion Matrix)

• True Negative: 예측값을 Negative 값 0으로 예측했고, 실제 값도 Negative 값 0
• False Positive: 예측값을 Positive 값 1로 예측했는데, 실제 값은 Negative 값 0
• False Negative: 예측값을 Negative 값 0으로 예측했는데, 실제 값은 Positive 값 1
• True Positive: 예측값을 Positive 값 1로 예측했고, 실제 값도 Positive 값 1

from sklearn.metrics import confusion_matrix
#
confmat = confusion_matrix(y_true=y_test, y_pred=predict)
print(confmat)
#[[131  10]
# [ 16 143]]

fig, ax = plt.subplots(figsize=(2.5,2.5))
ax.matshow(confmat, cmap=plt.cm.Blues, alpha=0.3)
for i in range(confmat.shape[0]):
  for j in range(confmat.shape[1]):
    ax.text(x=j, y=i, s=confmat[i,j], va='center', ha='center')
#
#
plt.xlabel('Predicted label')
plt.ylabel('True label')
plt.tight_layout()
plt.show()

정밀도(Precision)와 재현율(Recall)

• 정밀도 = TP / (FP + TP)

• 재현율 = TP / (FN + TP)

• 정확도 = (TN + TP) / (TN + FP + FN + TP)

• 오류율 = (FN + FP) / (TN + FP + FN + TP)

from sklearn.metrics import precision_score, recall_score
#
precision = precision_score(y_test, predict)
recall = recall_score(y_test, predict)
#
print("정밀도 : {}".format(precision))
print("재현율 : {}".format(precision))
#정밀도 : 0.934640522875817
#재현율 : 0.934640522875817

F1 Score(F-measure)

from sklearn.metrics import f1_score
#
f1 = f1_score(y_test, predict)
#
print("F1 score : {}".format(f1))
#F1 score : 0.9166666666666666

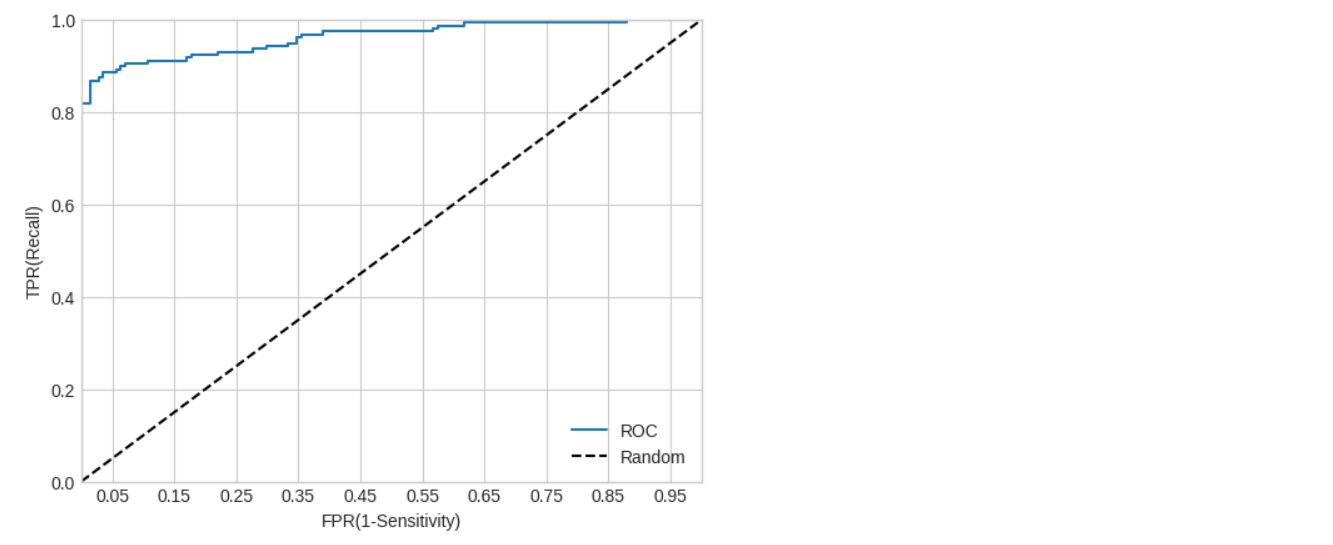
ROC 곡선과 AUC

• ROC 곡선은 FPR(False Positive Rate)이 변할 때 TPR(True Positive Rate)이 어떻게 변하는지 나타내는 곡선

  • TPR(True Positive Rate): TP / (FN + TP), 재현율
  • TNR(True Negative Rate): TN / (FP + TN)
  • FPR(False Positive Rate): FP / (FP + TN), 1 - TNR

• AUC(Area Under Curve) 값은 ROC 곡선 밑에 면적을 구한 값 (1이 가까울수록 좋은 값)

from sklearn.metrics import roc_curve
#
pred_proba_class1 = model.predict_proba(X_test)[:,1]
fprs, tprs, thresholds = roc_curve(y_test, pred_proba_class1)
#
plt.plot(fprs, tprs, label='ROC')
plt.plot([0,1], [0,1], '--k', label='Random')
start, end = plt.xlim()
plt.xticks(np.round(np.arange(start, end, 0.1), 2))
plt.xlim(0,1)
plt.ylim(0,1)
plt.xlabel("FPR(1-Sensitivity)")
plt.ylabel("TPR(Recall)")
plt.legend();

from sklearn.metrics import roc_auc_score
#
roc_auc = roc_auc_score(y_test, predict)
#
print("ROC AUC Score : {}".format(roc_auc))
#ROC AUC Score : 0.9142245416833935