Lecture 01. Matplotlib 특징
1) 파이썬의 대표적인 과학 계산용 그래프 라이브러리
2) 선 그래프, 히스토그램, 산점도 등의 고품질 그래프 제공
3) 저수준 api를 사용한 다양한 시각화 기능 제공
4) 다양한 운영체제와 그래픽 백엔드에서 동작
import matplotlib as npl import matplotlib.pyplot as plt import numpy as np import pandas as pd npl.__version__ #'3.7.1'
plt.style.use(['seaborn-notebook'])
라인 플롯(Line Plot)
1) 플롯(plot)은 그림(figure)와 축(axis)으로 구성
2) plt.Figure : 축과 그래픽, 텍스트, 레이블을 표시하는 모든 객체를 포함하는 컨테이너
3) plt.Axes : 눈금과 레이블이 있는 테두리 박스로 시각화를 형성하는 플롯 요소를 포함
fig = plt.figure() ax = plt.axes() #일반적인 그래프를 보여줍니다.
fig = plt.figure() plt.plot([0,0.2,0.4,0.6,0.8,1]*5);
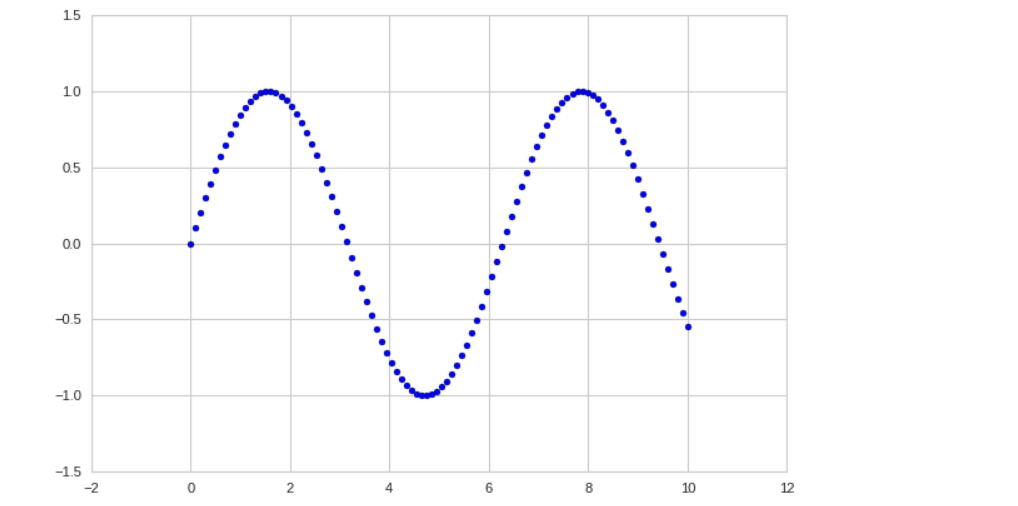
x = np.arange(0,10,0.01) #곡선 그래프 fig = plt.figure() plt.plot(x, np.sin(x));
plt.plot(x, np.sin(x)); plt.plot(x, np.cos(x));
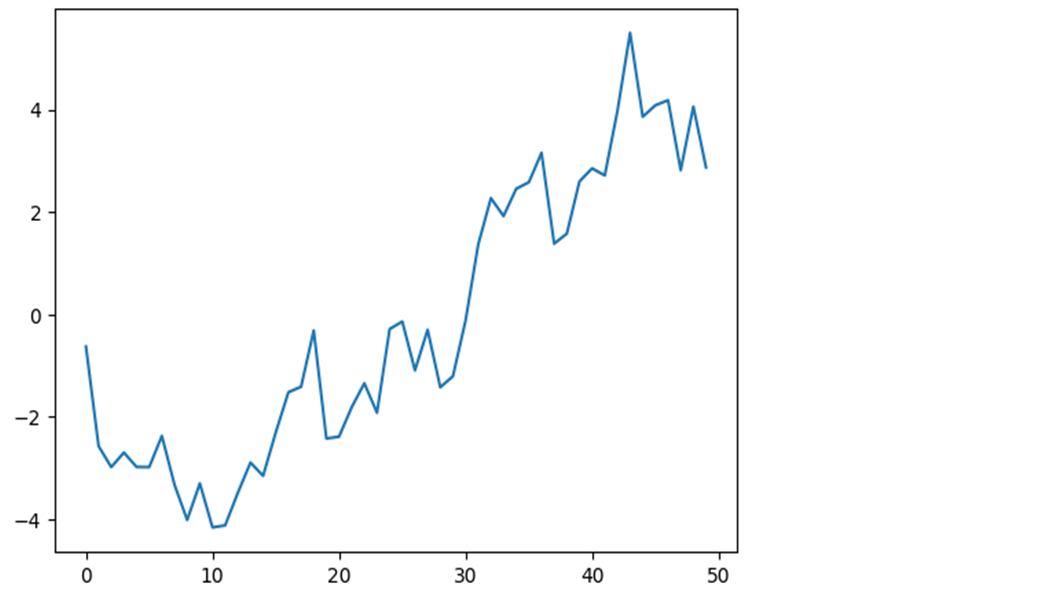
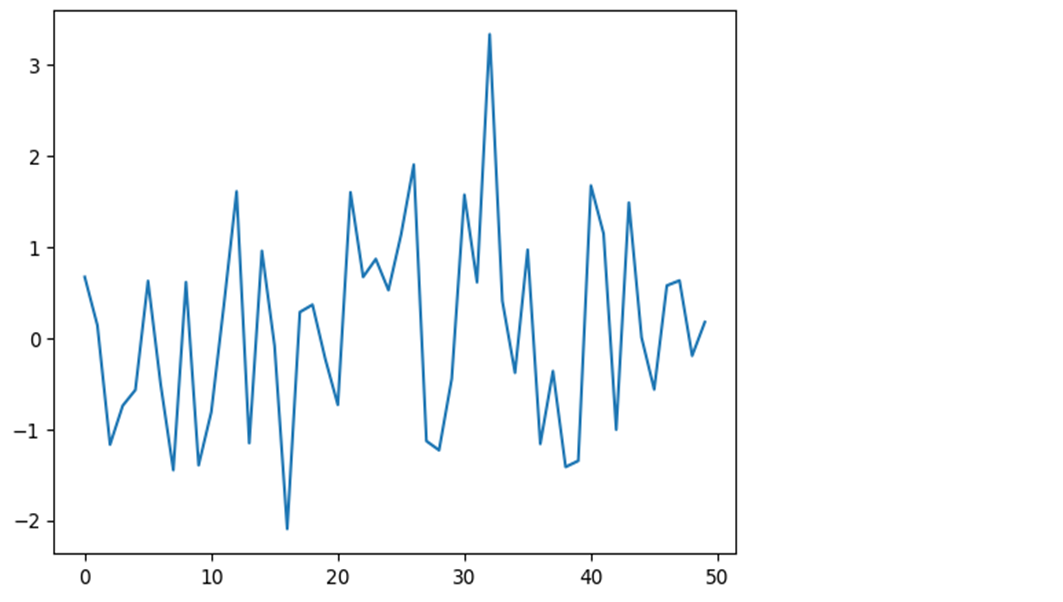
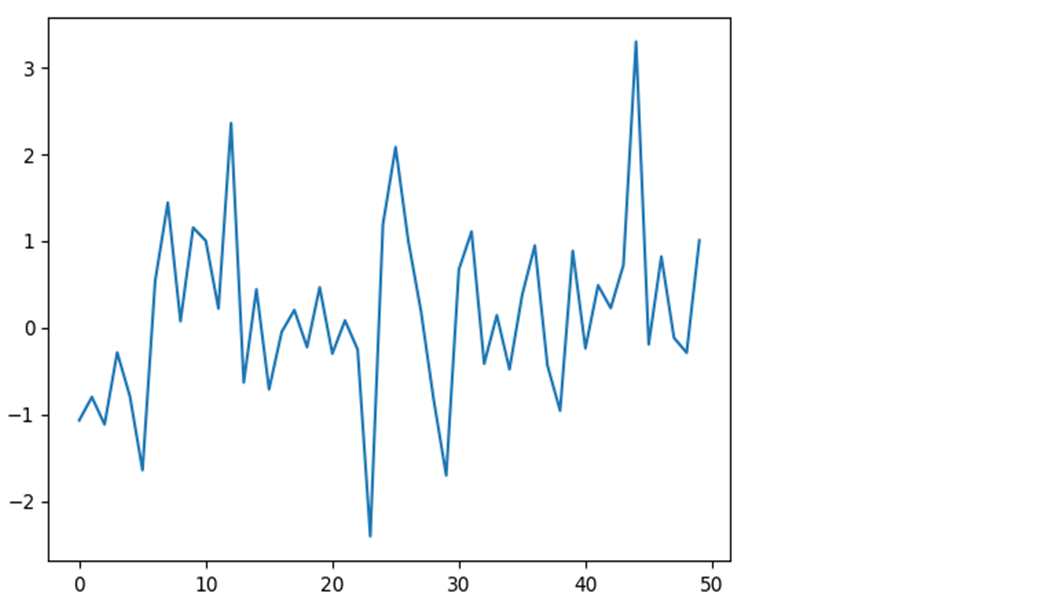
plt.plot(np.random.randn(50).cumsum())
라인 스타일(Line Style)
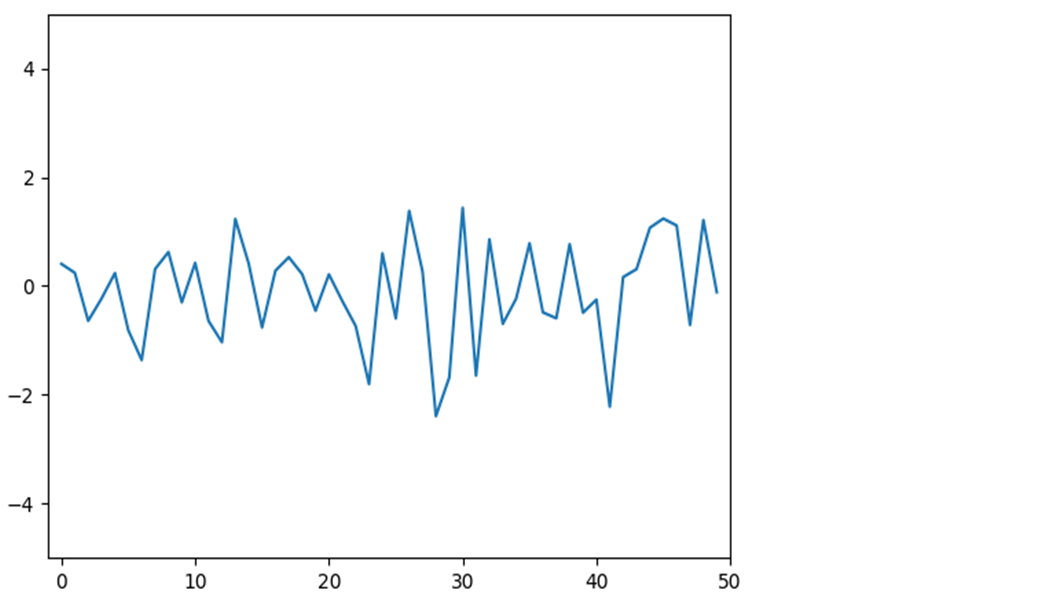
plt.plot(np.random.randn(50).cumsum(), linestyle='solid')
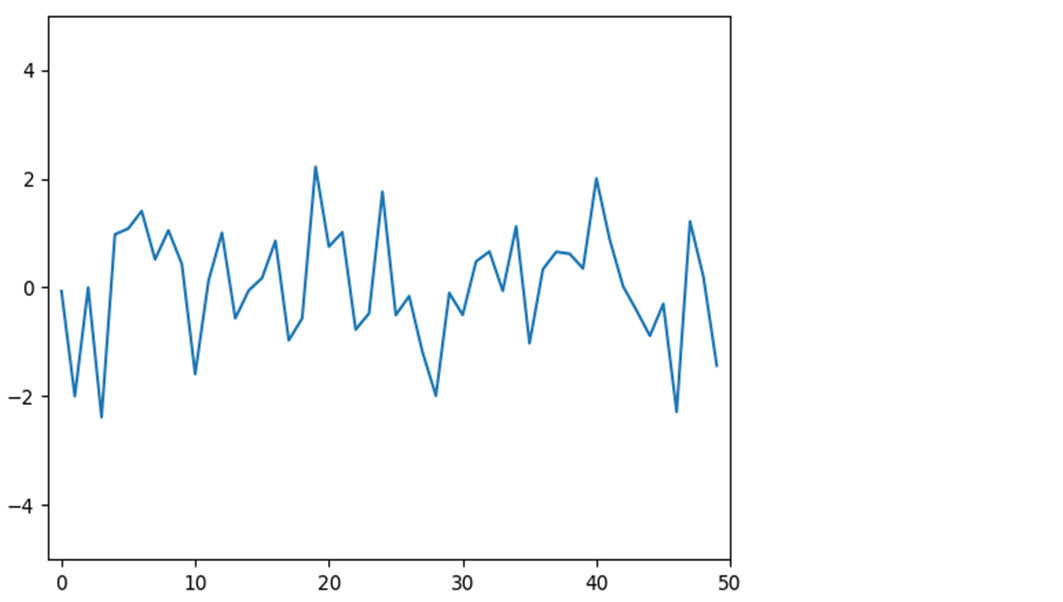
plt.plot(np.random.randn(50).cumsum(), linestyle='dashed')
plt.plot(np.random.randn(50).cumsum(), linestyle='dashdot')
plt.plot(np.random.randn(50).cumsum(), linestyle='dotted')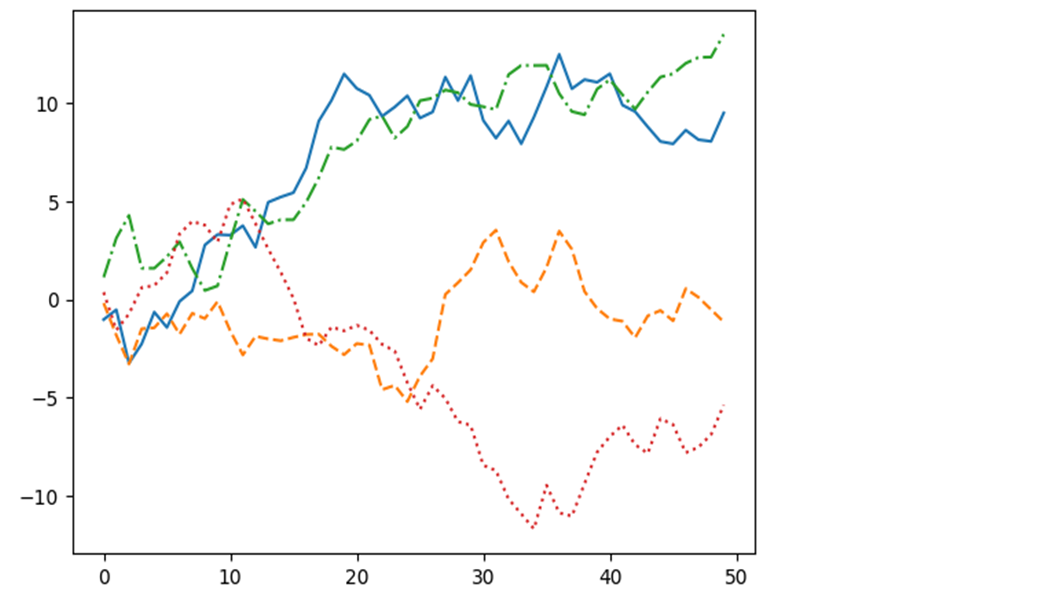
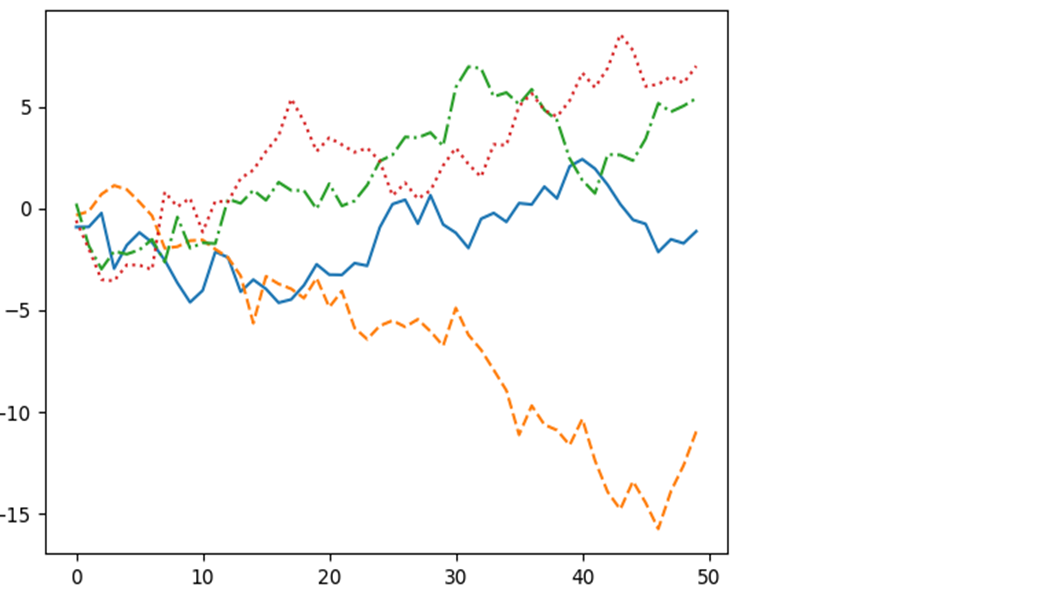
plt.plot(np.random.randn(50).cumsum(), linestyle='-') plt.plot(np.random.randn(50).cumsum(), linestyle='--') plt.plot(np.random.randn(50).cumsum(), linestyle='-.') plt.plot(np.random.randn(50).cumsum(), linestyle=':')
색상 스타일(Color Style)
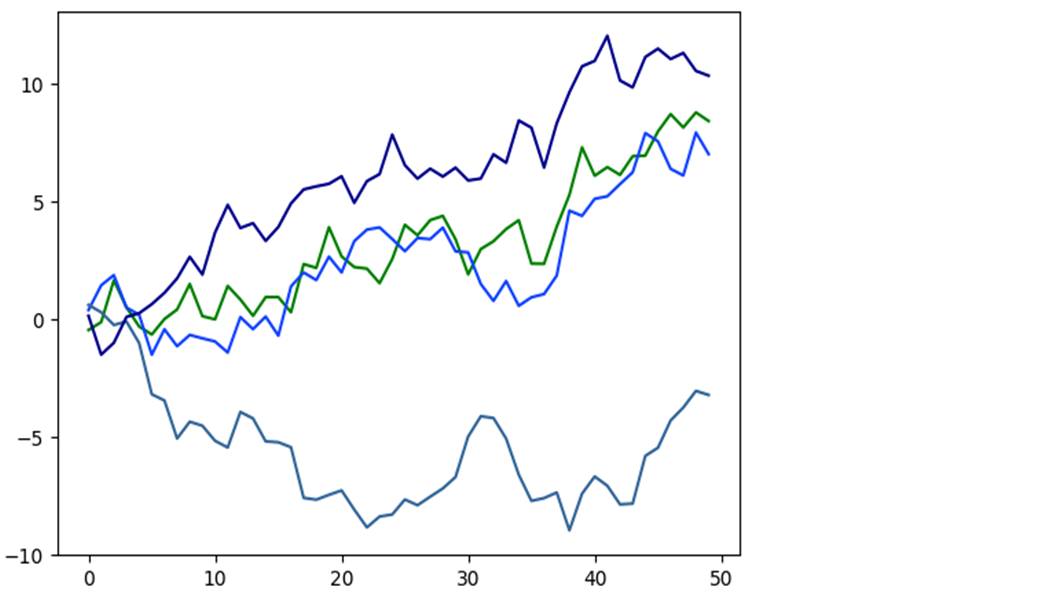
plt.plot(np.random.randn(50).cumsum(), color='g') plt.plot(np.random.randn(50).cumsum(), color='#1243FF') plt.plot(np.random.randn(50).cumsum(), color=(0.2, 0.4, 0.6)) plt.plot(np.random.randn(50).cumsum(), color='darkblue')
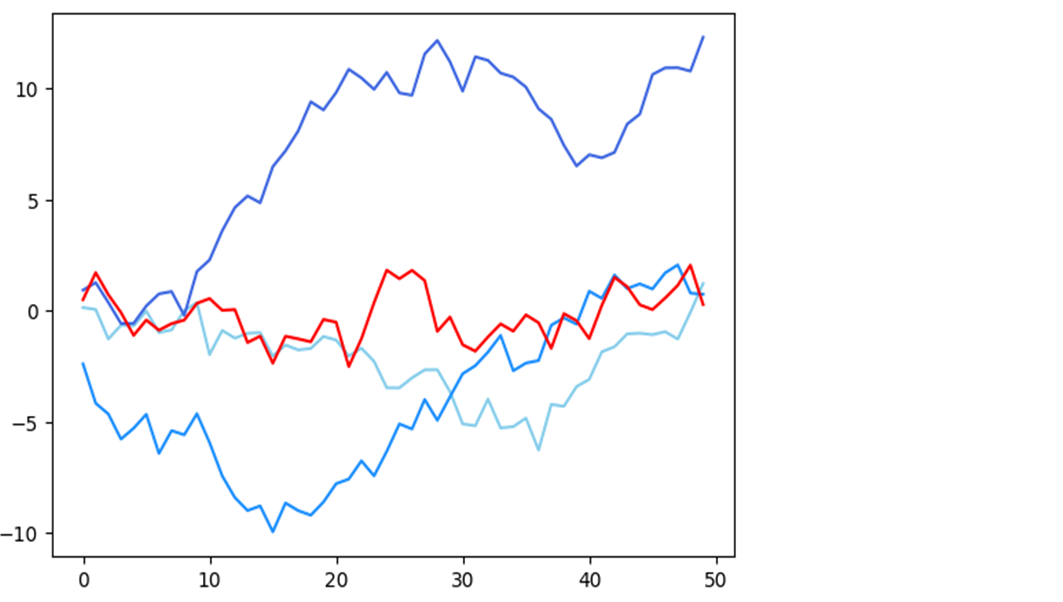
plt.plot(np.random.randn(50).cumsum(), color='skyblue') plt.plot(np.random.randn(50).cumsum(), color='dodgerblue') plt.plot(np.random.randn(50).cumsum(), color='royalblue') plt.plot(np.random.randn(50).cumsum(), color='red')
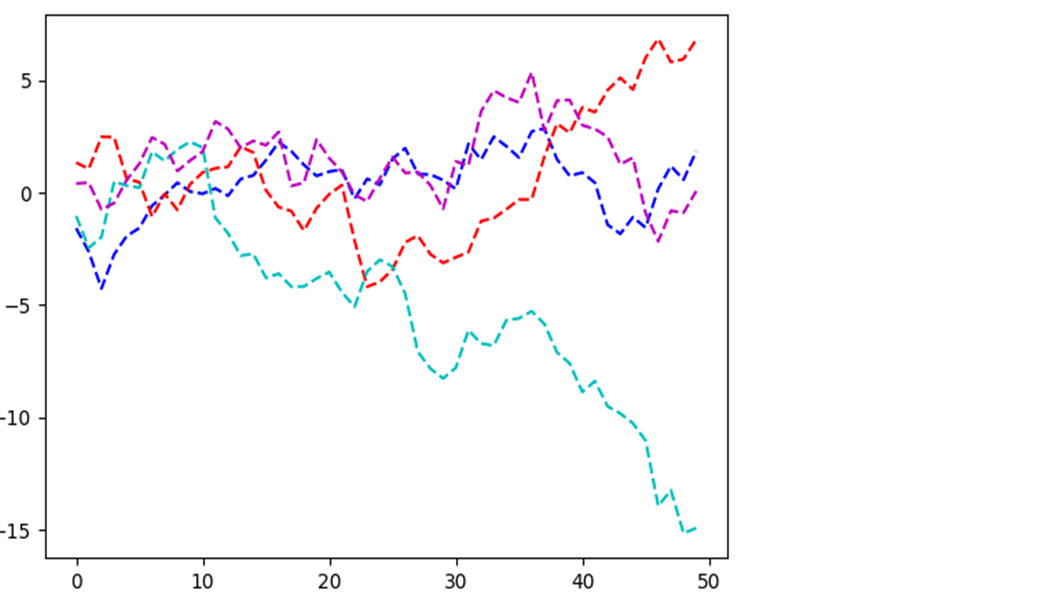
plt.plot(np.random.randn(50).cumsum(), 'b--') plt.plot(np.random.randn(50).cumsum(), 'r--') plt.plot(np.random.randn(50).cumsum(), 'c--') plt.plot(np.random.randn(50).cumsum(), 'm--')
플롯 축(Plot Axis)
plt.plot(np.random.randn(50));
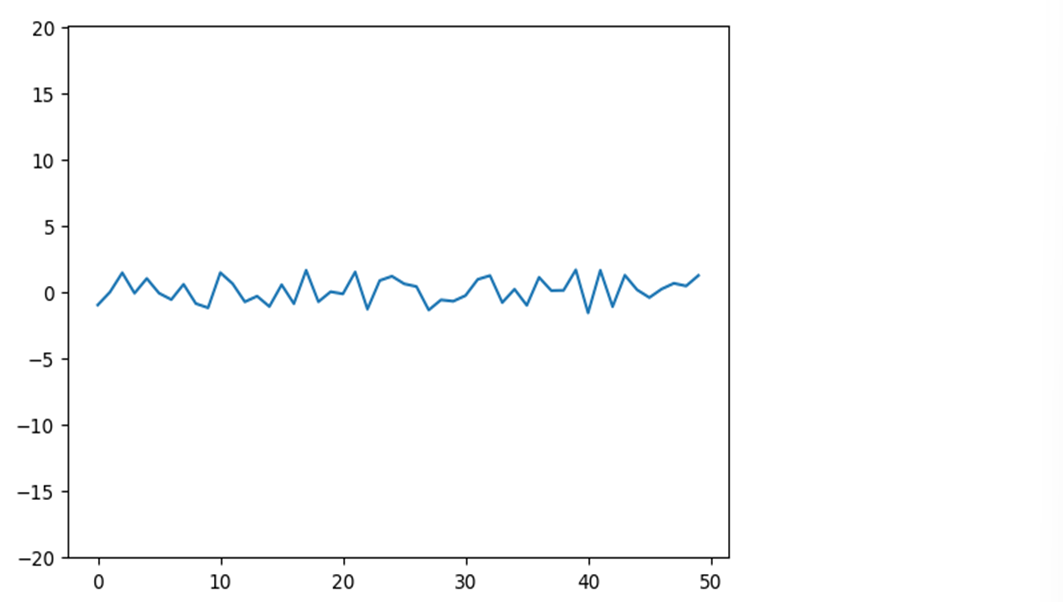
plt.plot(np.random.randn(50)) plt.xlim(-1,50) plt.ylim(-5,5);
plt.plot(np.random.randn(50)) plt.axis([-1, 50,-5, 5]);
plt.plot(np.random.randn(50)) plt.axis('tight');
plt.plot(np.random.randn(50)) plt.axis('equal');
플롯 레이블(Plot Label)
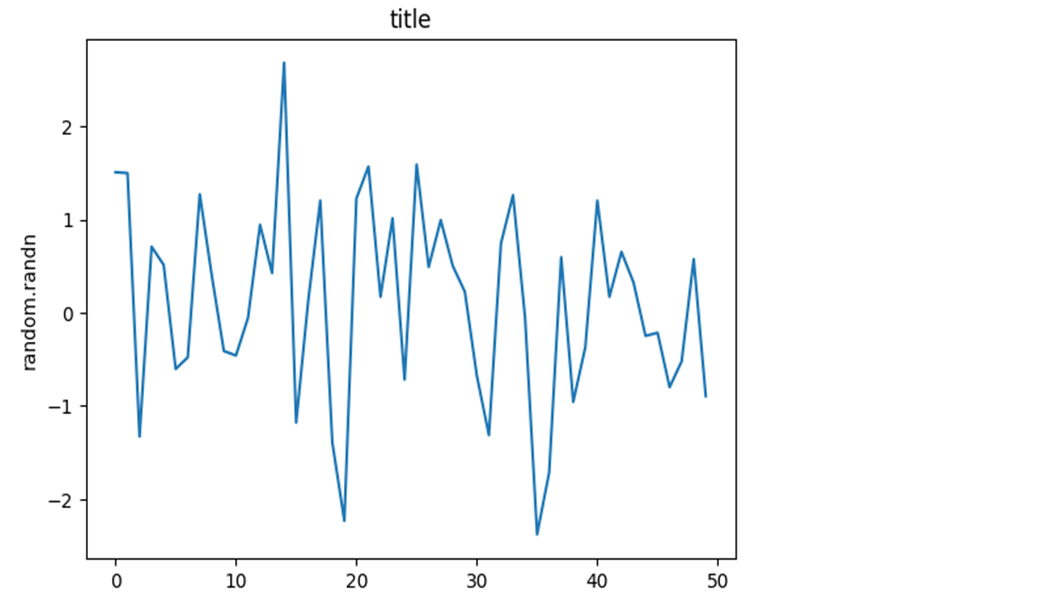
plt.plot(np.random.randn(50)) plt.title("title") plt.xlabel("x") plt.ylabel("random.randn")
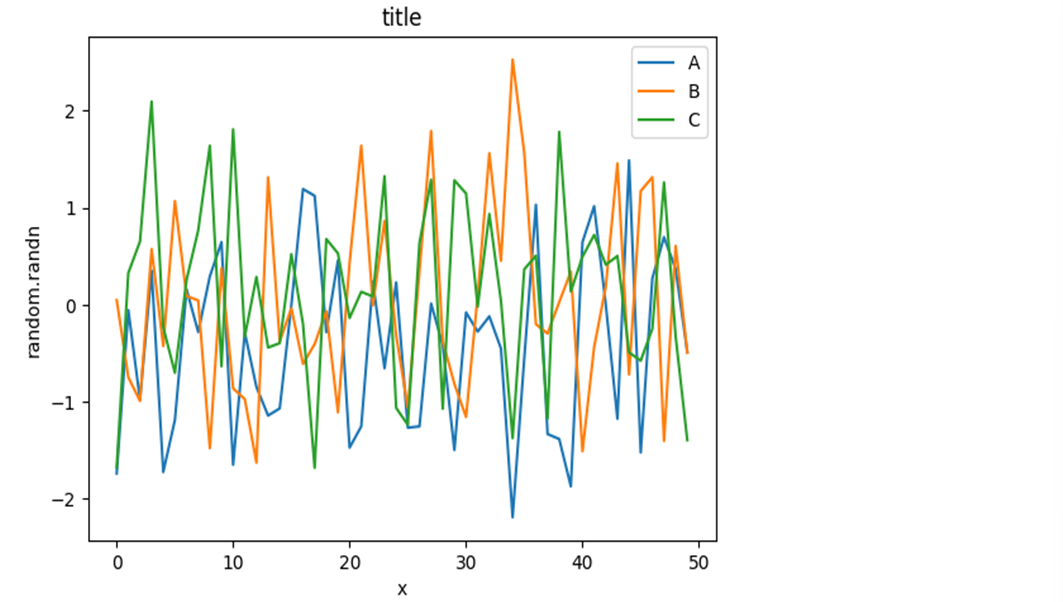
plt.plot(np.random.randn(50), label='A') plt.plot(np.random.randn(50), label='B') plt.plot(np.random.randn(50), label='C') plt.title("title") plt.xlabel("x") plt.ylabel("random.randn") plt.legend();
폰트 관리자(Font Manager)
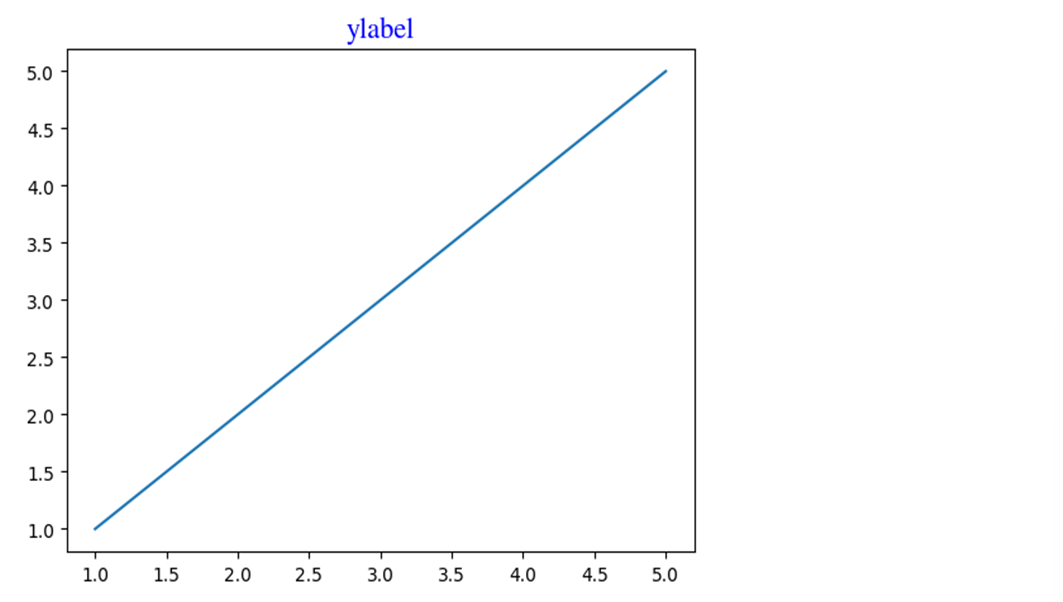
set([f.name for f in npl.font_manager.fontManager.ttflist])font1 = {"family": "cmr10", 'size':24, 'color': 'blue'} font2 = {"family": "Liberation Mono", 'size':18, 'weight':'bold', 'color': 'blue'} font3 = {"family": "STIXGeneral", 'size':16, 'weight':'light', 'color': 'blue'} plt.plot([1,2,3,4,5], [1,2,3,4,5]) plt.title('title', fontdict=font1) plt.title('xlabel', fontdict=font2) plt.title('ylabel', fontdict=font3);
해당 폰트가 없어서 default 값으로 출력된다. 글꼴이 적용된다는 것만 알고 넘어가도록 한다.
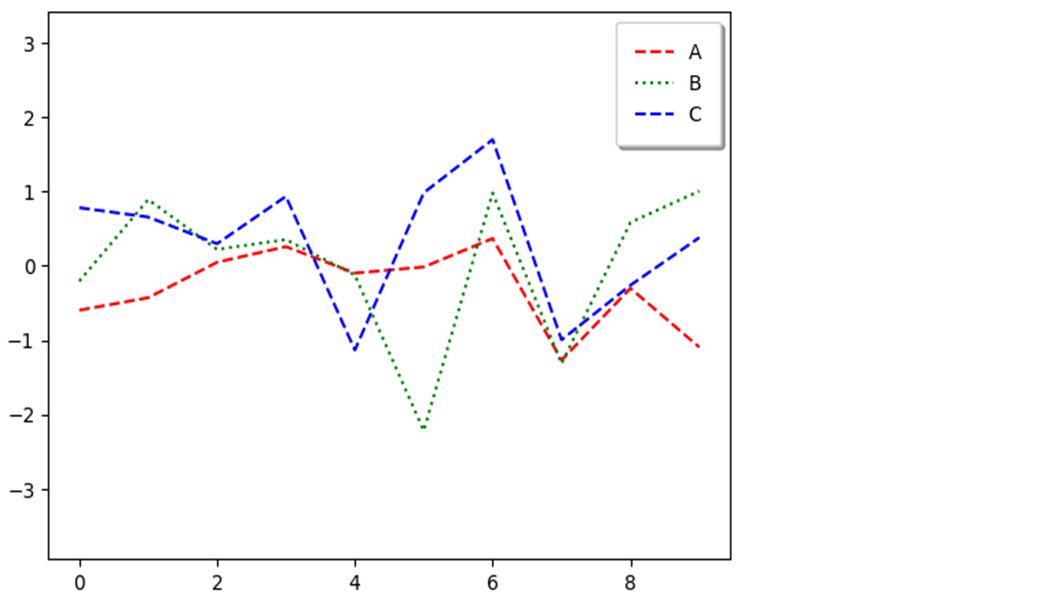
플롯 범례(Plot Legend)
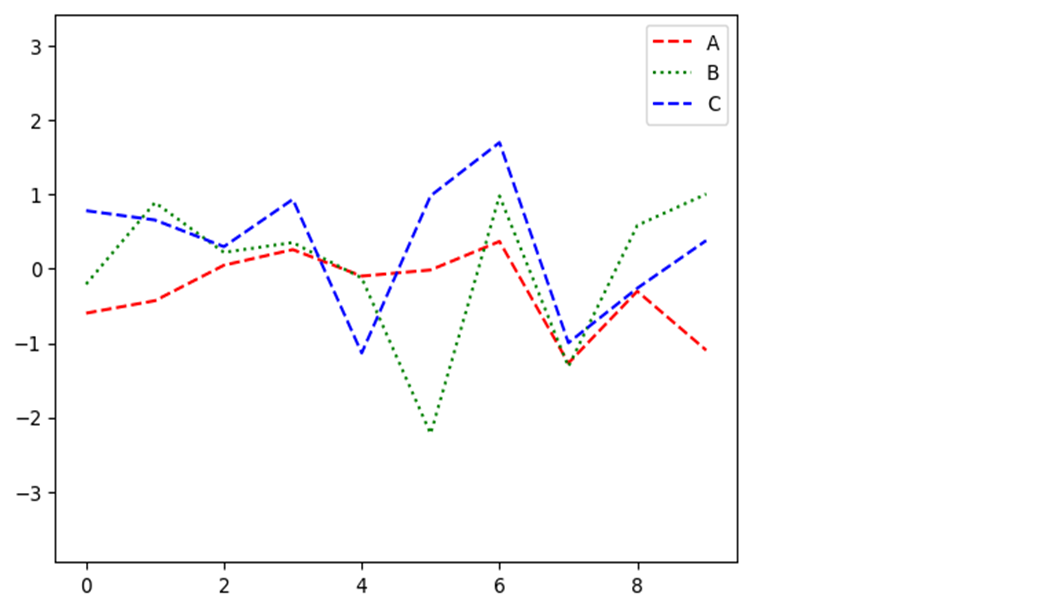
fig, ax = plt.subplots() ax.plot(np.random.randn(10), '--r', label='A') ax.plot(np.random.randn(10), ':g', label='B') ax.plot(np.random.randn(10), '--b', label='C') ax.axis('equal') ax.legend();
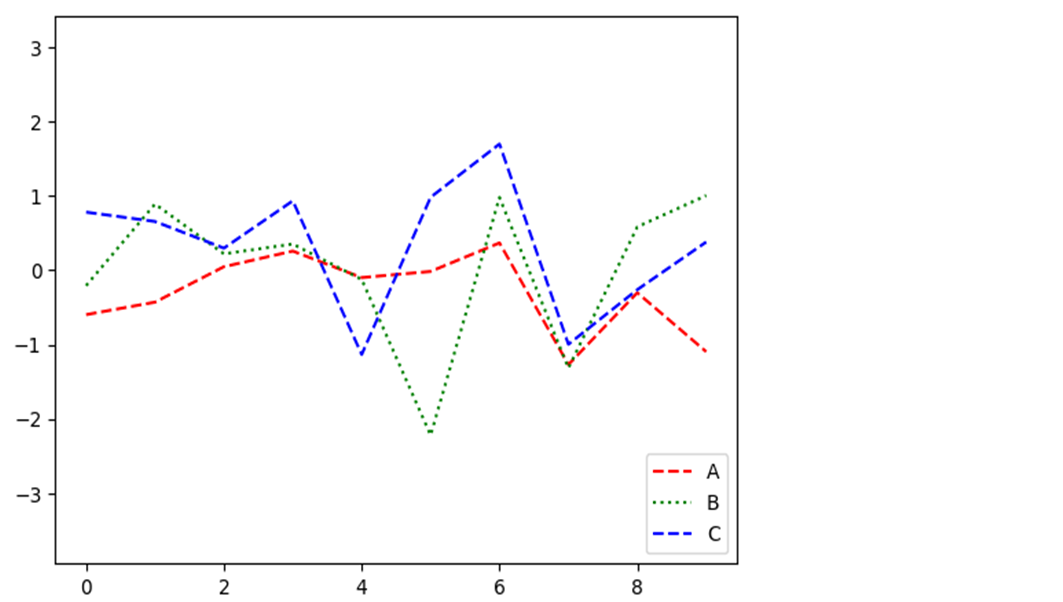
ax.legend(loc='lower right') fig
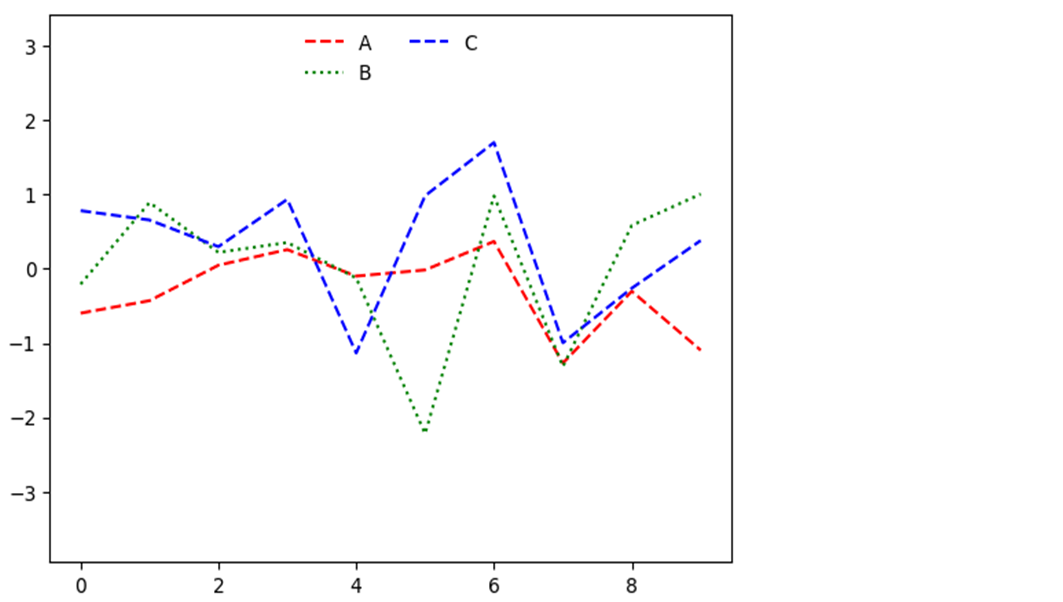
ax.legend(loc='upper center', frameon=False, ncol=2) fig
ax.legend(fancybox=True, framealpha=1, shadow=True, borderpad=1) fig
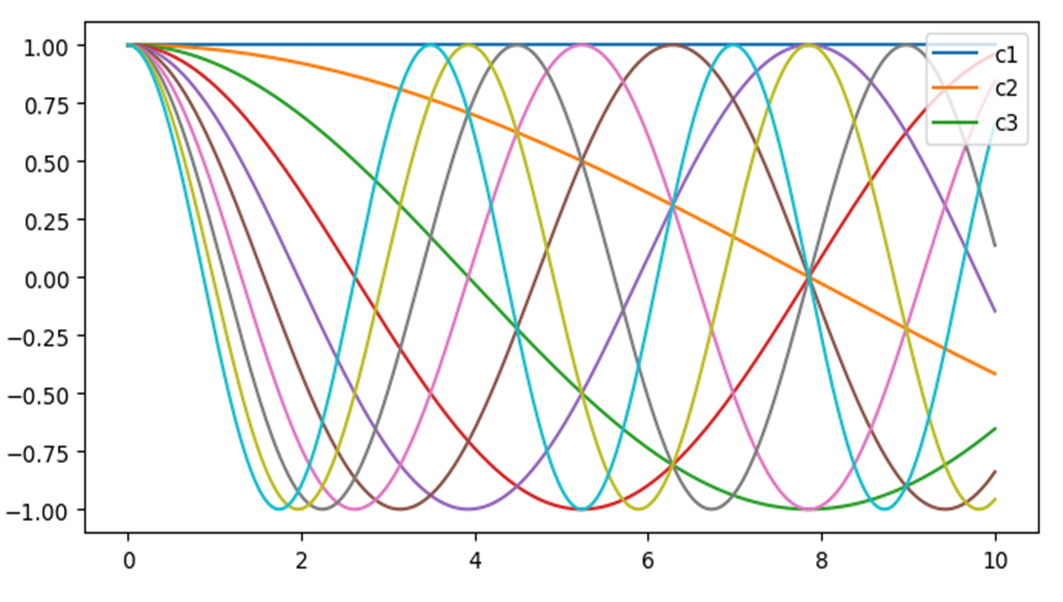
plt.figure(figsize=(8,4)) x = np.linspace(0, 10, 1000) y = np.cos(x[:, np.newaxis]*np.arange(0, 2, 0.2)) lines = plt.plot(x,y) plt.legend(lines[:3], ['c1', 'c2', 'c3', 'c4'], loc='upper right');
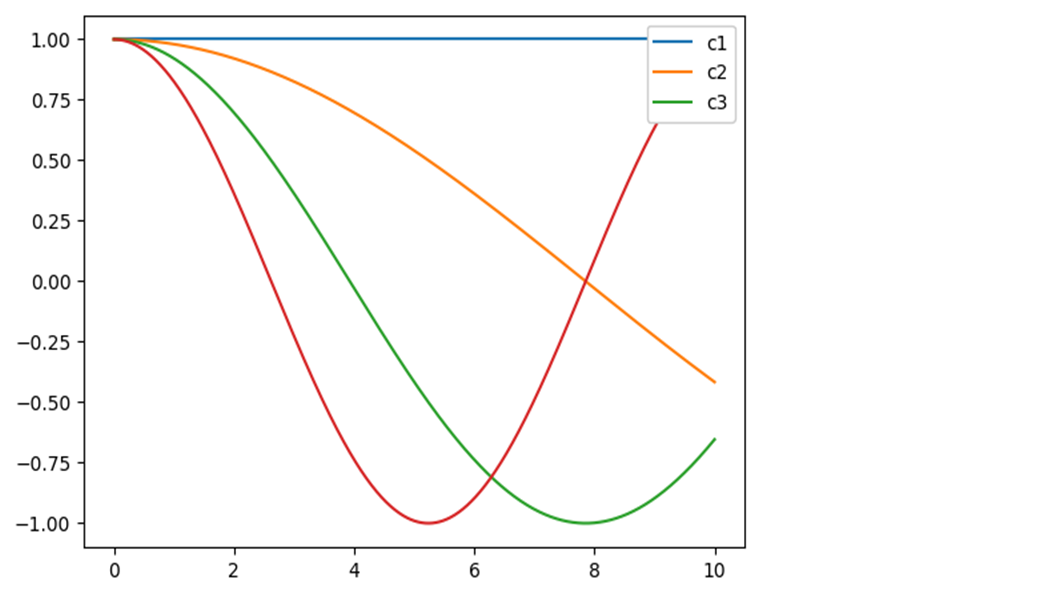
plt.plot(x, y[:,0], label='c1') plt.plot(x, y[:,1], label='c2') plt.plot(x, y[:,2], label='c3') plt.plot(x, y[:,3]) plt.legend(framealpha = 1, frameon=True, loc='upper right');
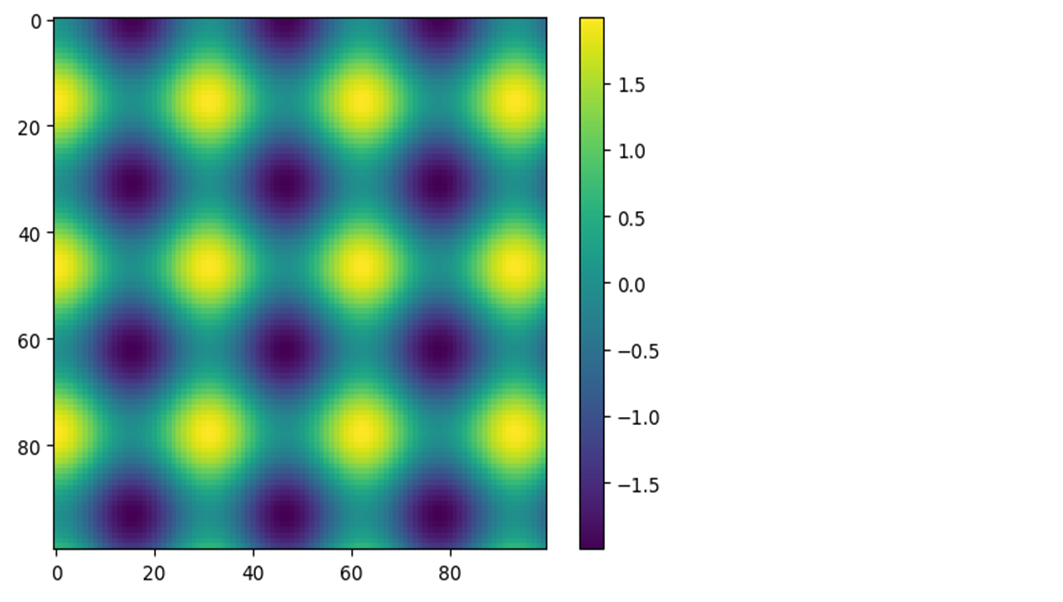
x = np.linspace(0,20,100) I = np.cos(x) - np.cos(x[:, np.newaxis]) plt.imshow(I) plt.colorbar();
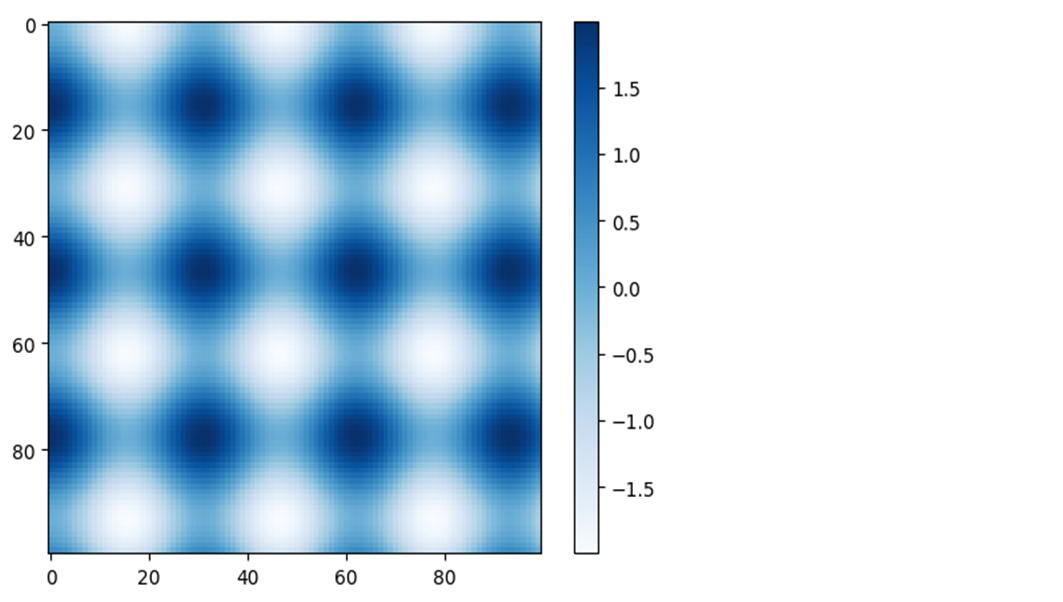
plt.imshow(I, cmap='Blues') plt.colorbar();
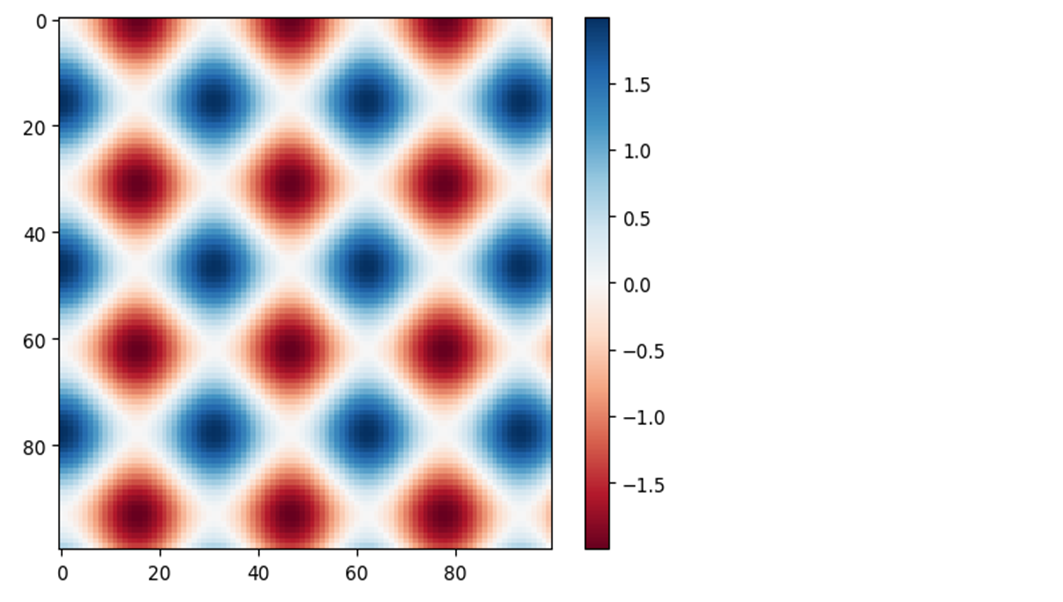
plt.imshow(I, cmap='RdBu') plt.colorbar();
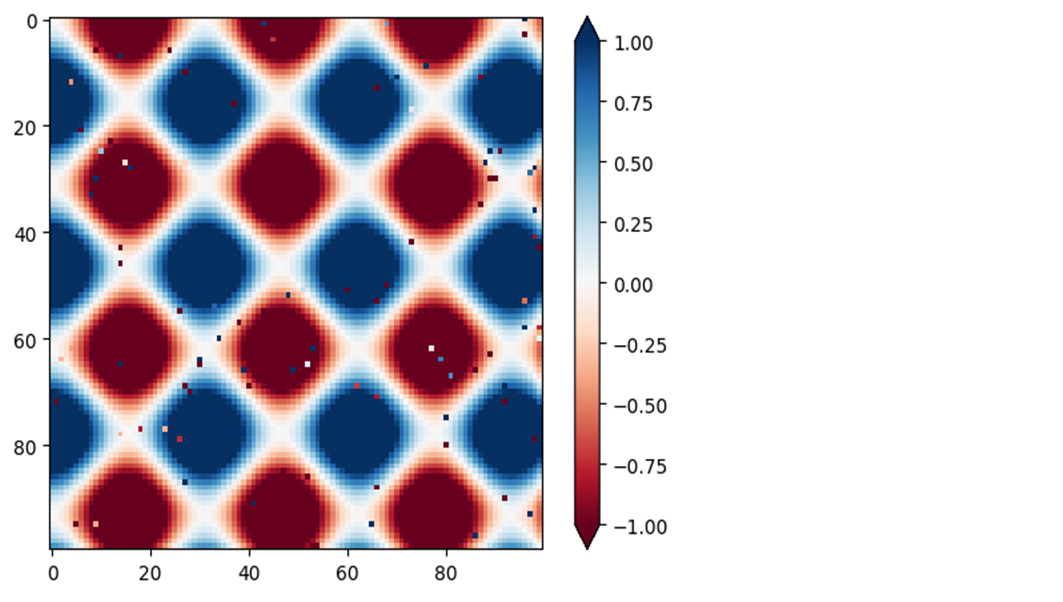
speckles = (np.random.random(I.shape) < 0.01) I[speckles] = np.random.normal(0,3,np.count_nonzero(speckles)) plt.imshow(I, cmap='RdBu') plt.colorbar(extend='both'); plt.clim(-1,1);
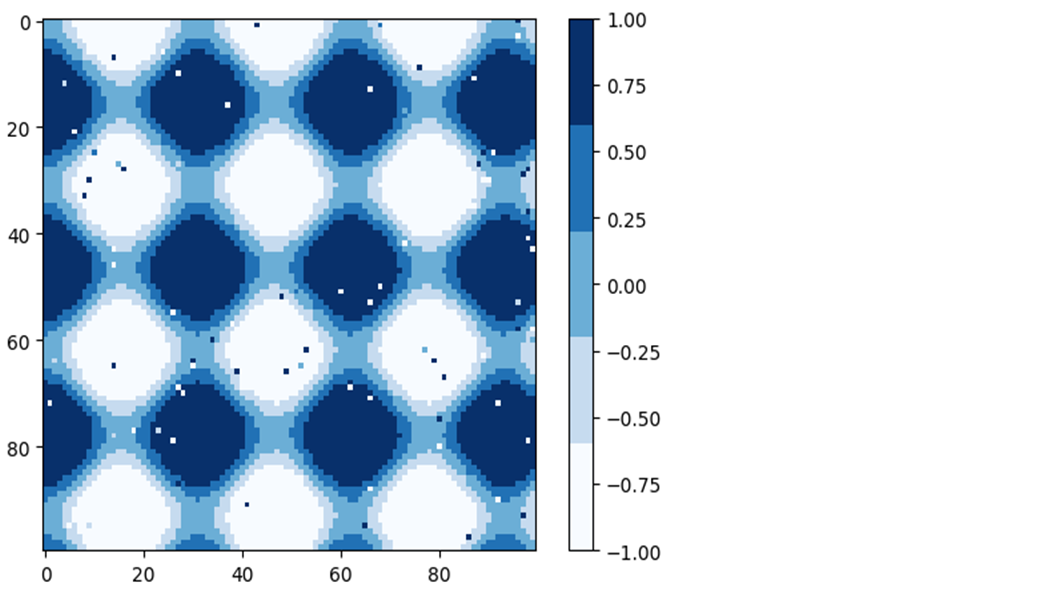
plt.imshow(I, cmap=plt.cm.get_cmap('Blues', 5)) plt.colorbar() plt.clim(-1,1);
다중 플롯(Multiple Subplots)
ax1 = plt.axes() ax2 = plt.axes([0.65, 0.5, 0.2, 0.3])
for i in range(1,10): plt.subplot(3,3,i) plt.text(0.5, 0.5, str((3,3,i)), ha="center")
fig = plt.figure() fig.subplots_adjust(hspace = 0.4, wspace=0.4) for i in range(1,10): plt.subplot(3,3,i) plt.text(0.5, 0.5, str((3,3,i)), ha="center")
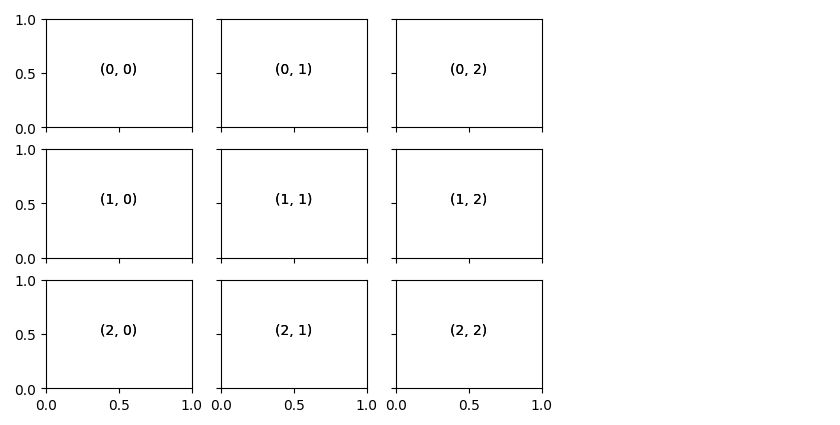
fig, ax=plt.subplots(3,3, sharex='col', sharey='row')
for i in range(3): for j in range(3): ax[i, j].text(0.5, 0.5, str((i, j)), ha="center") fig
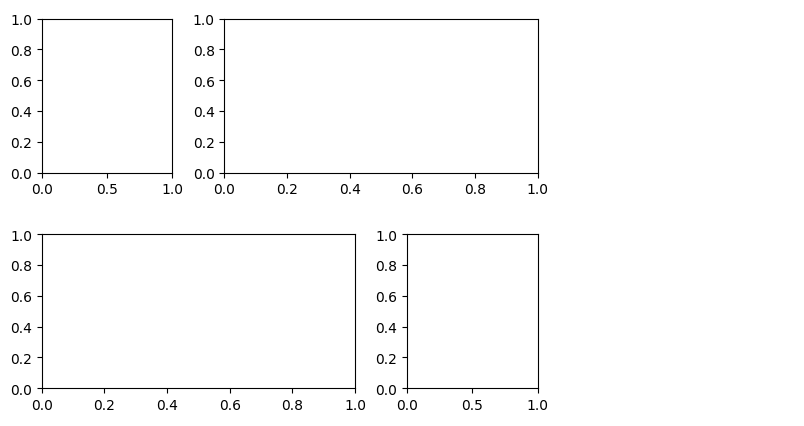
grid = plt.GridSpec(2,3,wspace=0.4, hspace=0.4)plt.subplot(grid[0,0]) plt.subplot(grid[0,1:]) plt.subplot(grid[1,:2]) plt.subplot(grid[1,2])
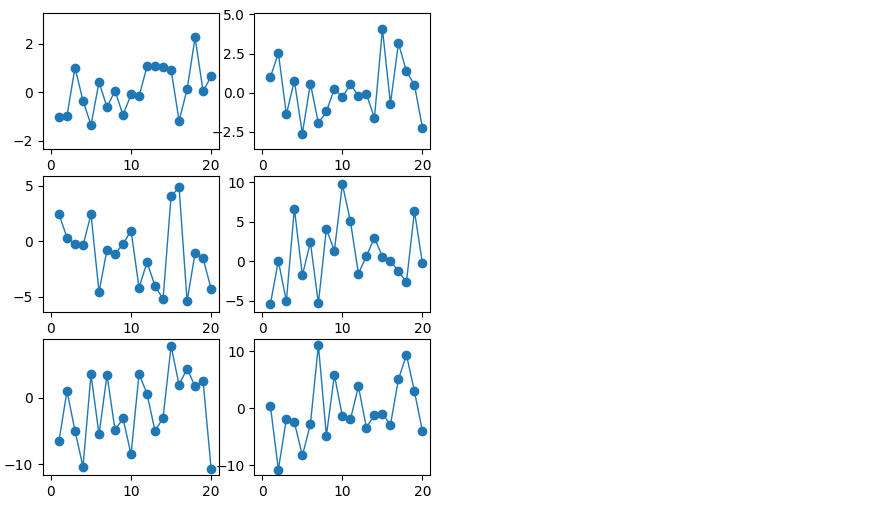
plt.figure(figsize=(5,6))x = range(1,21) columns = [np.random.randn(20) * i for i in range(1,7)]i=0 for c in columns: i += 1plt.subplot(3,2,i) plt.plot(x,c,marker='o', linewidth=1, label=c) plt.xlim(-1,21) plt.ylim(c.min()-1, c.max()+1)
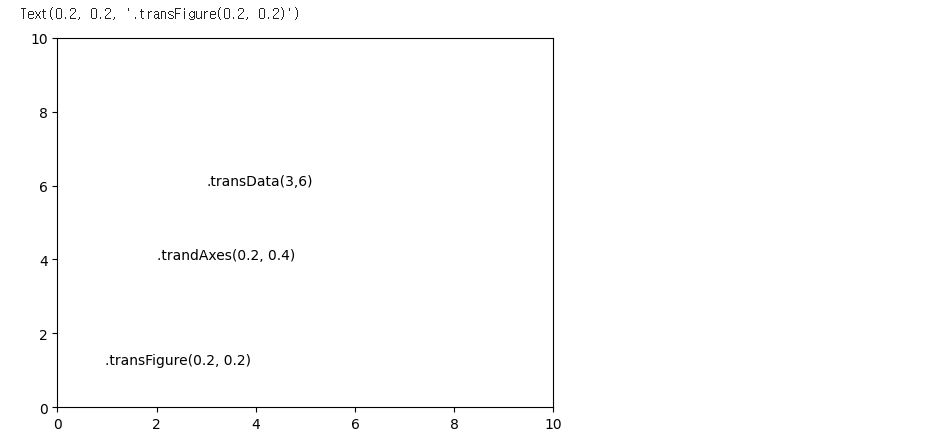
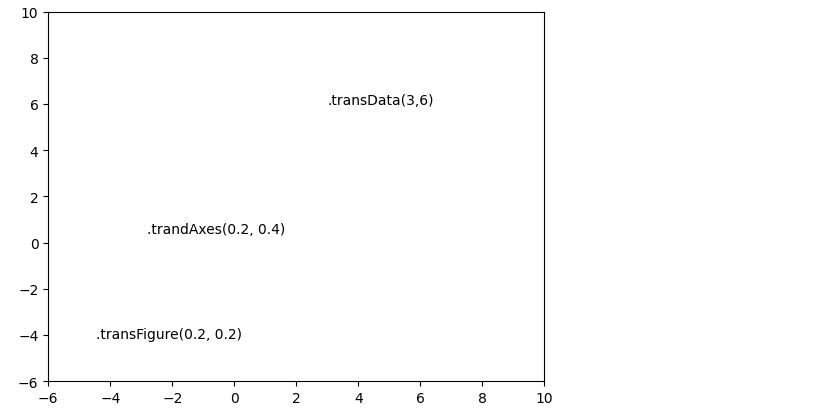
텍스트와 주석(Text and Annotation)
fig, ax = plt.subplots() ax.axis([0,10,0,10]) ax.text(3,6,".transData(3,6)", transform=ax.transData) ax.text(0.2, 0.4, ".trandAxes(0.2, 0.4)", transform = ax.transAxes) ax.text(0.2, 0.2, ".transFigure(0.2, 0.2)", transform = fig.transFigure)
ax.set_xlim(-6,10) ax.set_ylim(-6,10) fig
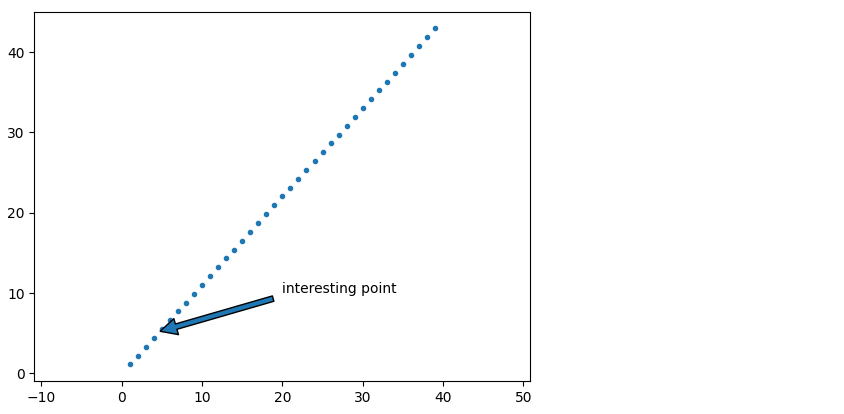
x = np.arange(1,40) y = x * 1.1 plt.scatter(x,y, marker='.') plt.axis('equal') plt.annotate('interesting point', xy=(4, 5), xytext=(20, 10), arrowprops=dict(shrink=0.05))
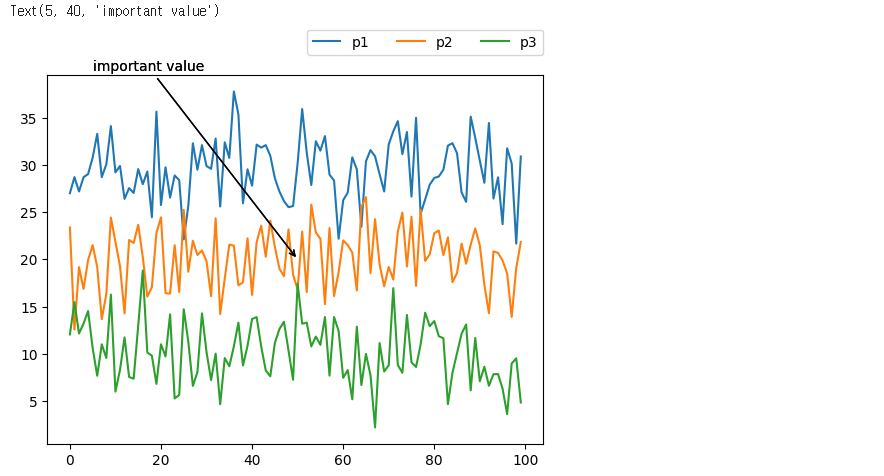
x1 = np.random.normal(30,3,100) x2 = np.random.normal(20,3,100) x3 = np.random.normal(10,3,100)plt.plot(x1, label='p1') plt.plot(x2, label='p2') plt.plot(x3, label='p3')plt.legend(bbox_to_anchor=(0., 1.02, 1., .102), loc=0, ncol=3, mode='extend', borderaxespad=0.) plt.annotate("important value", (50,20), xytext=(5,40), arrowprops = dict(arrowstyle='->')) plt.annotate("important value", (50,20), xytext=(5,40), arrowprops = dict(arrowstyle='->'))
눈금 맞춤(Customizing Ticks)
plt.axes(xscale='log', yscale='log')
ax = plt.axes() ax.plot(np.random.randn(100).cumsum())ax.yaxis.set_major_locator(plt.NullLocator()) ax.xaxis.set_major_formatter(plt.NullFormatter())
fig, ax = plt.subplots(3,3, sharex=True, sharey=True)
for axi in ax.flat: axi.xaxis.set_major_locator(plt.MaxNLocator(4)) axi.yaxis.set_major_locator(plt.MaxNLocator(4)) fig
x = np.linspace(-np.pi, np.pi, 1000, endpoint=True) y = np.sin(x) plt.plot(x,y)ax = plt.gca() ax.spines['bottom'].set_position(('data',0)) ax.spines['left'].set_position(('data',0)) ax.xaxis.set_ticks_position('bottom') ax.yaxis.set_ticks_position('left')
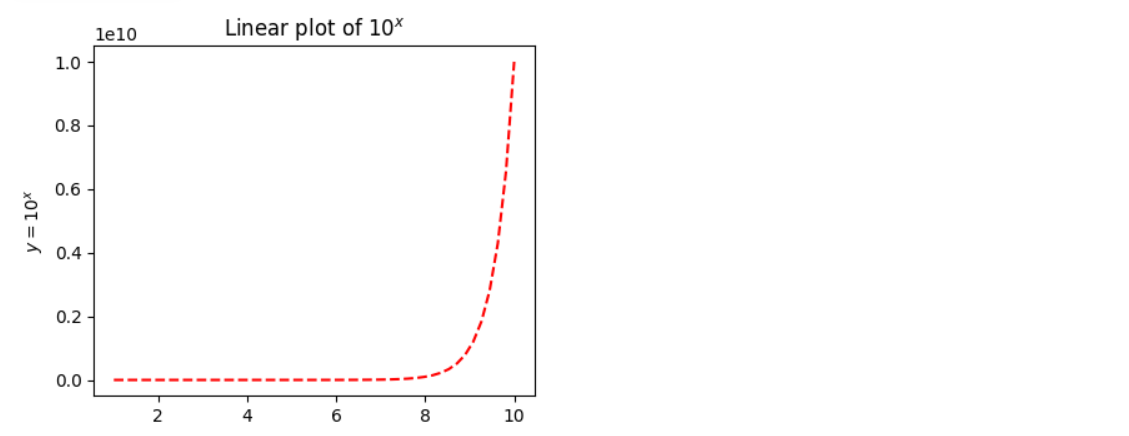
x = np.linspace(1,10) y = [10**el for el in x] z = [2*el for el in x] fig = plt.figure(figsize=(10,8)) # ax1 = fig.add_subplot(2,2,1) ax1.plot(x,y,'--r') ax1.set_yscale('linear') ax1.set_title('Linear plot of $ {10}^{x} $') ax1.set_ylabel(r'${y} = {10}^{x}$') plt.grid(b=True, which='both', axis='both') # ax2 = fig.add_subplot(2,2,2) ax2.plot(x,y,'-.g') ax2.set_yscale('log') ax2.set_title('Logarithmic plot of $ {2}^{x} $') ax2.set_ylabel(r'${y} = {10}^{x}$') plt.grid(b=True, which='both', axis='both') # ax3 = fig.add_subplot(2,2,3) ax3.plot(x,y,':b') ax3.set_yscale('linear') ax3.set_title('Linear plot of $ {10}^{x} $') ax3.set_ylabel(r'${y} = {10}^{x}$') plt.grid(b=True, which='both', axis='both') # ax4 = fig.add_subplot(2,2,4) ax4.plot(x,y,':b') ax4.set_yscale('linear') ax4.set_title('Linear plot of $ {10}^{x} $') ax4.set_ylabel(r'${y} = {2}^{x}$') plt.grid(b=True, which='both', axis='both')
스타일
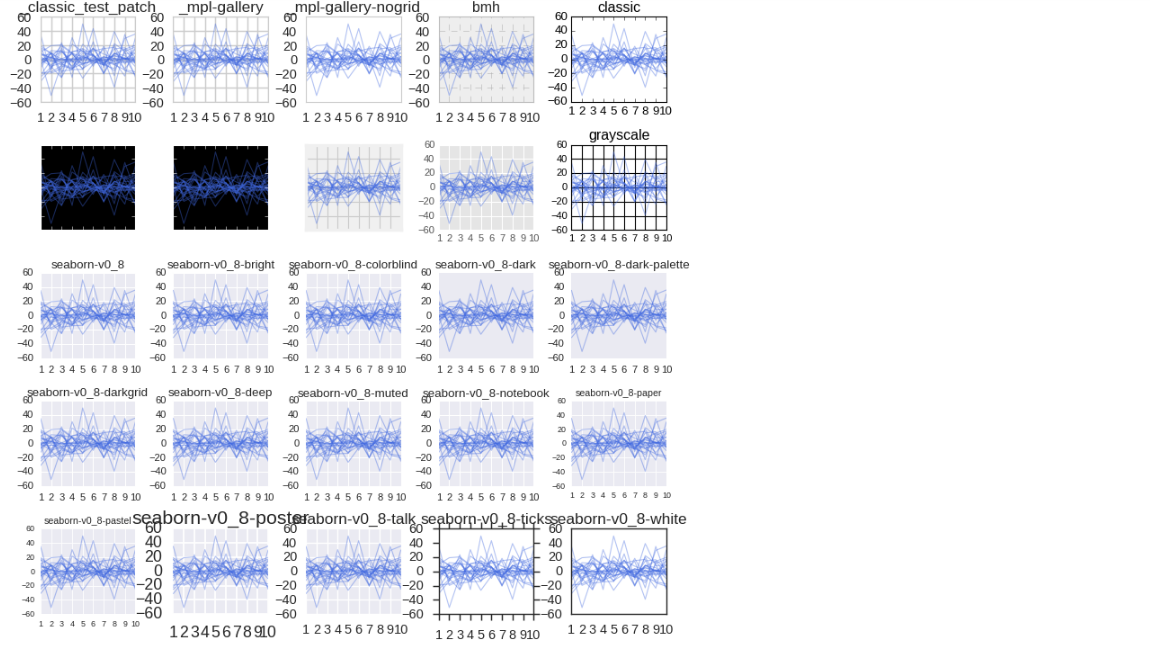
fig = plt.figure(figsize=(10,10)) #ValueError은 나오나 2021년 강의라서 그 때의 버전차이가 있을 거라고 예상된다. 출력은 나온다. x = range(1,11) columns = [np.random.randn(10)*i for i in range(1, 26)] # for n, v in enumerate(plt.style.available[1:]): plt.style.use(v) plt.subplot(5, 5, n+1) plt.title(v) # for c in columns: plt.plot(x, c, marker='', color='royalblue', linewidth=1, alpha=0.4) plt.subplots_adjust(hspace = 0.5, wspace = 0.4)
plt.style.use(['seaborn-notebook']) #<ipython-input-6-16b681008e18>:1: #MatplotlibDeprecationWarning: The seaborn styles shipped #by Matplotlib are deprecated since 3.6, as they no longer #correspond to the styles shipped by seaborn. However, #they will remain available as 'seaborn-v0_8-<style>'. #Alternatively, directly use the seaborn API instead. # plt.style.use(['seaborn-notebook'])
플롯 종류

막대 플롯(Barplot)
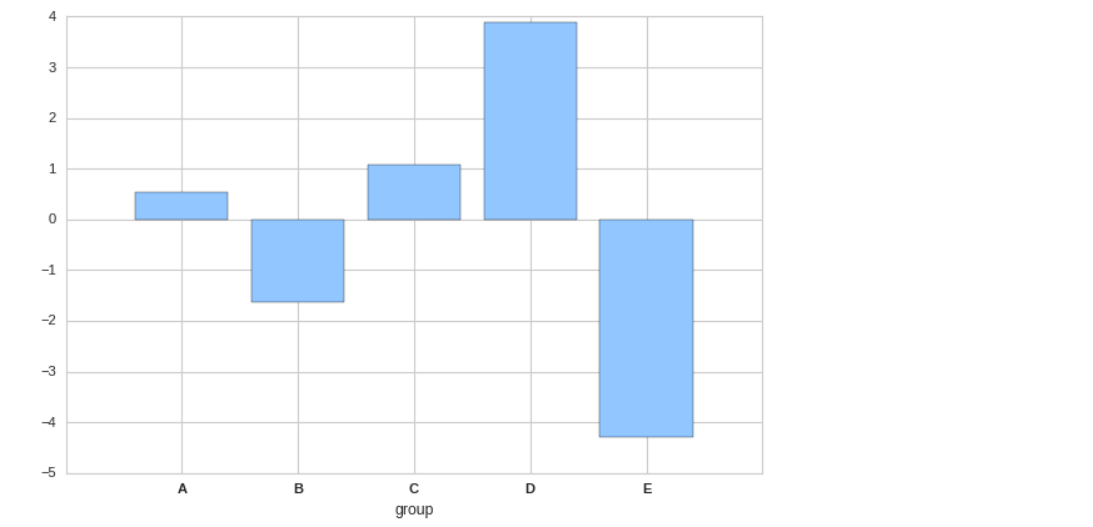
height = [np.random.randn() * i for i in range(1,6)] names = ['A', 'B', 'C', 'D', 'E'] y_pos = np.arange(len(names)) plt.bar(y_pos, height) plt.xticks(y_pos, names, fontweight='bold') plt.xlabel('group');
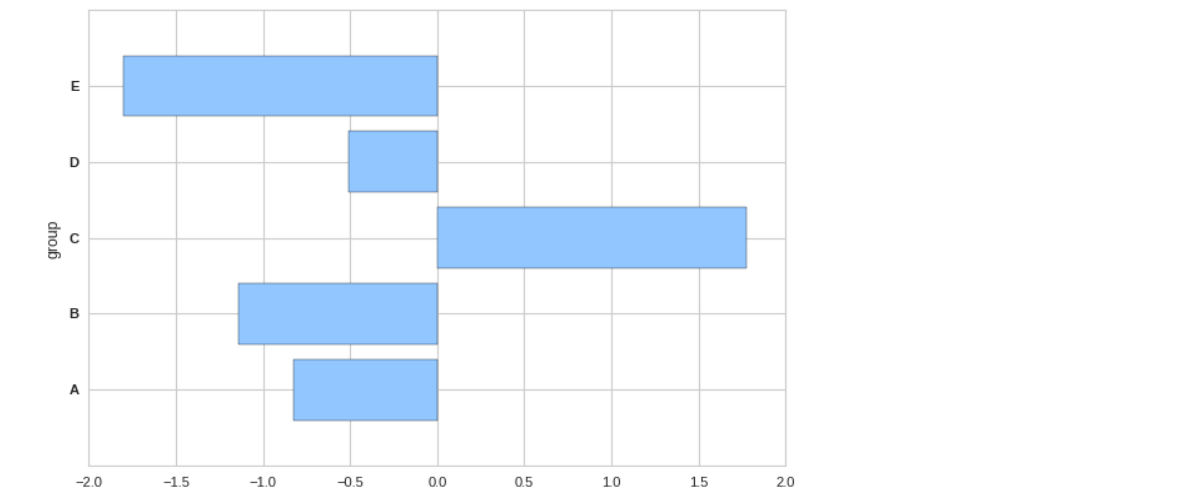
height = [np.random.randn() * i for i in range(1,6)] names = ['A', 'B', 'C', 'D', 'E'] y_pos = np.arange(len(names)) plt.barh(y_pos, height) plt.yticks(y_pos, names, fontweight='bold') plt.ylabel('group');
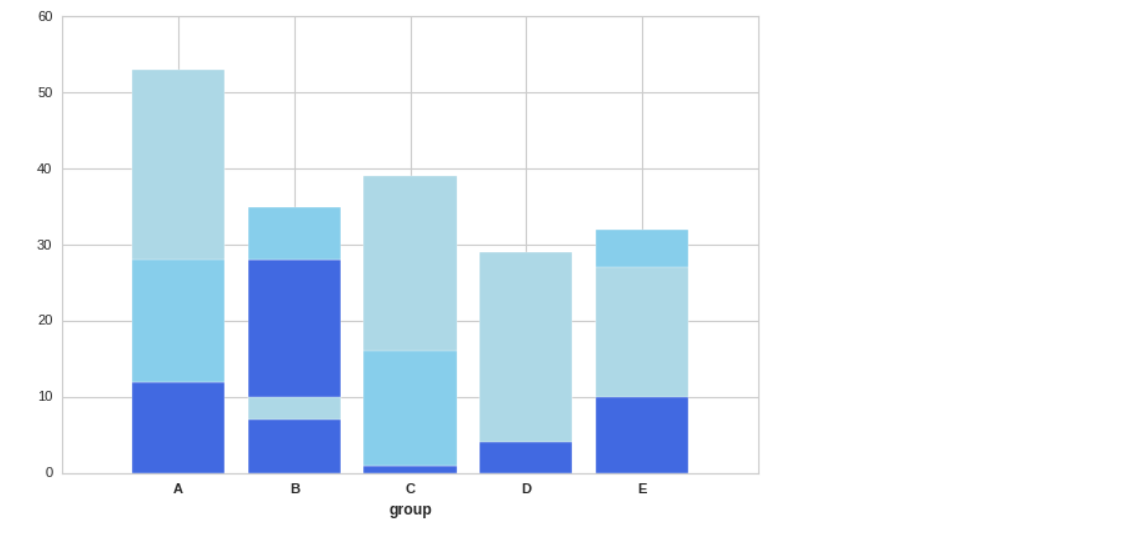
bars1 = [12,28,1,8,22] bars2 = [28,7,16,4,10] bars3 = [25,3,23,25,17] bars = np.add(bars1, bars2).tolist() # r = [0,1,2,3,4] names = ['A', 'B', 'C', 'D', 'E'] # plt.bar(r, bars1, color='royalblue', edgecolor='white') plt.bar(r, bars2, bottom=bars1, color='skyblue', edgecolor='white') plt.bar(r, bars3, bottom=bars2, color='lightblue', edgecolor='white') # plt.xlabel('group', fontweight='bold') plt.xticks(r, names, fontweight='bold')
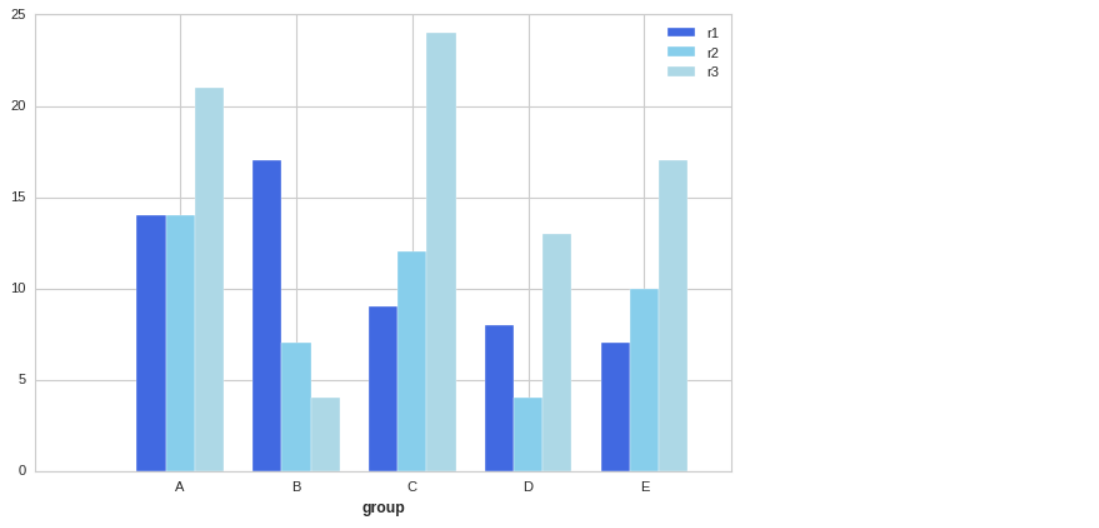
bar_width = 0.25 # bars1 = [14, 17, 9, 8, 7] bars2 = [14, 7, 12, 4, 10] bars3 = [21, 4, 24, 13, 17] # # r1 = np.arange(len(bars1)) r2 = [x + bar_width for x in r1] r3 = [x + bar_width for x in r2] # plt.bar(r1, bars1, color='royalblue', width=bar_width, edgecolor='white', label='r1') plt.bar(r2, bars2, color='skyblue', width=bar_width, edgecolor='white', label='r2') plt.bar(r3, bars3, color='lightblue', width=bar_width, edgecolor='white',label='r3') # plt.xlabel('group', fontweight='bold') plt.xticks([r + bar_width for r in range(len(bars1))], ['A', 'B', 'C', 'D', 'E']) plt.legend();
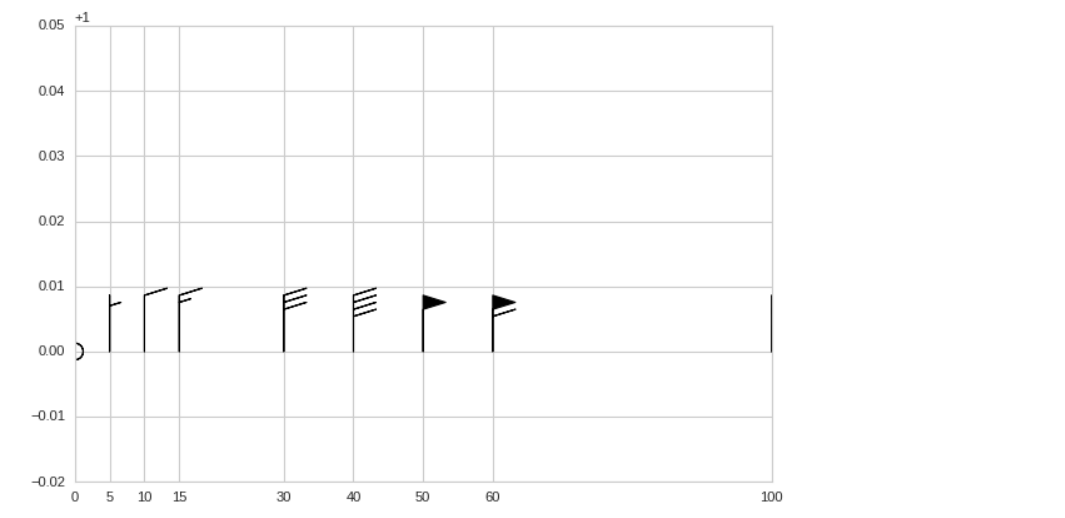
x = [0, 5, 10, 15, 30, 40, 50, 60, 100] v = [0, -5, -10, -15, -30, -40, -50, -60, -100] n = len(v) y = np.ones(n) u = np.zeros(n) # plt.barbs(x, y, u, v, length=9) plt.xticks(x) plt.ylim(0.98, 1.05);
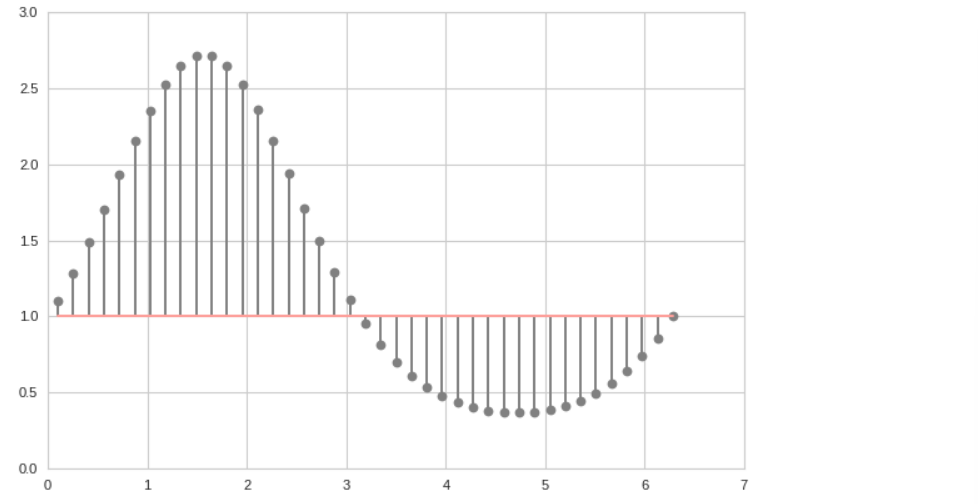
스탬 플롯(Stem Plot)
x = np.linspace(0.1, 2*np.pi, 41) y = np.exp(np.sin(x)) # plt.stem(x, y, linefmt='gray', bottom=1, use_line_collection=True);
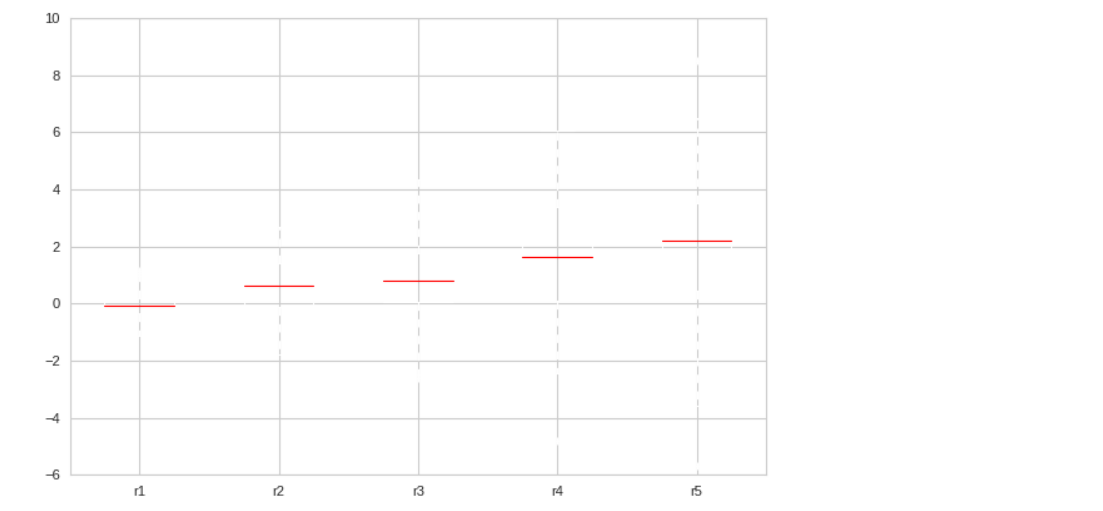
박스플롯(Box Plot)
r1 = np.random.normal(loc = 0, scale=0.5, size=100) r2 = np.random.normal(loc = 0.5, scale=1, size=100) r3 = np.random.normal(loc = 1, scale=1.5, size=100) r4 = np.random.normal(loc = 1.5, scale=2, size=100) r5 = np.random.normal(loc=2, scale=2.5, size=100) # f, ax = plt.subplots(1,1) ax.boxplot((r1, r2, r3, r4, r5)) ax.set_xticklabels(['r1', 'r2', 'r3', 'r4', 'r5']);
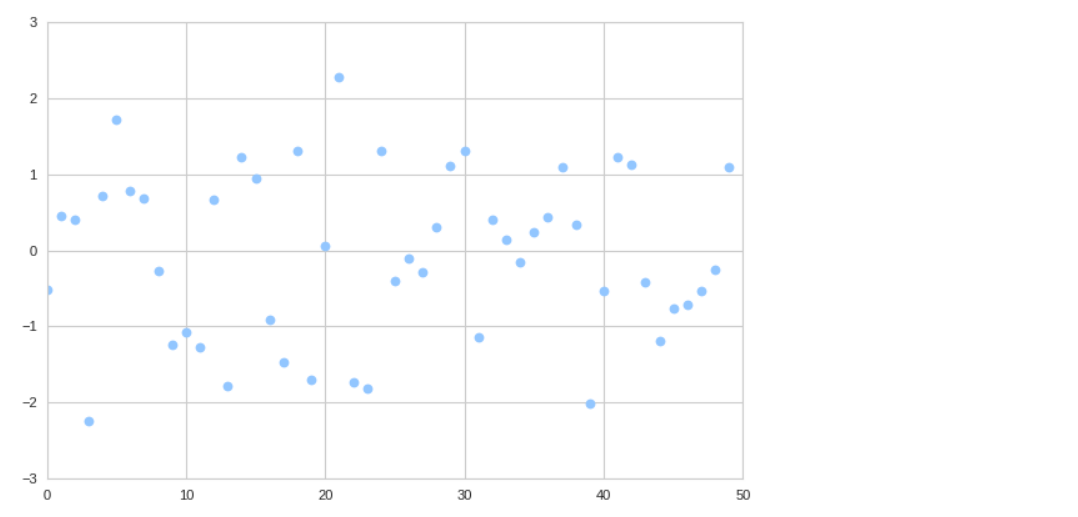
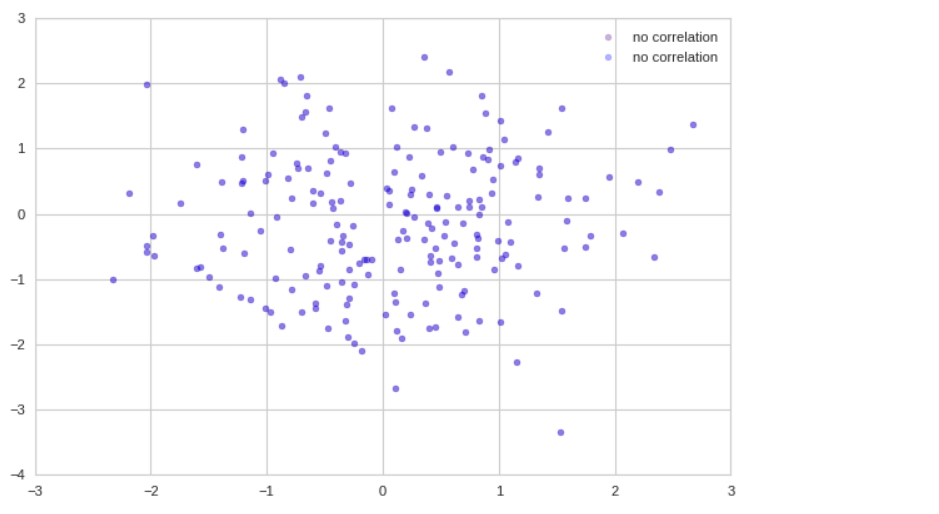
산점도(Scatter Plot)
plt.plot(np.random.randn(50), 'o');
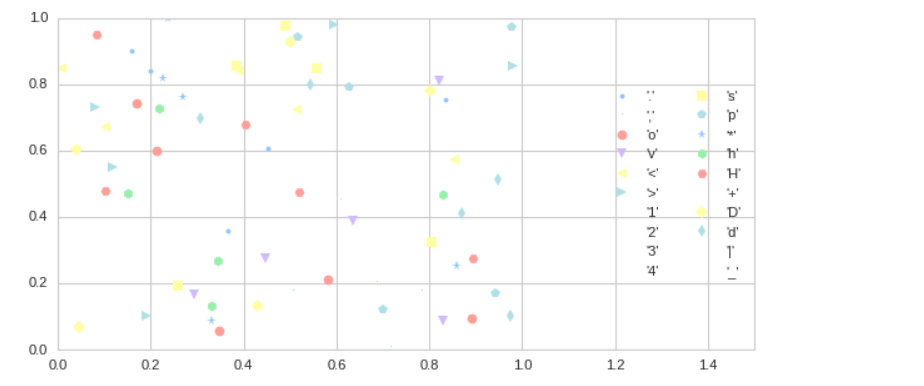
plt.figure(figsize = (8,4)) markers = ['.', ',', 'o', 'v', '<', '>', '1', '2', '3', '4', 's', 'p', '*', 'h', 'H', '+', 'D', 'd', '|', '_'] for m in markers: plt.plot(np.random.rand(5), np.random.rand(5), m, label="'{0}'".format(m)) plt.legend(loc='center right', ncol=2) plt.xlim(0,1.5);
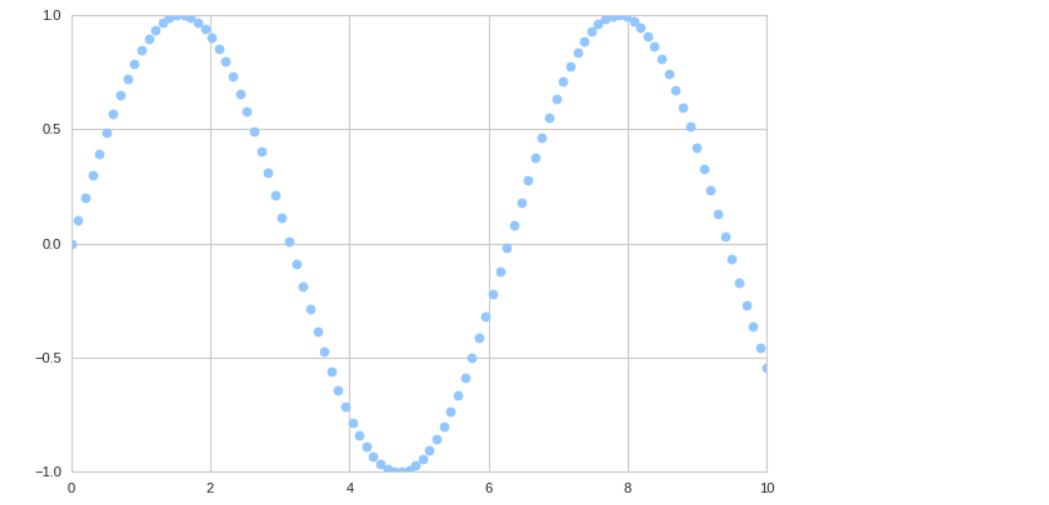
x = np.linspace(0,10,100) y = np.sin(x) # plt.plot(x,y,'o');
plt.scatter(x,y,marker='o');
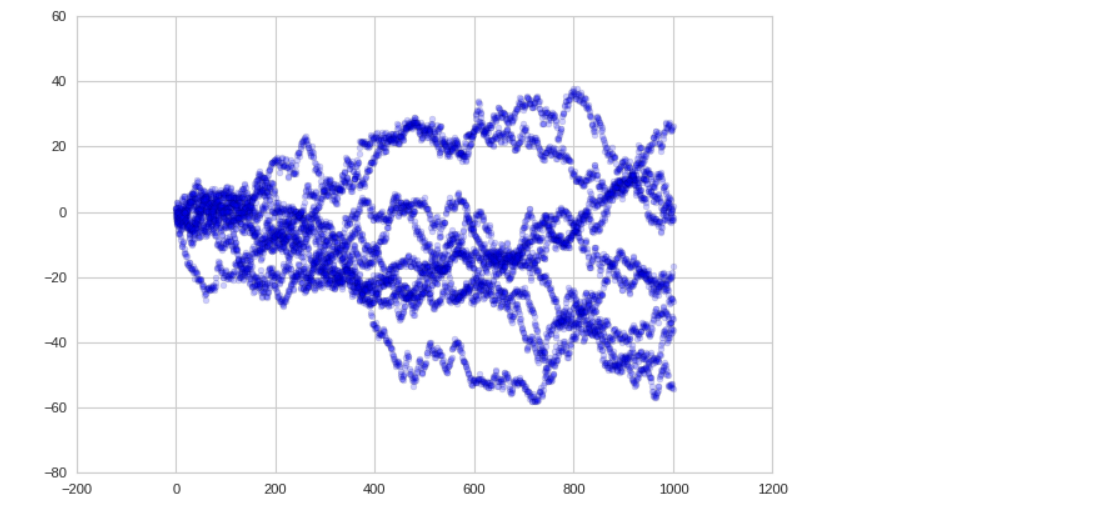
for i in range(9): x = np.arange(1000) y = np.random.randn(1000).cumsum() plt.scatter(x,y,alpha=0.2, cmap = 'viridis')
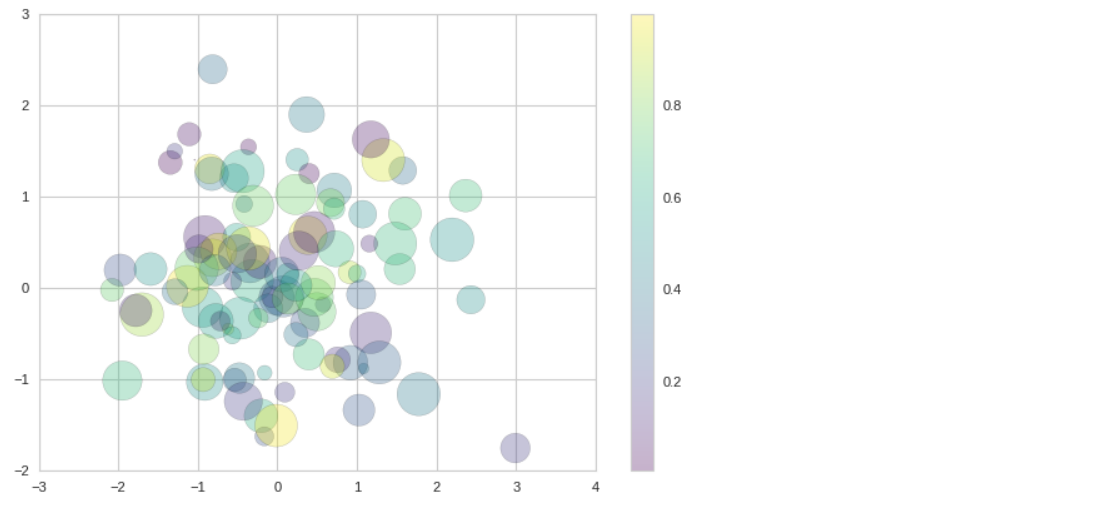
x = np.random.randn(100) y = np.random.randn(100) colors = np.random.rand(100) sizes = 1000 * np.random.rand(100) # plt.scatter(x, y, c=colors, s=sizes, alpha=0.3, cmap="viridis") plt.colorbar();
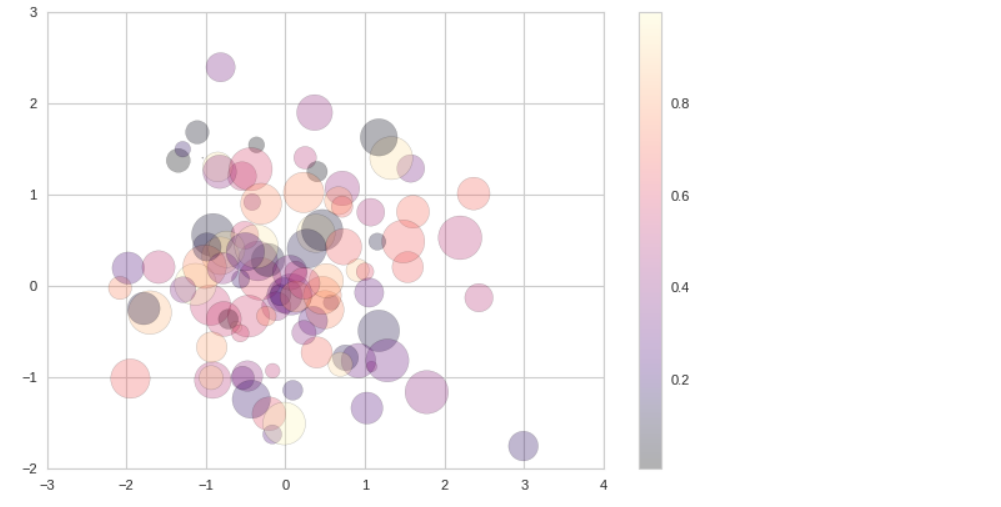
plt.scatter(x, y, c=colors, s=sizes, alpha=0.3, cmap="magma") plt.colorbar();
x = np.random.randn(200) y1 = np.random.randn(len(x)) y2 = 1.1 * np.exp(x) # ax1 = plt.plot() plt.scatter(x,y1,color="indigo", alpha=0.3, label='no correlation') plt.scatter(x,y1,color="blue", alpha=0.3, label='no correlation') plt.grid(True) plt.legend();
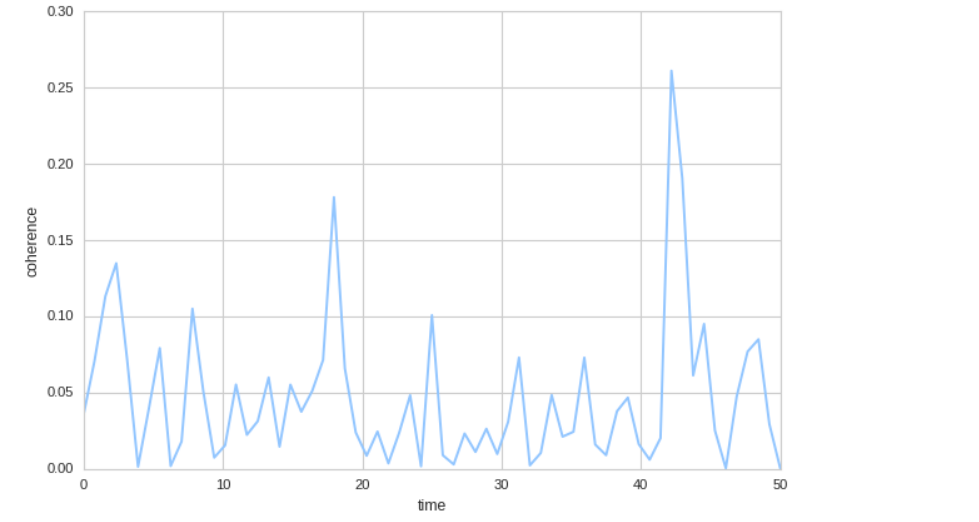
x와 y의 일관성 차트(coherence)
dt = 0.01 t = np.arange(0,30,0.01) n1 = np.random.randn(len(t)) n2 = np.random.randn(len(t)) # s1 = 1.5 * np.sin(2 * np.pi * 10 * t) + n1 s2 = np.cos(np.pi * t) + n2 # plt.cohere(s1, s2**2, 128, 1./dt) plt.xlabel('time') plt.ylabel('coherence')
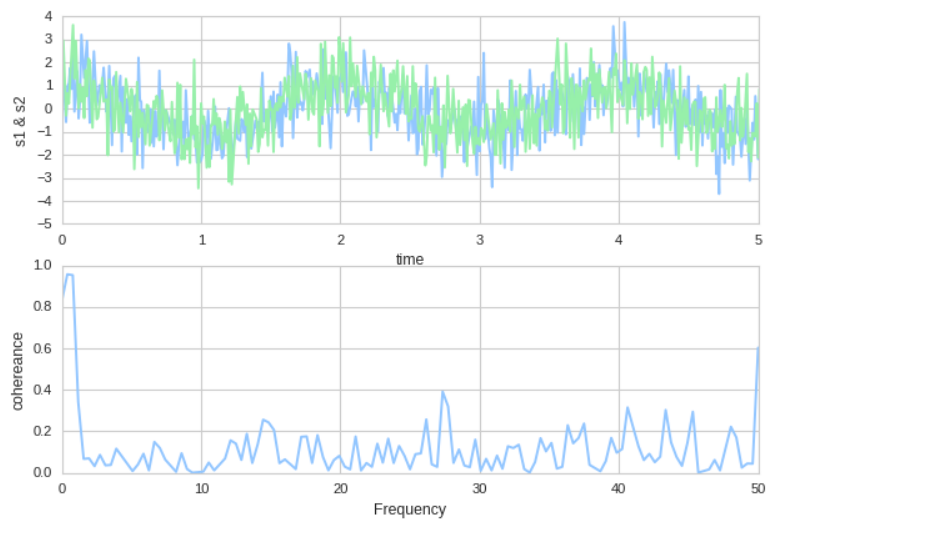
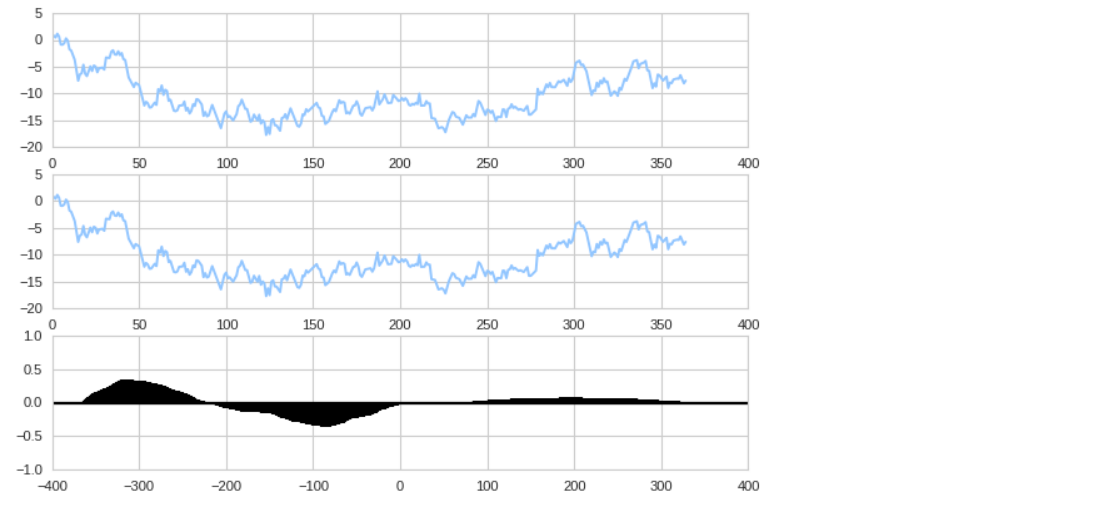
plt.subplots_adjust(wspace=1) # dt = 0.01 t = np.arange(0,30,dt) n1 = np.random.randn(len(t)) n2 = np.random.randn(len(t)) r = np.exp(-t/0.05) # c1 = 1.5 * np.sin(2 * np.pi * 10 * t) + n1 c2 = np.cos(np.pi * t) + n2 # s1 = 0.01 * np.sin(2 * np.pi * 10 * t) + c1 s1 = 0.01 * np.sin(2 * np.pi * 10 * t) + c2 # plt.subplot(211) plt.plot(t, s1, t, s2) plt.xlim(0, 5) plt.xlabel('time') plt.ylabel('s1 & s2') plt.grid(True) # plt.subplot(212) plt.cohere(s1, s2, 256, 1./dt) plt.ylabel('cohereance');
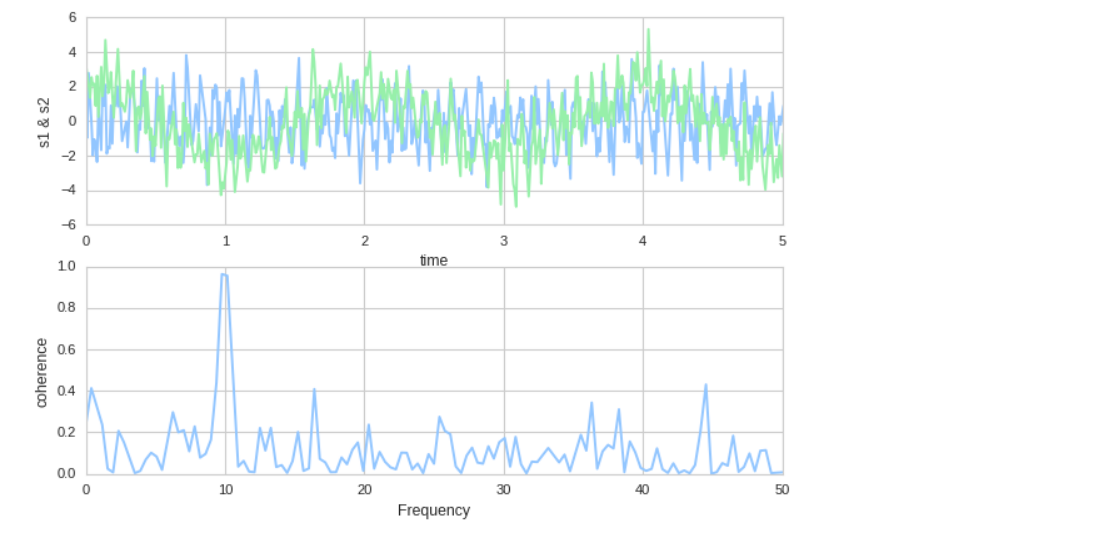
s1 = 0.01 * np.sin(2 * np.pi * 10 * t) + c1 s2 = np.cos(np.pi * t) + c2 + np.sin(2 * np.pi * 10 * t) # fig, [ax1, ax2] = plt.subplots(2,1) ax1.plot(t, s1, t, s2) ax1.set_xlim(0,5) ax1.set_xlabel('time') ax1.set_ylabel('s1 & s2') ax1.grid(True) # ax2.cohere(s1, s2, 256, 1./dt) ax2.set_ylabel('coherence');
d1 = np.random.randn(365).cumsum() t1 = sum(d1) av1 = t1/len(d1) z1 = [i - av1 for i in d1] # d2 = np.random.rand(365).cumsum() t2 = sum(d2) av2 = t2/len(d2) z2 = [i - av1 for i in d2] # fig = plt.figure() # ax1 = fig.add_subplot(311) ax1.plot(d1) # ax2 = fig.add_subplot(312) ax2.plot(d1) # ax3 = fig.add_subplot(313) ax3.xcorr(z1, z2, usevlines=True, maxlags=None, normed=True, lw=2) # # plt.ylim(-1,1);
오차 막대(Error Bar)
- 예상 측정 오차를 나타내는 데 사용
- 오차 막대는 값의 불확실성을 나타냄
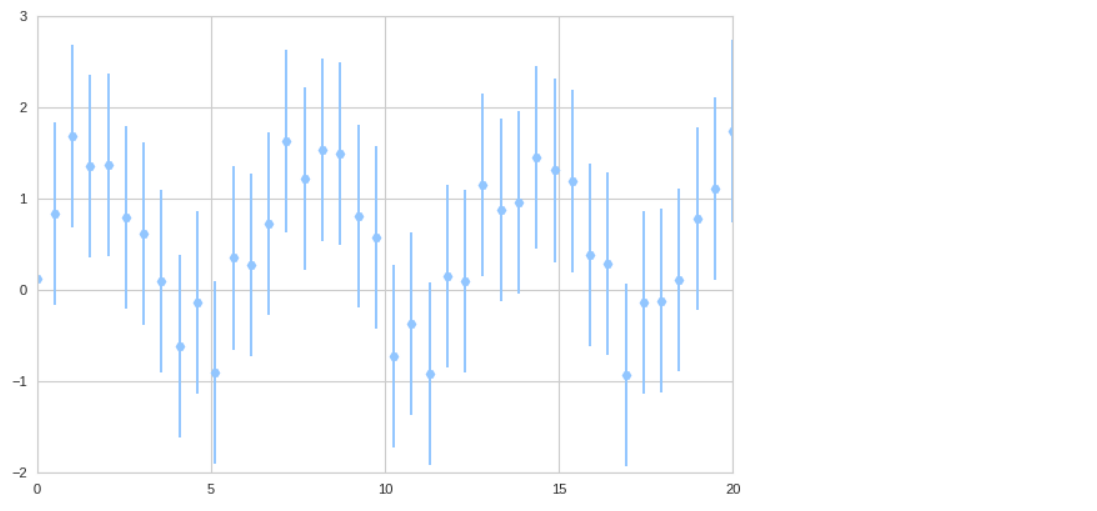
x = np.linspace(0,20,40) dy =1 y = np.sin(x) + dy * np.random.rand(40) # plt.errorbar(x,y,yerr=dy, fmt='H')
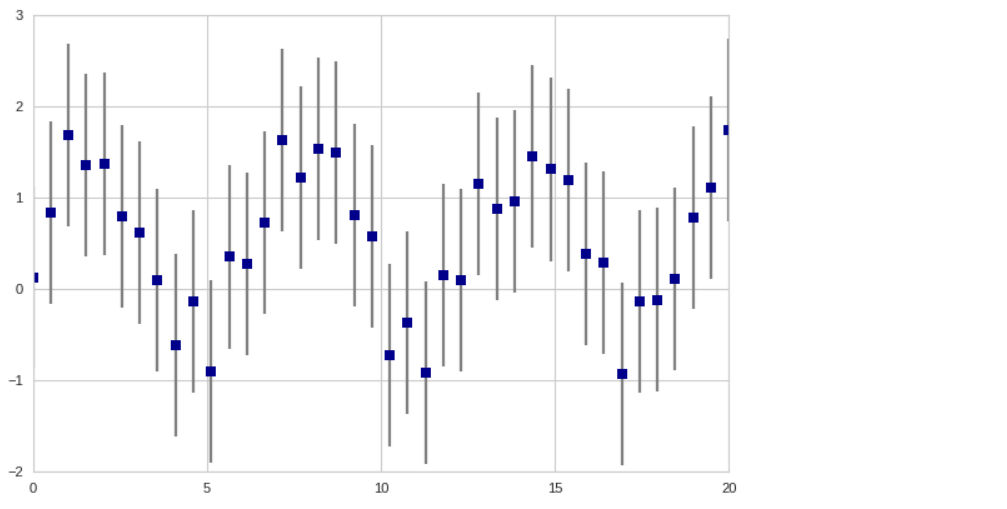
plt.errorbar(x,y,yerr=dy, fmt='s', color='darkblue', ecolor='gray', elinewidth=2, capsize=0);
2차원 유사 플롯(pcolor/pcolormesh)
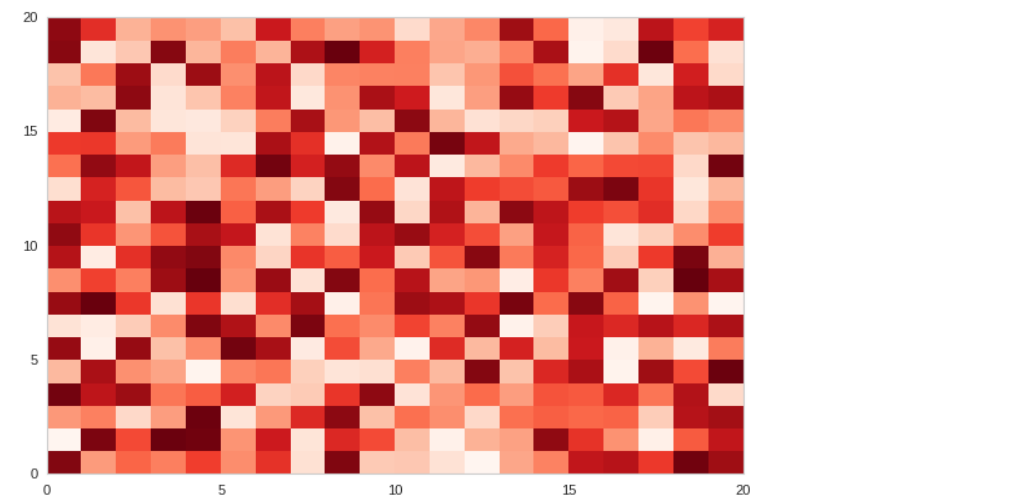
plt.pcolor(np.random.rand(20,20), cmap='Reds');
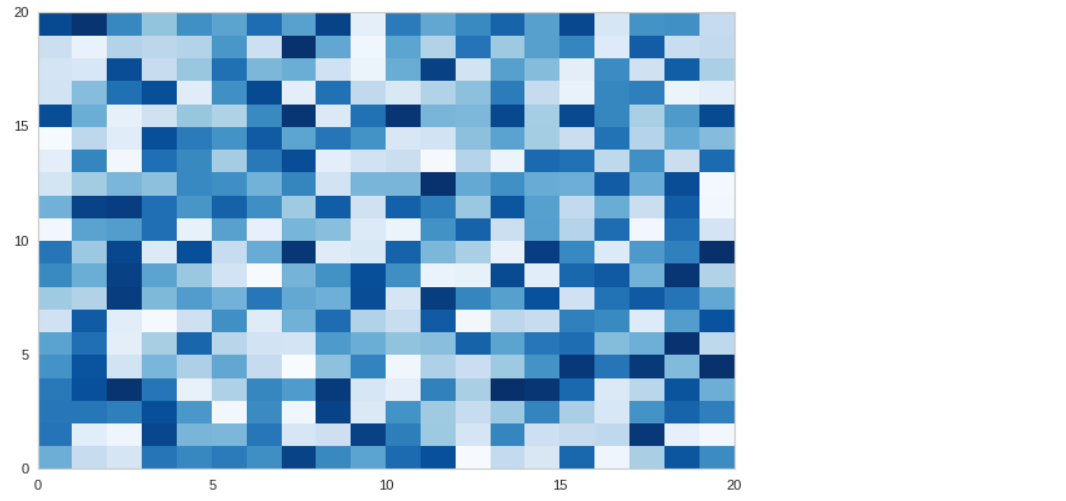
plt.pcolor(np.random.rand(20,20), cmap='Blues');
히스토그램, 구간화, 밀도(Histogram, Binnings, and Density)
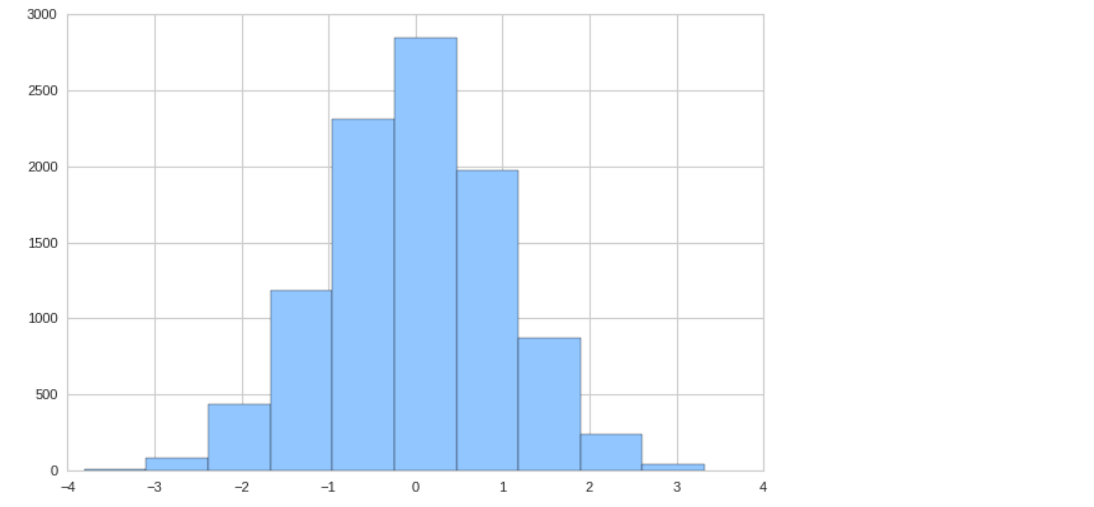
data = np.random.randn(10000) plt.hist(data);
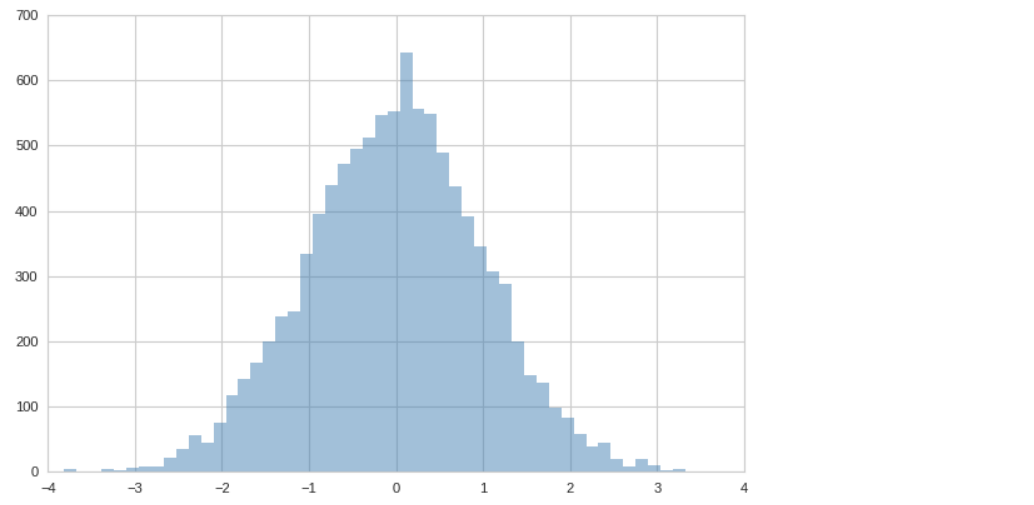
plt.hist(data, bins=50, alpha=0.5, histtype='stepfilled', color='steelblue', edgecolor='none');
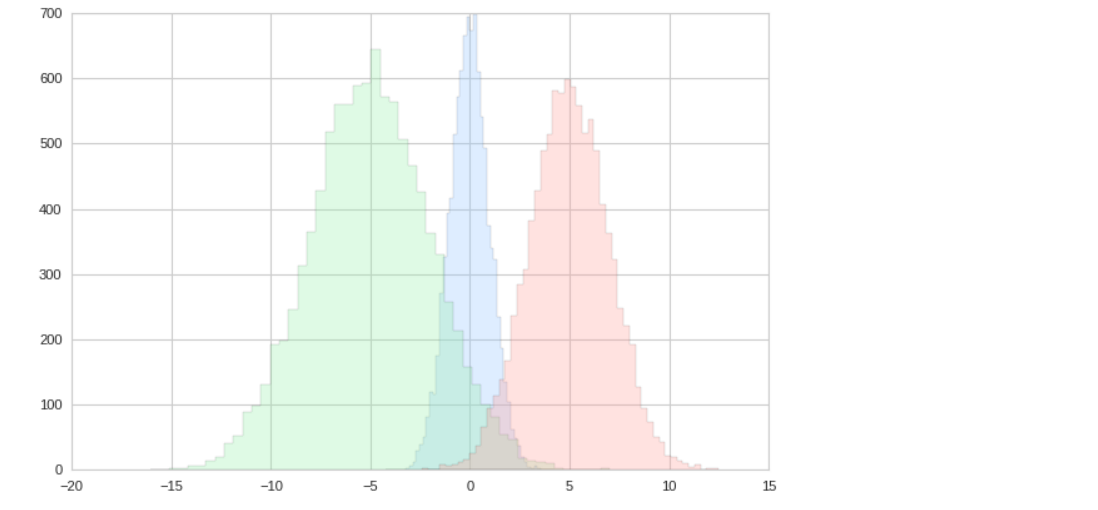
x1 = np.random.normal(0,1,10000) x2 = np.random.normal(-5,3,10000) x3 = np.random.normal(5,2,10000) d = dict(histtype="stepfilled", alpha=0.3, bins=50) # plt.hist(x1, **d) plt.hist(x2, **d) plt.hist(x3, **d)
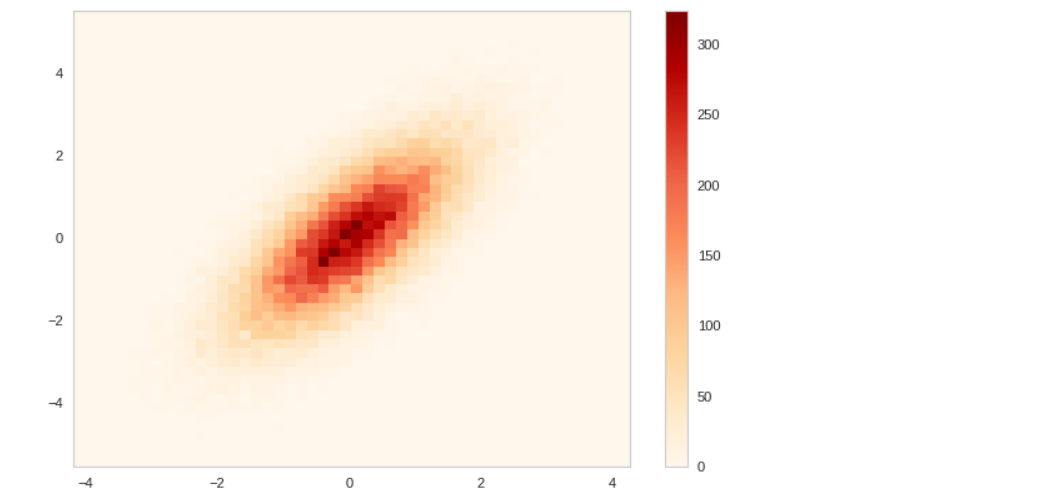
x = np.random.normal(size = 50000) y = x - np.random.normal(size = 50000) # plt.hist2d(x,y, bins=50, cmap='OrRd') plt.colorbar();
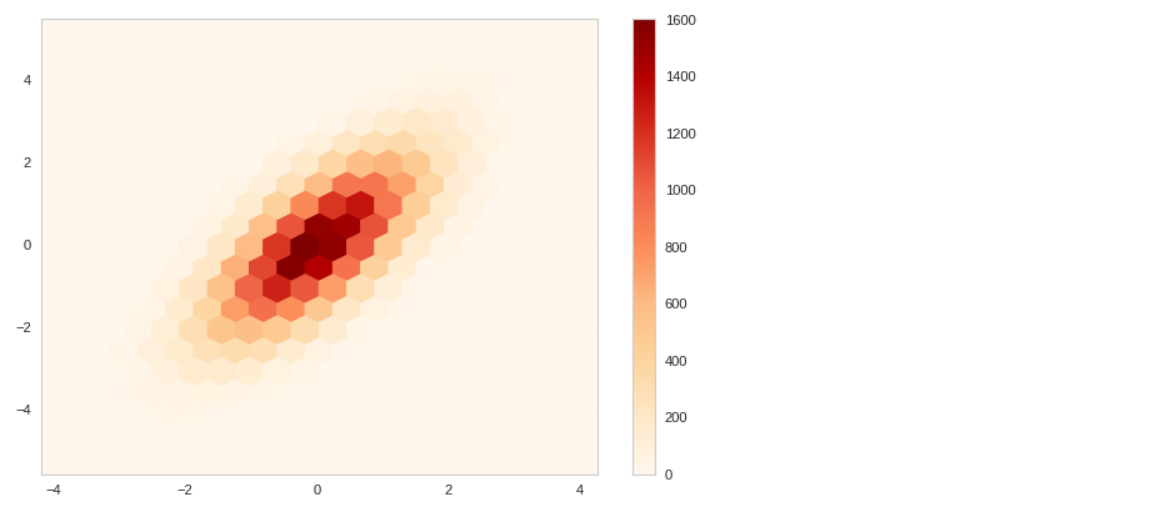
plt.hexbin(x,y, gridsize=20, cmap='OrRd') plt.colorbar();
밀도와 등고선 플롯(Density and Contour Plots)
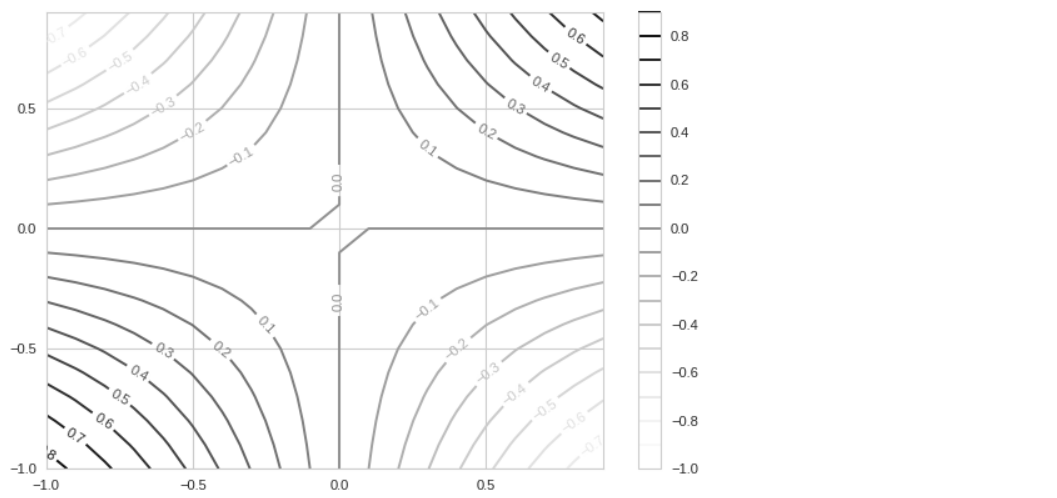
a = np.arange(-1,1,0.1) X, Y = np.meshgrid(a,a) Z = np.sin(X * Y) CS = plt.contour(X, Y, Z, levels=a) plt.clabel(CS, inline=2) plt.colorbar();
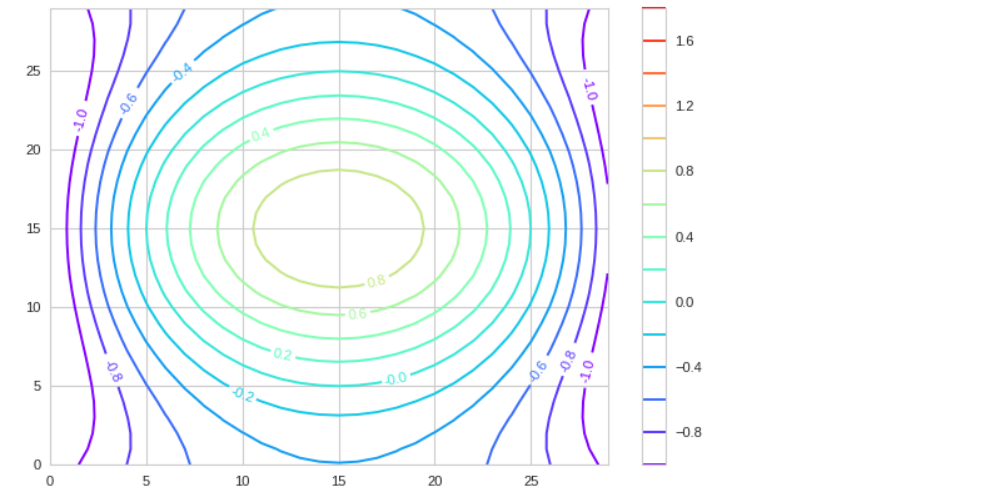
def f(x,y): return (1 - (x**2 + y**2)) * np.exp(-y ** 2 /2) # x = np.arange(-1.5, 1.5, 0.1) y = np.arange(-1.5, 1.5, 0.1) # X, Y = np.meshgrid(x,y) Z = f(X,Y) N = np.arange(-1, 2, 0.2) # CS = plt.contour(Z, N, linewidth=2, cmap='rainbow') plt.clabel(CS, inline=True, fmt='%1.1f') plt.colorbar(CS);
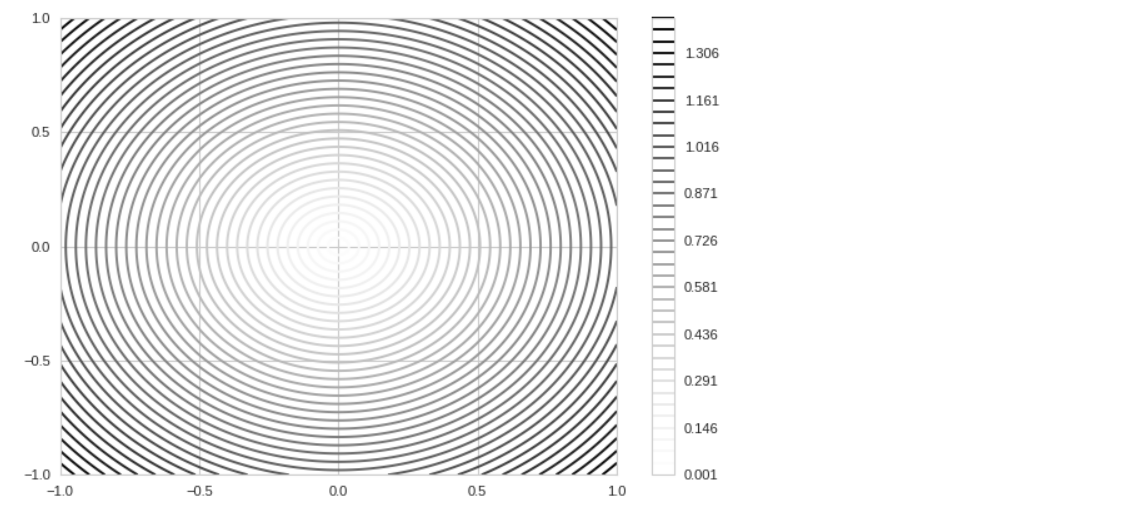
l = np.linspace(-1.0, 1.0, 1000) X,Y = np.meshgrid(l,l) Z = np.sqrt(X ** 2 + Y ** 2) lv = np.linspace(Z.reshape(-1,1).min(), Z.reshape(-1,1).max(), 40) plt.contour(X, Y, Z, levels=lv) plt.colorbar();
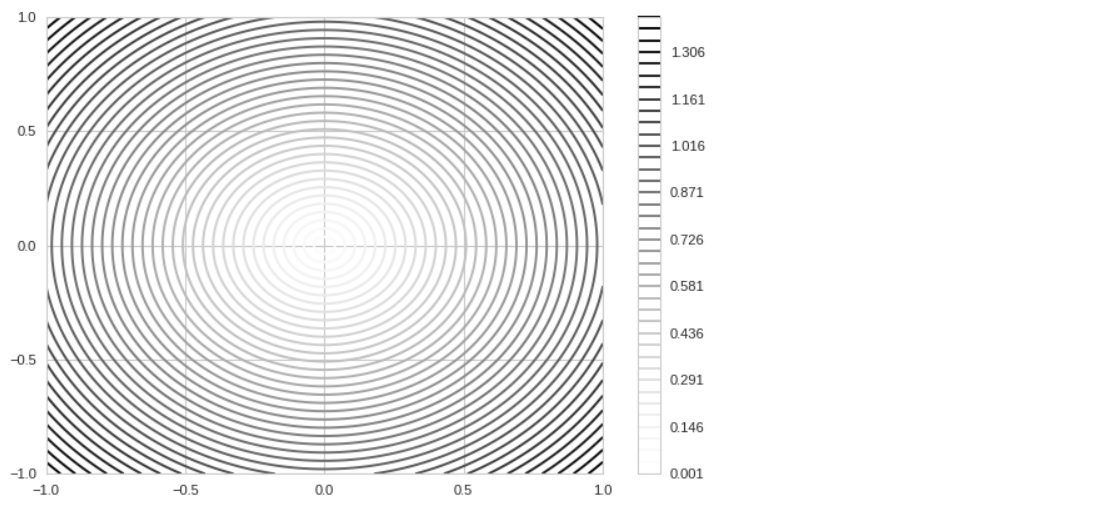
plt.contour(X, Y, Z, levels=lv) plt.colorbar();
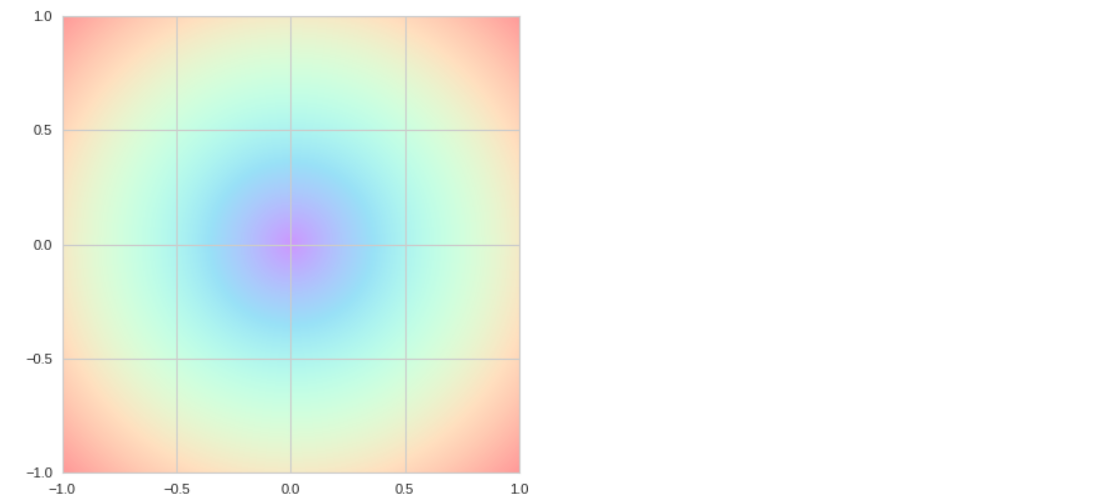
plt.imshow(Z, extent=[-1,1,-1,1], origin='lower', cmap='rainbow', alpha=0.4);
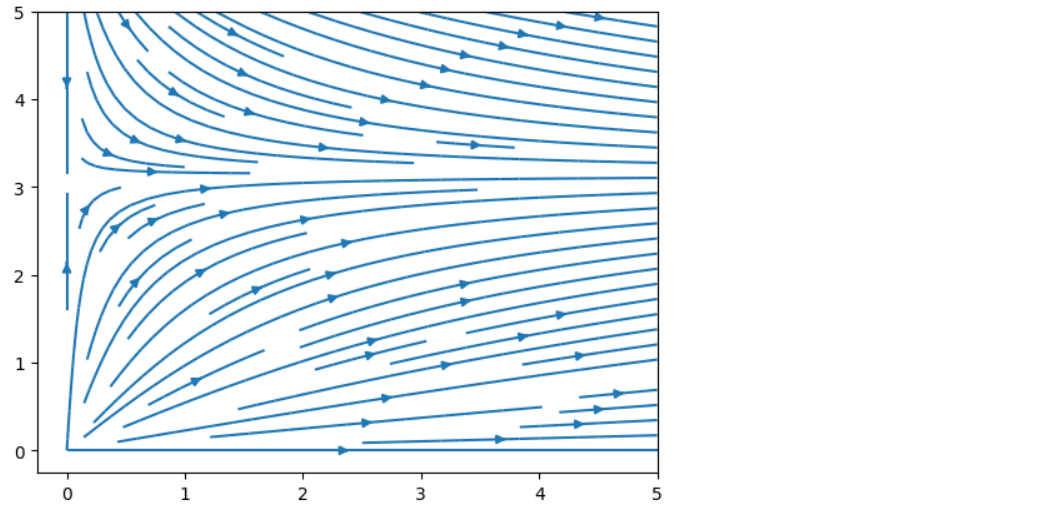
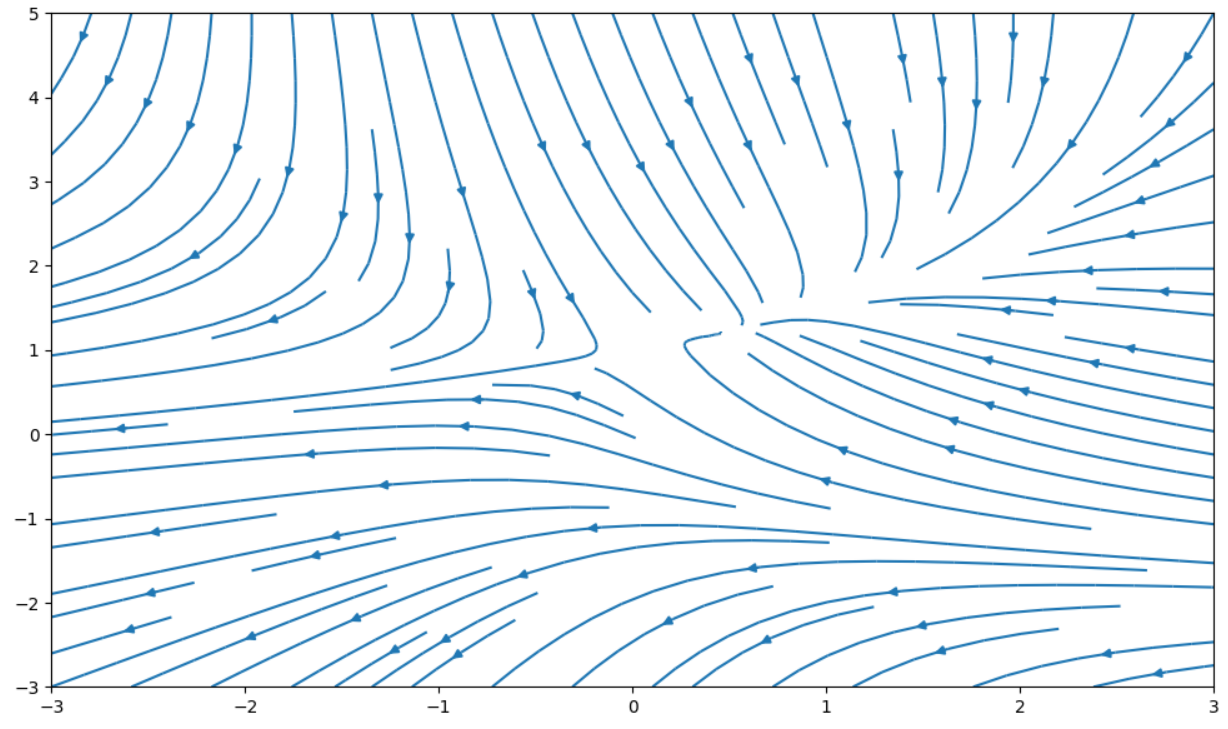
스트림 플롯(Stream Plot)
Y, X = np.mgrid[0:5:100j, 0:5:100j] U = X V = np.sin(Y) plt.streamplot(X,Y,U,V);
Y, X = np.mgrid[-3:5:100j, -3:3:100j] U = -1 - X ** 2 + Y V = 1 + X - Y ** 2 speed = np.sqrt(U**2 + V**2) plt.figure(figsize=(12,7)) plt.streamplot(X,Y,U,V, density=1);
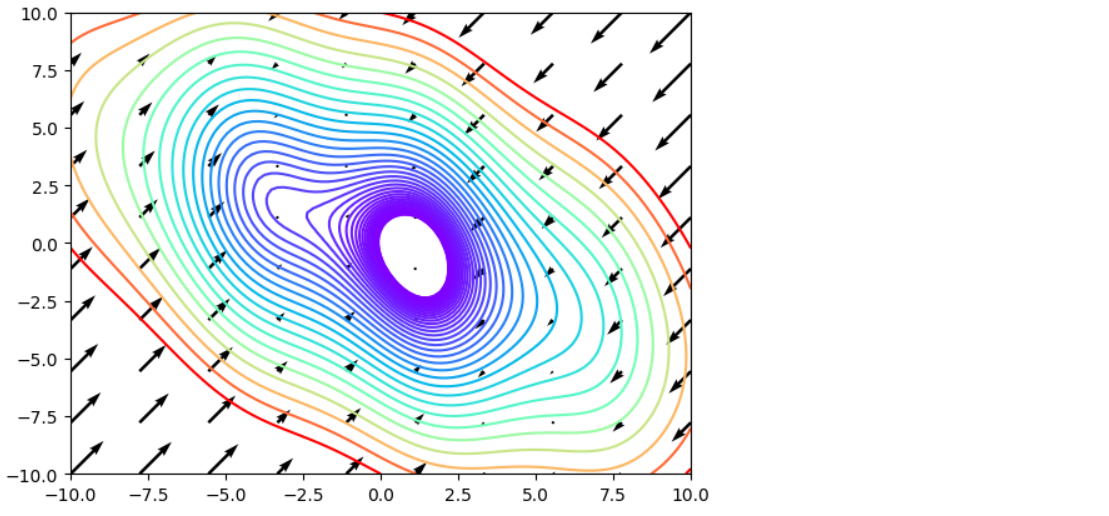
화살표 2차원 필드(quiver)
import sympy # x, y = sympy.symbols('x y') f = x**2 + y**2 + x*y - sympy.sin(x) * 4 fdx = sympy.diff(f,x) fdy = sympy.diff(f,y) # sample_size = 100 xs, ys = np.meshgrid(np.linspace(-10, 10, sample_size), np.linspace(-10, 10, sample_size)) # zs = [float(f.subs(x, xv).subs(y,yv)) for xv, yv in zip(xs.ravel(), ys.ravel())] zs = np.array(zs).reshape(sample_size, sample_size) # plt.contour(xs, ys, zs, 40, levels=np.logspace(-0.5, 2.0, 40), cmap='rainbow') # xs_q, ys_q = np.meshgrid(np.linspace(-10,10,10), np.linspace(-10,10,10)) # xsg = [-float(fdx.subs(x, xv).subs(y,yv)) for xv, yv in zip(xs_q.ravel(), ys_q.ravel())] ysg = [-float(fdx.subs(x, xv).subs(y,yv)) for xv, yv in zip(xs_q.ravel(), ys_q.ravel())] # plt.quiver(xs_q, ys_q, xsg, ysg, width=0.005, scale=500, color='black');
파이 차트(Pie Chart)
- 원그래프, 파이차트는 전체에 대한 각 부분의 비율을 부채꼴 모양으로 나타낸 그래프
- 각 부채꼴의 중심각이 전체에서 차지하는 비율을 나타내며, 비율을 한눈에 볼 수 있다는 장점
- 전체적인 비율을 쉽게 파악할 수 있어서 언론사에서 통계 수치를 공개할 때 자주 활용
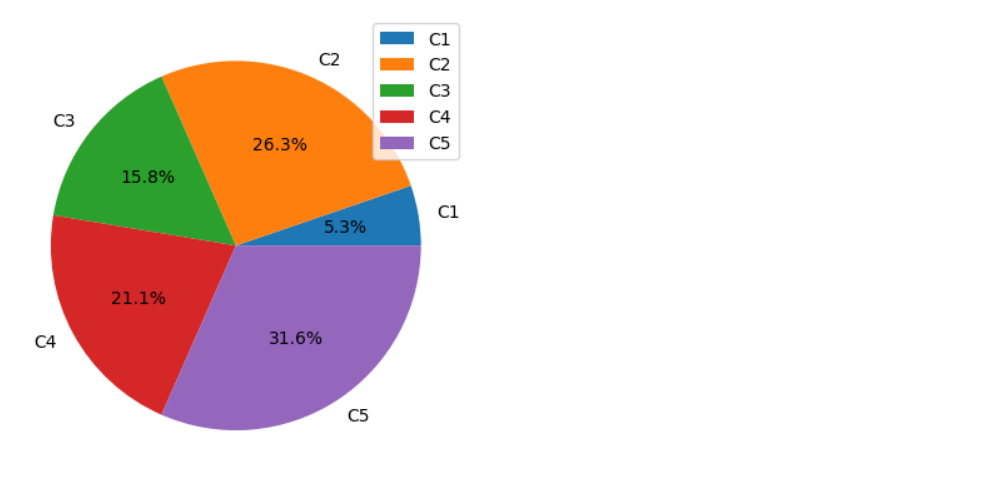
data = [10,50,30,40,60] categories = ['C1', 'C2', 'C3', 'C4', 'C5'] plt.pie(data, labels=categories, autopct = '%0.1f%%') plt.legend(categories);
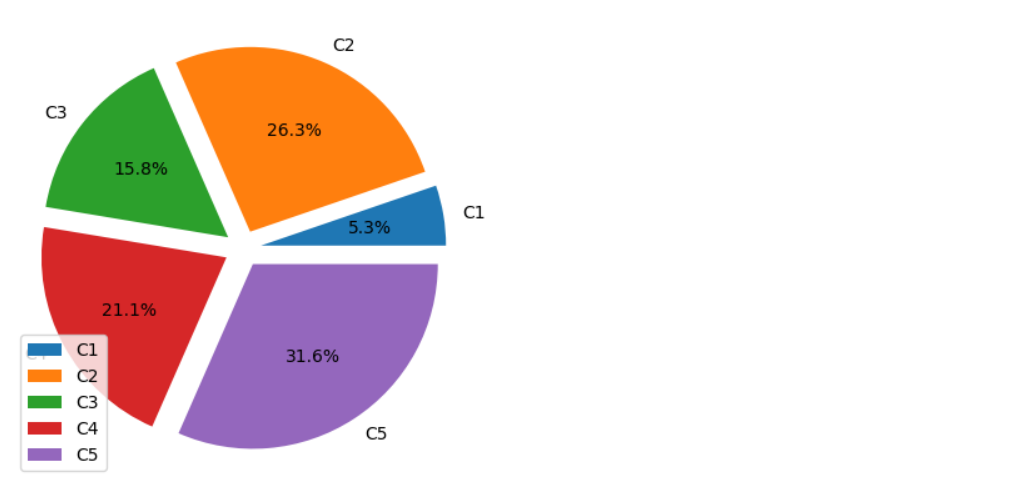
explode = [0.1, 0.1, 0.1, 0.1, 0.1] plt.pie(data, explode=explode, labels=categories, autopct = '%0.1f%%') plt.legend(categories);
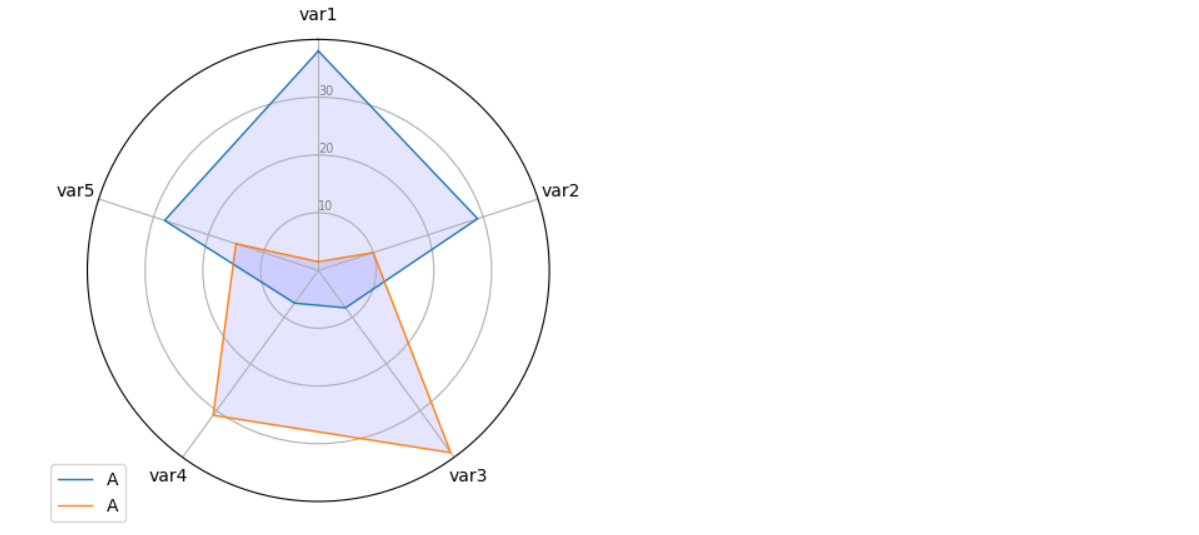
레이다 차트(Radar Chart)
- 어떤 측정 목표에 대한 평가항목이 여러 개일 때 항목 수에 따라 원을 같은 간격으로 나누고, 중심으로부터 일정 간격으로 동심으로 척도를 재는 칸을 나누어 각 평가항목의 정량화된 점수에 따라 그 위치에 점을 찍고 평가항목간 점을 이어 선으로 만들어 항목 간 균형을 한눈에 볼 수 있도록 해주는 도표
- 여러 측정 목표를 함께 겹쳐 놓아 비교하기에도 편리 각 항목 간 비율뿐만 아니라 균형과 경향을 직관적으로 알 수 있어 편리
df = pd.DataFrame({ 'group': ['A', 'B', 'C', 'D'], 'var1' : [38, 1.5, 30, 4], 'var2' : [29, 10, 9, 34], 'var3' : [8, 39, 23, 24], 'var4' : [7, 31, 33, 14], 'var5' : [28, 15, 32, 14] }) # categories = list(df)[1:] N = len(categories) # angles = [n / float(N) * 2 * np.pi for n in range(N)] angles += angles[:1] # ax = plt.subplot(111, polar=True) ax.set_theta_offset(np.pi/2) ax.set_theta_direction(-1) ax.set_rlabel_position(0) plt.xticks(angles[:-1], categories) plt.yticks([10,20,30], ["10", "20", "30"], color='gray', size=7) plt.ylim(0,40) # values = df.loc[0].drop('group').values.flatten().tolist() values += values[:1] ax.plot(angles, values, linewidth = 1, linestyle = 'solid', label='A') ax.fill(angles, values, 'b', alpha=0.1) # values = df.loc[1].drop('group').values.flatten().tolist() values += values[:1] ax.plot(angles, values, linewidth = 1, linestyle = 'solid', label='A') ax.fill(angles, values, 'b', alpha=0.1) # plt.legend(bbox_to_anchor=(0.1, 0.1))
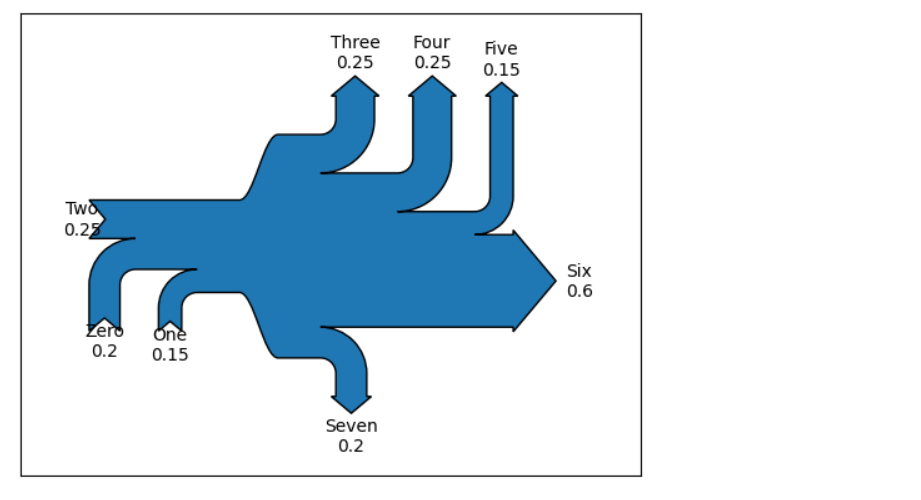
생키 다이어그램(Sankey Diagram)
- 흐름(Flow) 다이어그램의 한 종류로서 그 화살표의 너비로 흐름의 양을 비율적으로 보여줌
from matplotlib.sankey import Sankey # Sankey(flows=[0.20, 0.15, 0.25, -0.25, -0.25, -0.15, -0.60, -0.20], labels=['Zero', 'One', 'Two', 'Three', 'Four', 'Five', 'Six', 'Seven'], orientations = [-1, -1, 0, 1, 1, 1, 0, -1]).finish();
3차원 플로팅(Three-Dimesional Plotting)
from mpl_toolkits import mplot3d
fig = plt.figure() ax = plt.axes(projection = '3d')
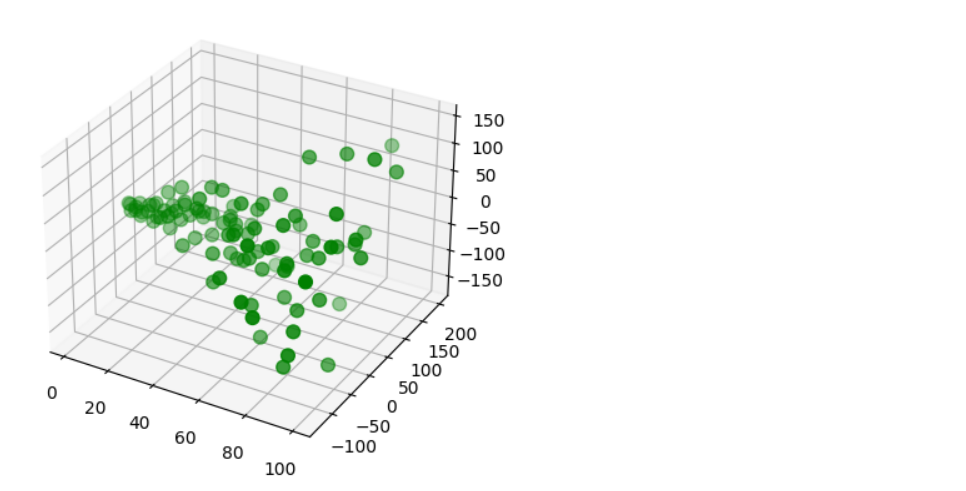
x = range(1, 101) y = np.random.randn(100) * x z = np.random.randn(100) * x # fig = plt.figure() ax = fig.add_subplot(111, projection='3d') ax.scatter(x,y,z,c = 'green', s=60);
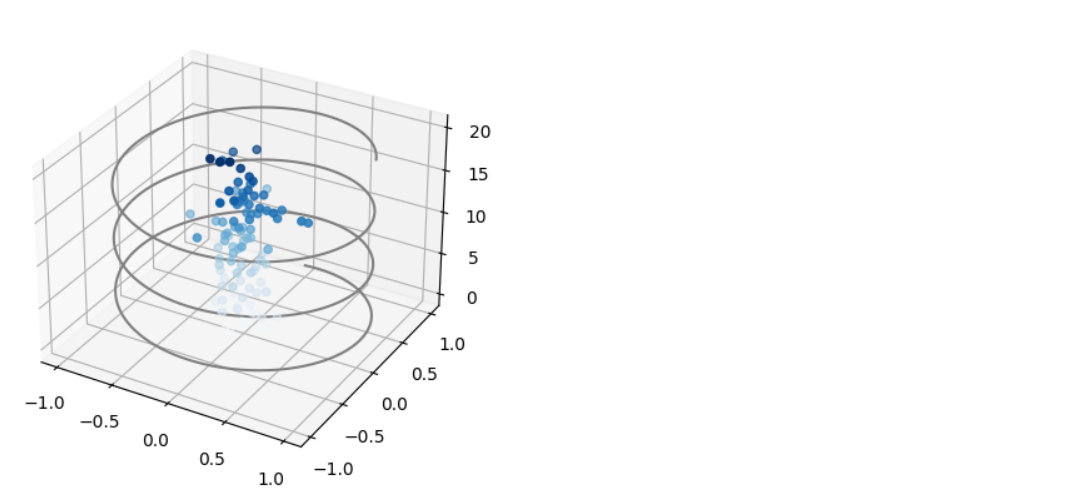
ax = plt.axes(projection='3d') # zline = np.linspace(0,20,1000) xline = np.sin(zline) yline = np.cos(zline) ax.plot3D(xline, yline, zline, 'gray') # zdata = 20 * np.random.random(100) xdata = np.sin(zdata) * 0.2 * np.random.randn(100) ydata = np.cos(zdata) * 0.2 * np.random.randn(100) ax.scatter3D(xdata, ydata, zdata, c=zdata, cmap='Blues');
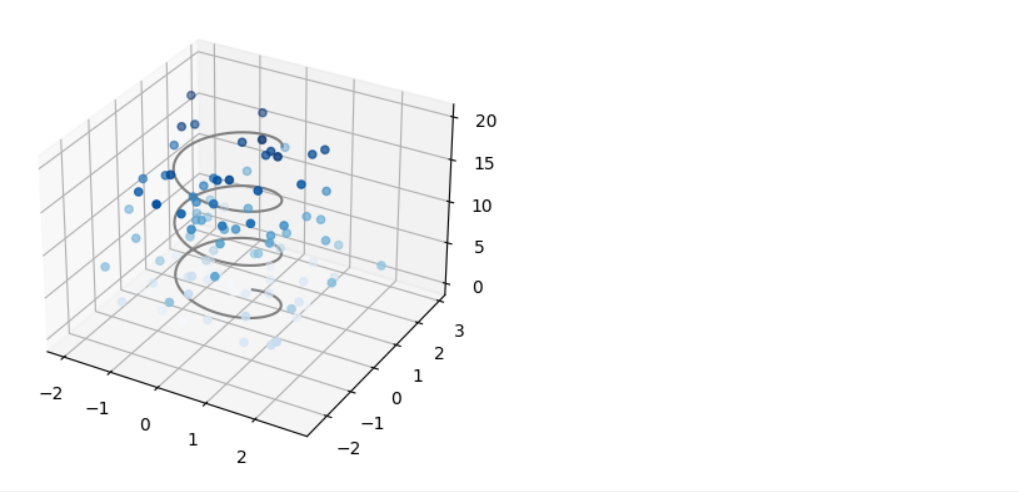
ax = plt.axes(projection='3d') # zline = np.linspace(0,20,1000) xline = np.sin(zline) yline = np.cos(zline) ax.plot3D(xline, yline, zline, 'gray') # zdata = 20 * np.random.random(100) xdata = np.sin(zdata) * 0.2 + np.random.randn(100) ydata = np.cos(zdata) * 0.2 + np.random.randn(100) ax.scatter3D(xdata, ydata, zdata, c=zdata, cmap='Blues');
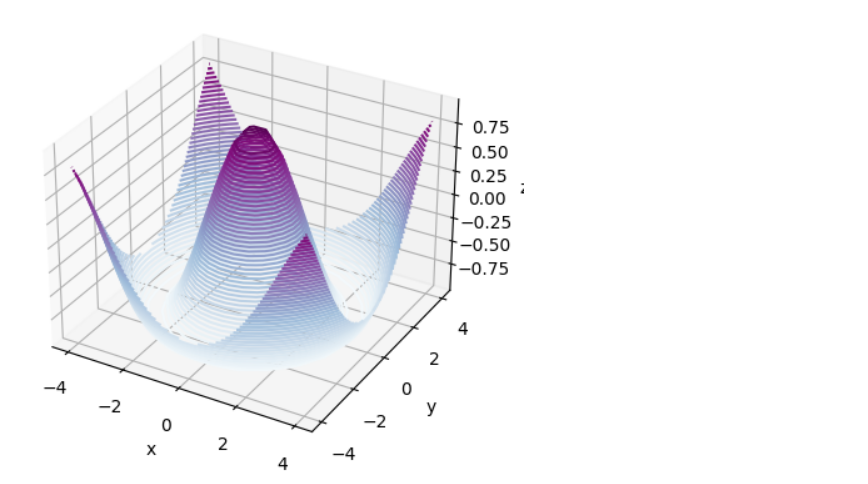
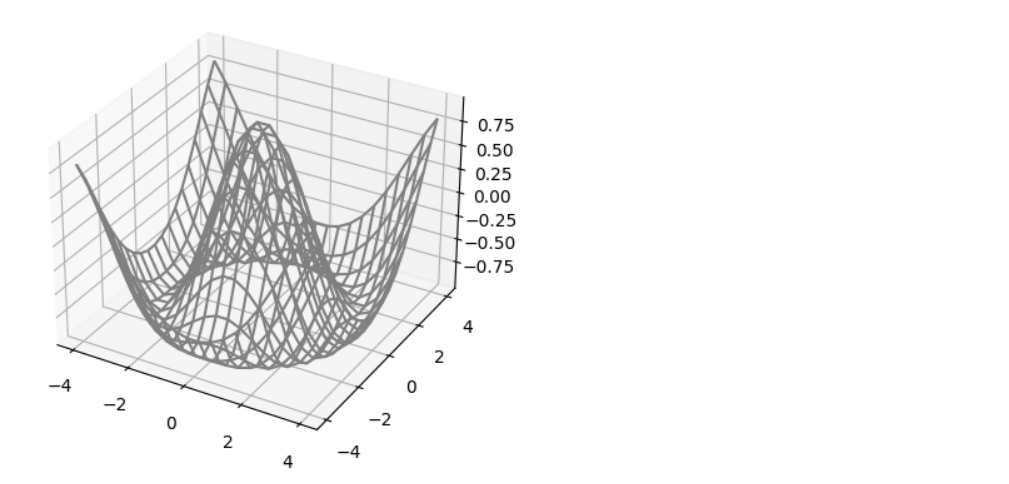
def f(x,y): return np.cos(np.sqrt(x**2 + y**2)) # l = np.linspace(-4, 4, 20) X, Y = np.meshgrid(l,l) Z = f(X, Y)fig = plt.figure() ax = plt.axes(projection = '3d') ax.contour3D(X, Y, Z, 50, cmap='BuPu') ax.set_xlabel('x') ax.set_ylabel('y') ax.set_zlabel('z')
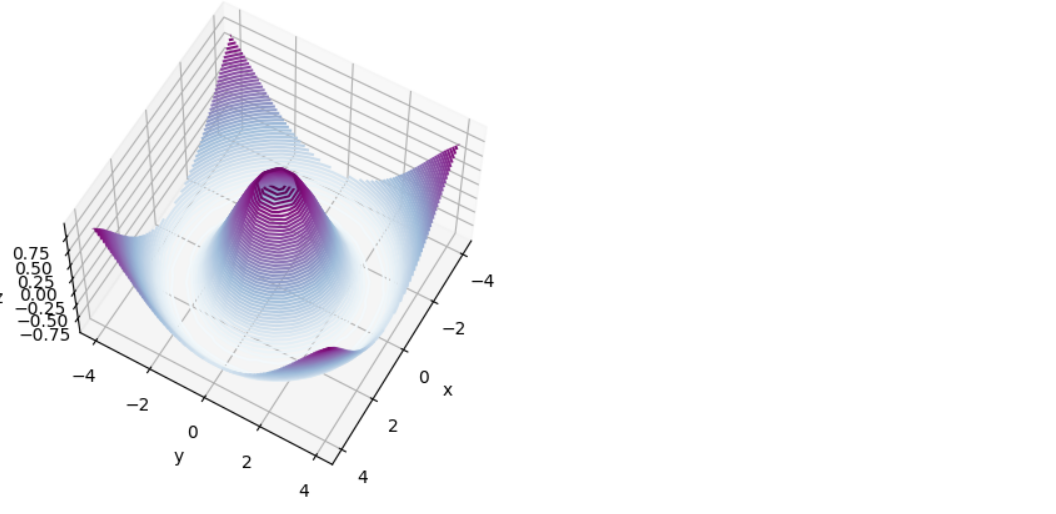
ax.view_init(60,30) fig
fig = plt.figure() ax = plt.axes(projection='3d') ax.plot_wireframe(X, Y, Z, color='gray')
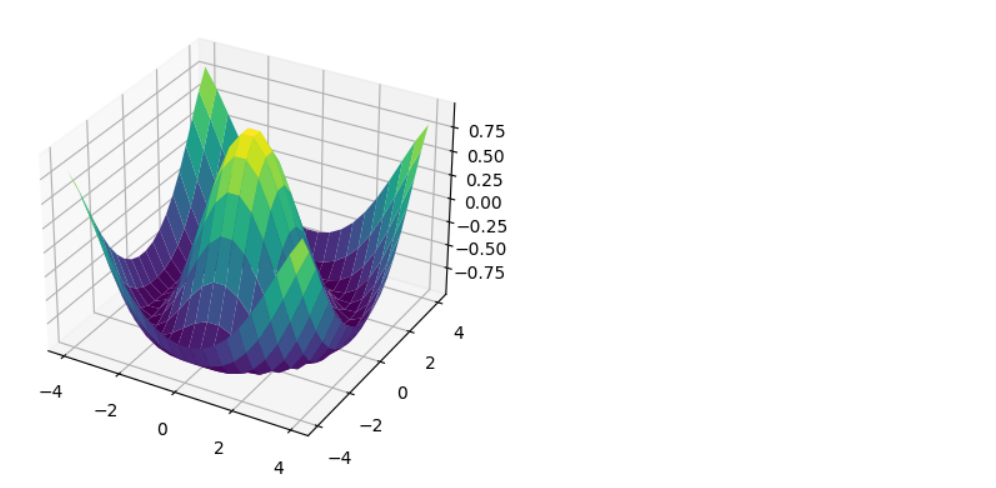
ax = plt.axes(projection='3d') ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap='viridis', edgecolor='none')
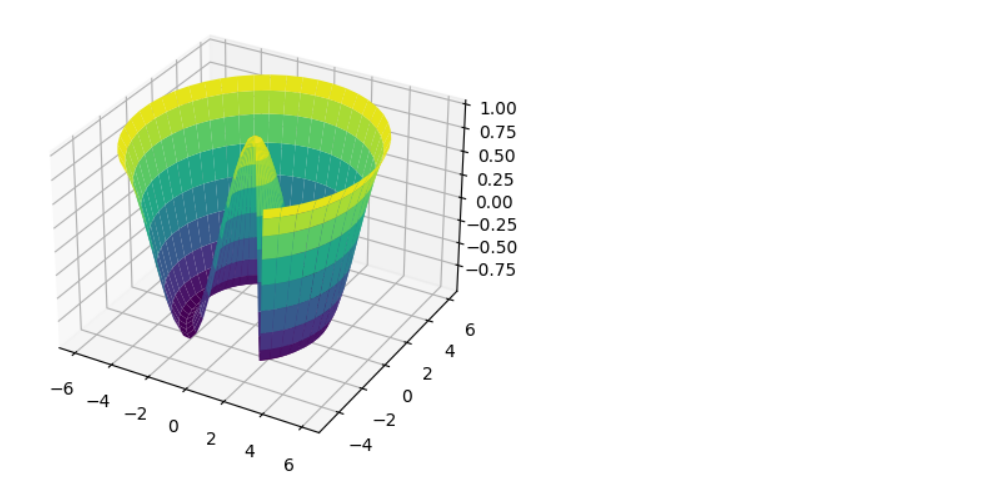
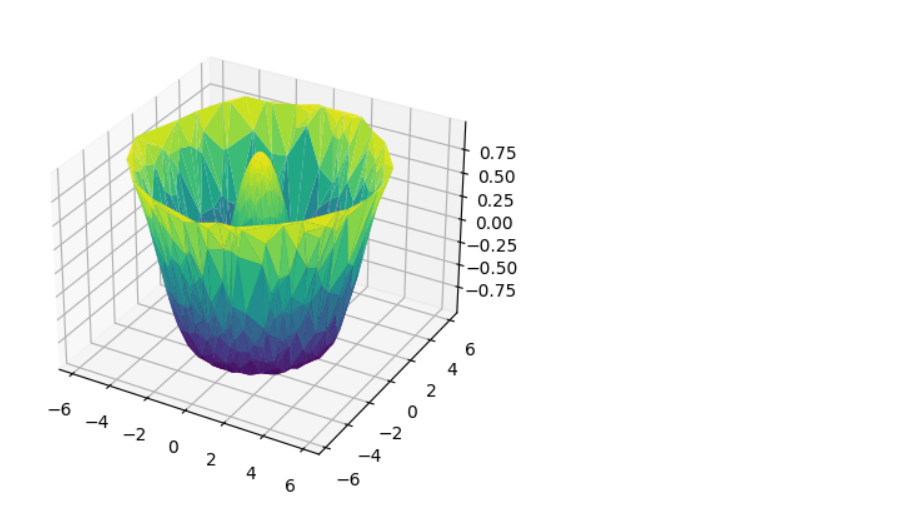
r = np.linspace(0,6,20) theta = np.linspace(-0.8 * np.pi, 0.8*np.pi, 40) r,theta = np.meshgrid(r, theta) # X = r * np.sin(theta) Y = r * np.cos(theta) Z = f(X, Y) # ax = plt.axes(projection='3d') ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap='viridis', edgecolor='none')
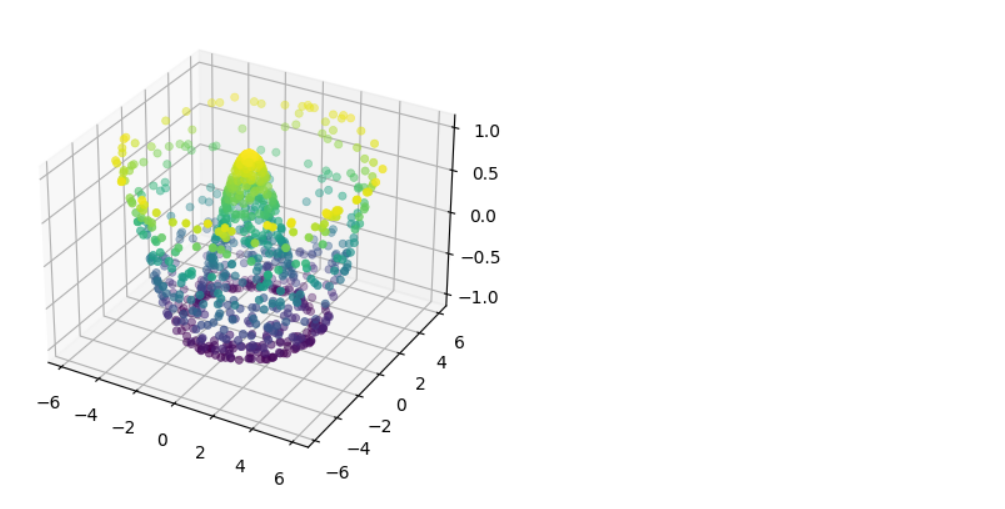
theta = 2 * np.pi * np.random.random(1000) r = 6 * np.random.random(1000) X = np.ravel(r * np.sin(theta)) Y = np.ravel(r * np.cos(theta)) Z = f(X, Y)ax = plt.axes(projection='3d') ax.scatter(X, Y, Z, c=Z, cmap='viridis', linewidth=0.5);
ax = plt.axes(projection='3d') ax.plot_trisurf(X, Y, Z, cmap='viridis', edgecolor='none')
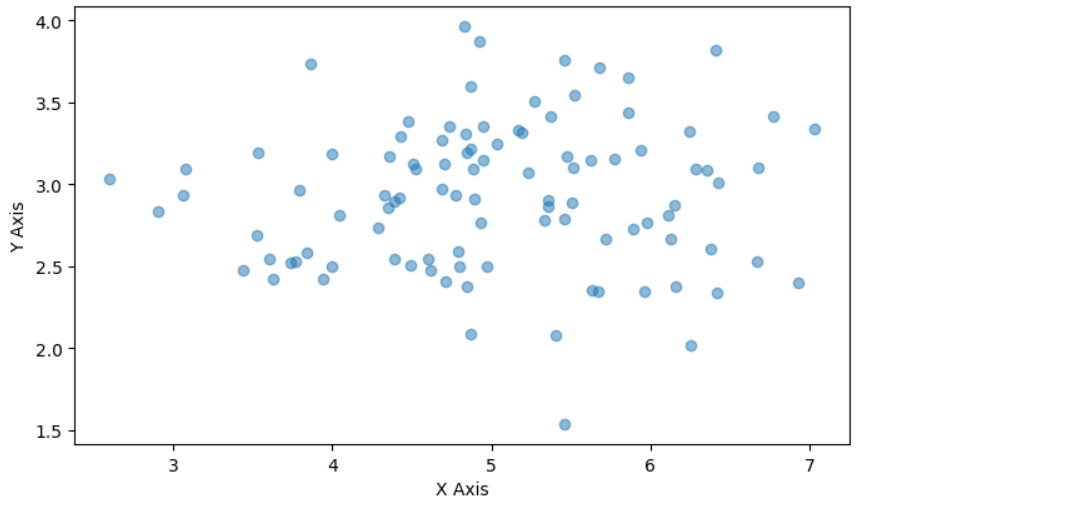
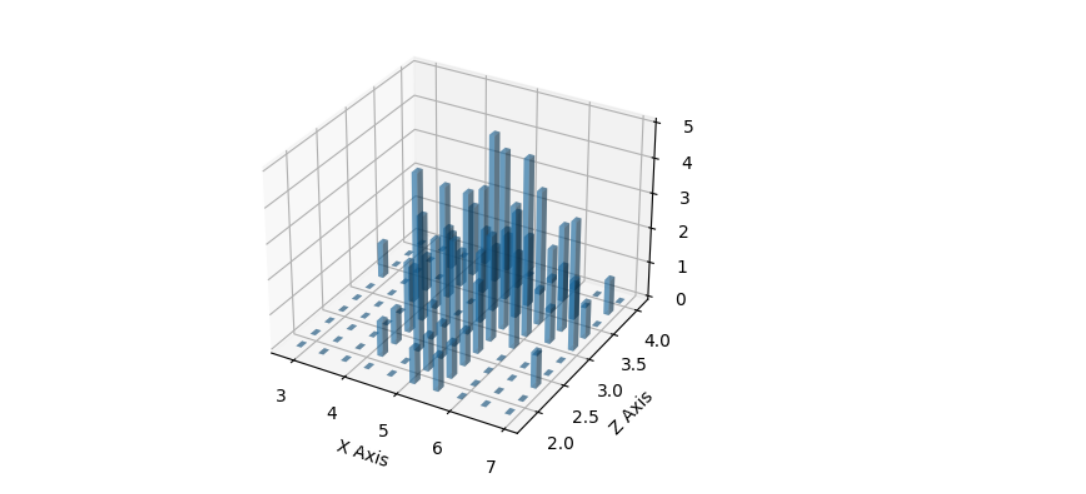
x = np.random.normal(5,1,100) y = np.random.normal(3, 0.5, 100) # fig = plt.figure(figsize=(8,10)) hist, xedges, yedges = np.histogram2d(x,y,bins=10) # elements = (len(xedges) - 1) * (len(yedges) - 1) xpos, ypos = np.meshgrid(xedges[:-1]+0.25, yedges[:-1]+0.25) xpos = xpos.flatten() ypos = ypos.flatten() zpos = np.zeros(elements) # dx = 0.1 * np.ones_like(zpos) dy = dx.copy() dz = hist.flatten() # ax = fig.add_subplot(211) ax.scatter(x, y, alpha = 0.5) ax.set_xlabel('X Axis') ax.set_ylabel('Y Axis') # ax2 = fig.add_subplot(212, projection = '3d') ax2.bar3d(xpos, ypos, zpos, dx, dy, dz, alpha=0.4) ax2.set_xlabel('X Axis') ax2.set_ylabel('Y Axis') ax2.set_ylabel('Z Axis')
Reference : 이수안컴퓨터연구소 강의 : Matplotlib 한 번에 제대로 배우기 실습 자료 및 강의자료