난이도 : 골드 4
유형 : 최소신장트리
https://www.acmicpc.net/problem/1197
문제
그래프가 주어졌을 때, 그 그래프의 최소 스패닝 트리를 구하는 프로그램을 작성하시오.
최소 스패닝 트리는, 주어진 그래프의 모든 정점들을 연결하는 부분 그래프 중에서 그 가중치의 합이 최소인 트리를 말한다.
입력
첫째 줄에 정점의 개수 V(1 ≤ V ≤ 10,000)와 간선의 개수 E(1 ≤ E ≤ 100,000)가 주어진다. 다음 E개의 줄에는 각 간선에 대한 정보를 나타내는 세 정수 A, B, C가 주어진다. 이는 A번 정점과 B번 정점이 가중치 C인 간선으로 연결되어 있다는 의미이다. C는 음수일 수도 있으며, 절댓값이 1,000,000을 넘지 않는다.
그래프의 정점은 1번부터 V번까지 번호가 매겨져 있고, 임의의 두 정점 사이에 경로가 있다. 최소 스패닝 트리의 가중치가 -2,147,483,648보다 크거나 같고, 2,147,483,647보다 작거나 같은 데이터만 입력으로 주어진다.
출력
첫째 줄에 최소 스패닝 트리의 가중치를 출력한다.
해결 아이디어
그래프가 주어졌을 때, 최소 스패닝 트리의 가중치를 출력하는 문제이다.
우선 MST(최소 스패닝 트리) 개념을 알아보자.
스패닝 트리: 그래프의 모든 정점을 연결하는 트리(사이클이 없고, 모든 정점을 포함).
최소 스패닝 트리(MST): 스패닝 트리 중 간선 가중치 합이 최소인 것.
조건:
- 모든 정점을 포함
- 사이클이 없어야 함
- 간선의 가중치 합이 최소
예제 1
3 3
1 2 1
2 3 2
1 3 3
을 그림을 그려보면
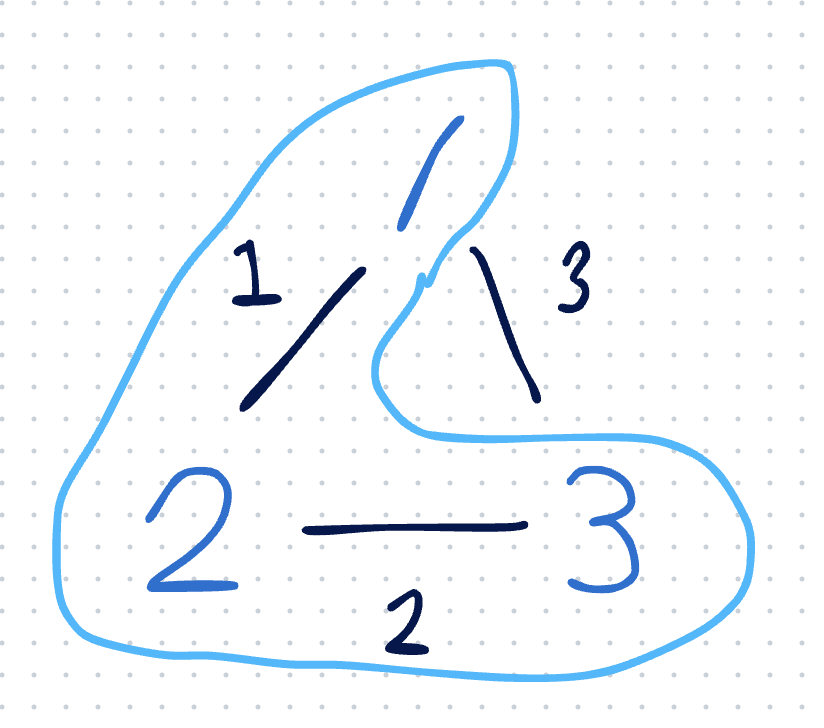
이렇게 1,2,3 사이클이 있는 그래프가 있는 와중, 모든 노드를 연결하되 사이클이 없는 , 그리고 간선의 가중치의 합이 최소인 트리인, 최소 스패닝 트리를 찾으면 된다.
예제에선 하늘색으로 감싸진 1-2-3 순으로 이어진 트리가 가중치가 3으로 최소인 MST가 된다.
어떻게 풀까?
이 문제를 푸는 알고리즘 유형은 두 개가 있다고 한다.
1. 크루스칼 (Kruskal)
- 아이디어: 가장 가중치가 작은 간선부터 차례대로 선택하면서, 사이클이 생기지 않으면 포함
- 유니온 파인드 활용
- 프림 (Prim)
- 아이디어: 하나의 정점에서 시작해서, MST에 포함되지 않은 정점 중 가장 가까운 정점을 하나씩 추가.
- 우선순위 큐(heapq) 사용
오늘은 먼저 유니온 파인드를 활용하는 크루스칼 알고리즘으로 풀려 한다.
크루스칼 알고리즘은 그래프 중심 알고리즘이 아니라 간선 중심 알고리즘이라
입력을
graph = [ [] for _ in range(V+1)]
for _ in range(E):
A, B, C = map(int,input().split())
graph[A].append((B, C))
graph[B].append((A, C))이런식으로 그래프를 받지 않고 간선을 ( 가중치, u, v ) 순으로 받고 가중치를 기준으로 정렬한다.
edges = []
for _ in range(E):
u, v, w = map(int,input().split())
edges.append((w, u, v))
edges.sort() # 가중치 기준 오름차순그 다음은 Union-Find(서로소 집합) 자료구조를 초기화하고,
각 노드의 부모를 자기 자신으로 설정해준다.
랭크(rank) 배열은 트리의 높이를 저장해서, 두 집합을 합칠 때 더 낮은 트리를 높은 트리에 붙이기 위해 사용된다.
parent = [i for i in range(V + 1)]
rank = [0] * (V + 1)union(a, b) 함수는 a와 b가 속한 집합을 합치는 역할을 한다.
루트가 같으면 이미 같은 집합이므로 False를 반환해 간선을 추가하지 않고,
루트가 다르면 랭크를 비교해서 더 낮은 쪽을 높은 쪽에 붙인다.
def union(a, b):
ra, rb = find(a), find(b)
if ra == rb:
return False # 같은 집합이면 합치지 않음 (사이클 발생)
if rank[ra] < rank[rb]:
parent[ra] = rb
elif rank[ra] > rank[rb]:
parent[rb] = ra
else:
parent[rb] = ra
rank[ra] += 1
return True이제 크루스칼의 핵심 로직이다.
간선 리스트를 앞에서부터(=가중치가 작은 순서대로) 하나씩 꺼내서,
union이 성공하면 MST에 포함시키고 가중치를 더한다.
MST의 간선 개수가 정점-1개가 되면 모든 정점이 연결된 것이므로 종료한다.
mst_weight = 0
picked = 0
for w, u, v in edges:
if union(u, v):
mst_weight += w
picked += 1
if picked == V - 1: # MST 완성
break
print(mst_weight)전체 코드
import sys
input = sys.stdin.readline
V, E = map(int,input().split())
# 간선 중심 알고리즘이라 그래프 말고 간선을 리스트로 받음. (가중치, u, v) 형태로 저장후 정렬
edges = []
for _ in range(E):
u, v, w = map(int,input().split())
edges.append((w, u, v))
edges.sort() # 가중치 기준 오름차순
# 유니온 파인드
parent = [i for i in range(V + 1)]
rank = [0] * (V + 1) # 트리의 높이
def find(x):
if parent[x] != x:
parent[x] = find(parent[x])
return parent[x]
def union(a, b):
root_a , root_b = find(a), find(b)
if root_a == root_b :
return False # 이미 같은 집합 -> 사이클 생김
# 트리 높이 기준 합치기
if rank[root_a] < rank[root_b] :
parent[root_a] = root_b
elif rank[root_a] > rank[root_b]:
parent[root_b] = root_a
else:
parent[root_b] = root_a
rank[root_a] += 1
return True
# 크루스칼 : 가중치 작은 것부터 넣으며 간선의 개수 = 노드의 개수 -1 이면 종료
mst_weight = 0
picked = 0
for w, u , v in edges:
if union(u, v):
mst_weight += w
picked += 1
if picked == V - 1 :
break
print(mst_weight)