3665번: 최종 순위 [python]

난이도 : 골드 1
유형 : 위상정렬
https://www.acmicpc.net/problem/3665

---

문제 접근

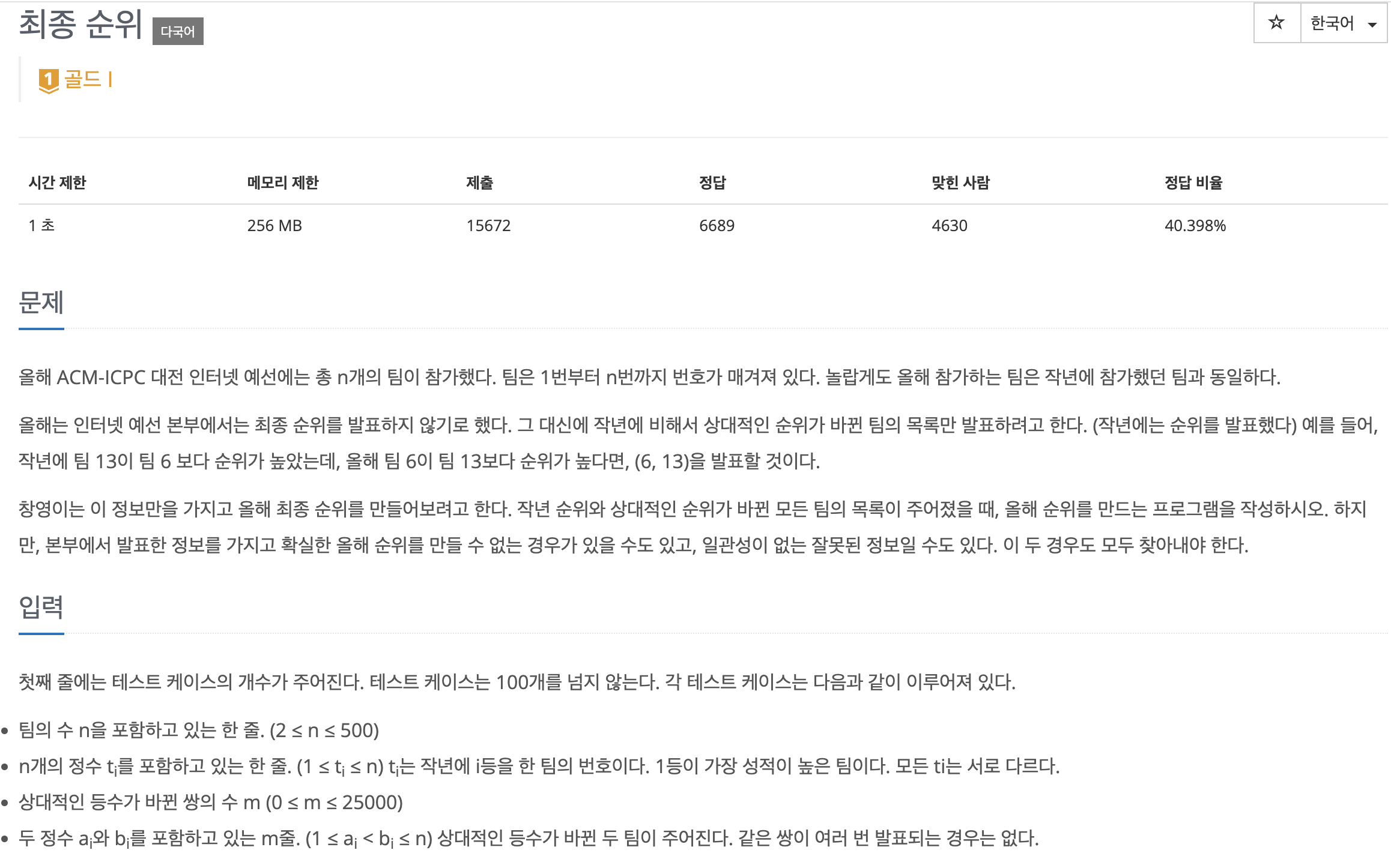
작년 순위와 상대적인 순위가 바뀐 모든 팀의 목록이 주어졌을 때, 올해 순위를 만드는 프로그램을 작성하시오.

상대 순위를 가지고 최종 순위를 만든다?
-> 위상정렬을 떠올린다.

입력은 총 3 + m 줄을 받는다.
1. 팀의 수 n
2. 작년 순위 1등부터 n등까지.
3. 순위가 바뀐 팀 쌍의 수 m
m. 바뀐 쌍 m줄

구현 절차

1. 입력받기
2. 그래프 및 진입차수 초기화
3. 변경된 순위 반영 (간선 뒤집기)
4. 위상 정렬 수행
5. 출력

해답 및 풀이

from collections import deque
import sys
input = sys.stdin.readline

T = int(input())

for _ in range(T):
    
    # 1. 입력 받기 n: 팀수, last_rank : 작년 순위, m: 바뀐 팀 쌍의 수, changes: 바뀐 팀 쌍
    n = int(input()) 
    last_rank = list(map(int,input().split()))
    m = int(input())
    changes = []

    for _ in range(m):
        change = tuple(map(int,input().split()))
        changes.append(change)

    # 2. 그래프 및 진입 차수 초기화
    graph = []
    for _ in range(n + 1):
        row = []
        for _ in range(n + 1):
            row.append(False)
        graph.append(row)

    indegree = [0] * (n + 1)


    # 작년 순위를 바탕으로 모든 쌍 간 간선 만들기 i가 j보다 먼저니까
    for i in range(n):
        for j in range(i + 1, n):
            higher = last_rank[i] # higher 설정
            lower = last_rank[j] # lower 설정
            graph[higher][lower] = True  # 방향 간선 추가
            indegree[lower] += 1 # lower는 선행되어야 할 팀이 하나 더 있는 것이니 진입 차수 1 증가


    #3. 변경된 순위 반영 ( 간선 뒤집기 )
    # 순위 변경은 간선을 반대로 바꾸는 것 + 진입 차수 조정
    for a, b in changes:
        if graph[a][b] == True: # a -> b 였다면
            graph[a][b] = False
            graph[b][a] = True
            indegree[b] -= 1
            indegree[a] += 1
        
        elif graph[b][a] == True: # b -> a 였다면
            graph[b][a] = False
            graph[a][b] = True
            indegree[a] -= 1
            indegree[b] += 1

    # 4. 위상 정렬 수행
    queue = deque()
    result = [] 

    # 진입차수 0인 노드. 큐에 추가하기
    for i in range(1, n + 1):
        if indegree[i] == 0:
            queue.append(i)

    certain = True # 정답이 유일한 지 판별하는 변수, 중간에 큐에 진입차수 0인 팀이 2개 이상 있으면 복수 정답 가능
    cycle = False # 정답출력이 불가능한 상태인지 판별, 중간에 큐가 비었는데 더 넣을 팀이 없다 => 사이클 발생

    for _ in range(n):
        if len(queue) == 0:
            cycle = True
            break

        if len(queue) > 1:
            certain = False


        # 진입차수 0인 팀 꺼내고 결과 리스트에 추가
        now = queue.popleft()
        result.append(now)


        # now를 꺼냈으니까 간선 지우기, now -> i 간선, i의 진입차수가 0 되었다면? 큐에 추가
        for i in range(1, n+1):
            if graph[now][i]:
                indegree[i] -= 1
                if indegree[i] == 0:
                    queue.append(i)


    # 5. 출력
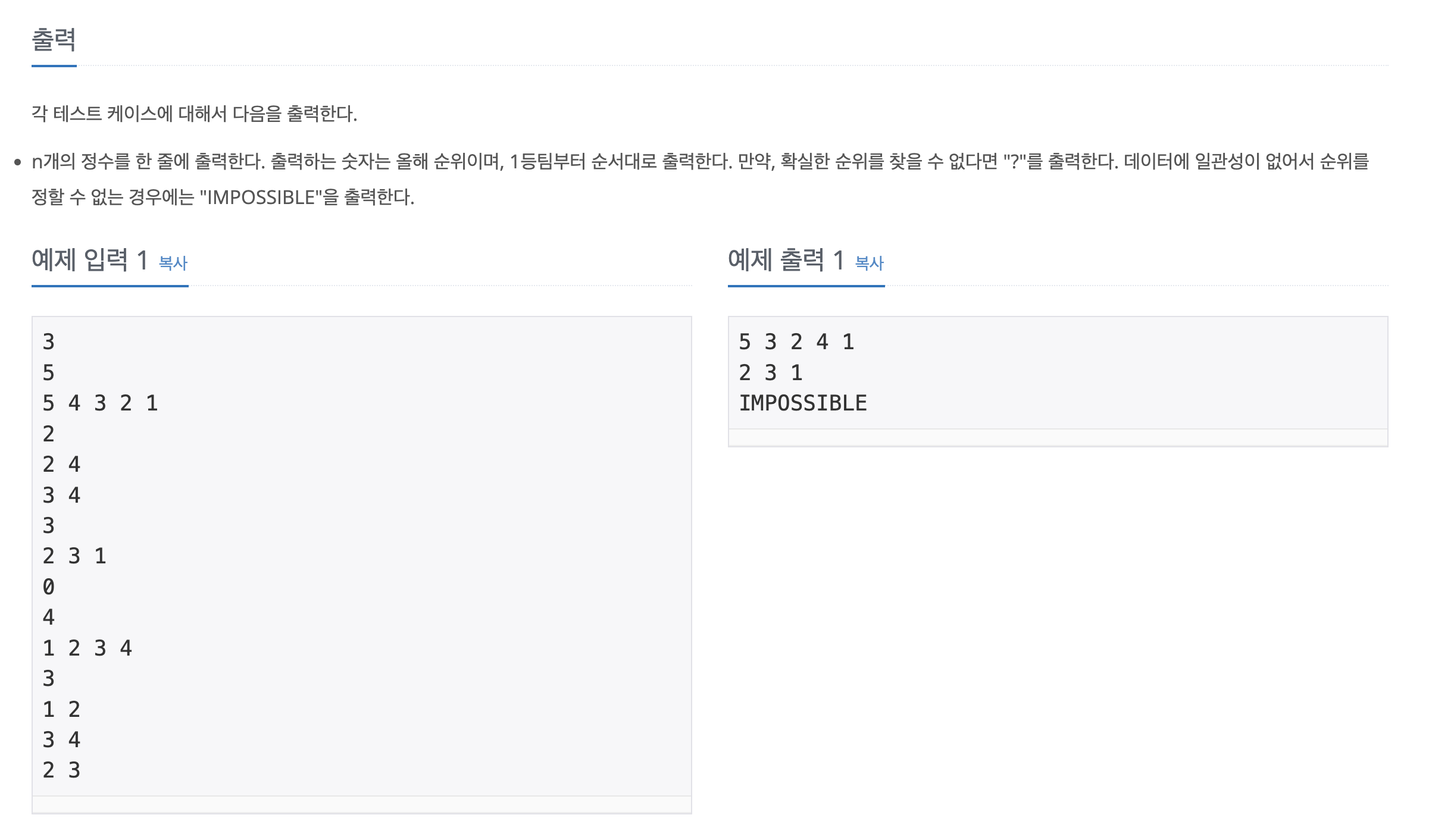
    if cycle == True:
        print("IMPOSSIBLE")
    elif certain == False:
        print("?")
    else:
        print(' '.join(map(str, result)))

이 문제는 "선후관계가 정해진 순위 정보를 방향 그래프로 바꾸고, 일부 간선을 뒤집으며 위상 정렬로 최종 순위를 추론하는 문제" 였다.

간선의 저장에는 '인접 리스트'와 '인접 행렬' 방식이 있는데 주로 '인접 리스트' 방식으로 풀어와서 2차원 배열을 생성해 True, False 로 저장하는 인접 행렬 방식이 익숙하지 않았다.

위 문제에선
모든 정점 쌍을 비교해서 간선을 뒤집었어야 했고
graph[a][b] 여부를 빠르게 확인했어서 인접행렬 방식이 더 적절했다.

비교

항목	인접 리스트 (Adjacency List)	인접 행렬 (Adjacency Matrix)
그래프 크기	정점 수 $N$ 많고 간선 수 적을 때 (희소 그래프)	정점 수 $N$ 적고 간선 수 많을 때 (밀집 그래프)
공간 복잡도	$O(N + M)$ (M: 간선 수)	$O(N^2)$
간선 탐색	정점 $u$에서 나가는 간선만 탐색: 빠름 $O(\text{간선 수})$	항상 모든 $N$ 확인: 느림
간선 존재 확인 (u→v)	$O(\text{리스트 길이})$, 느릴 수 있음	$O(1)$, 매우 빠름
간선 추가/삭제	리스트에 append/remove	단순한 True/False 할당
구현 복잡도	직관적이고 효율적	코드 간결하지만 메모리 소모 큼
예시 알고리즘	BFS, DFS, 다익스트라, 위상정렬 등 일반적인 알고리즘	플로이드-워셜, 빠른 간선 존재 확인이 필요한 특수 경우