단조 스택이란?

단조 스택에 대해 알아보겠다.

단조 스택에 '단조'는 단조롭다 할때의 단조이다.

수학에서 단조(monotone)란, 수열이나 함수가 한 방향으로만 변하는 걸 말한다.

즉, 계속 증가만 하거나, 계속 감소만 하는 성질을 뜻한다.

그렇다면 단조 스택은?

스택에 저장된 값들이 단조 증가/감소 순서를 유지하는 자료구조이다.

스택의 위에서부터 아래까지 항사 오름차순이거나 내림차순으로 정렬된 상태를 유지하는 스택이다.

새로운 값이 들어올때, 이 순서를 깨뜨리는 원소들은 pop하면서 정리하는 방식이다.

• 단조(monotone) = 한 방향으로만 변함.
• 단조 증가: 앞에서 뒤로 갈수록 값이 같거나 커짐 (1 ≤ 2 ≤ 2 ≤ 3).
• 단조 감소: 앞에서 뒤로 갈수록 값이 같거나 작아짐 (10 ≥ 7 ≥ 7 ≥ 3).

이 감각 그대로 “스택 내부가 항상 단조(증가/감소) 상태”가 되도록 유지하는 게 단조 스택.

단조 스택의 핵심 아이디어

• 새 값이 들어올 때 단조성을 깨는 값들을 pop해서 정리.
• 각 원소는 최대 한 번 push, 한 번 pop → 전체 O(N).
• “앞/뒤에서 가장 가까운 더 큰/작은 값”을 찾는 데 유용하다.

---

단조 증가 스택 (Monotone Increasing Stack)

스택 안의 값이 위에서 아래로 갈수록 커지는(오름차순) 형태.

스택에 새로운 값이 들어올 때, 이 element는 스택에 저장된 elemeent들보다 크거나 같아야 한다.

새 element의 크기가 stack의 top값 보다 작다면, 새 element보다 작거나 같은 element 를 찾을 때 까지 혹슨 스택이 비어있을 때 까지 계속 pop() 해준다.

---

예를 들어 [1,7,9,5]로 저장되어있는 배열이 있고 단조 증가 스택에 넣는다고 가정해보겠다.

1. 왼쪽 1부터 스택에 들어간다.
   stack : [1]

2. 그 다음 7이 들어간다.
   그런데 7은 stack에 top 값 1보다 크니까 별 문제 없이 들어간다.
   stack : [1,7]

3. 9도 마찬가지이다.
   stack:[1,7,9]

4. 그런데 5의 경우
   stack의 top 값 9보다 작다. 그러니 단조 증가 스택에 들어갈 수 없다.
   stack.pop() 을 시킨다.
   stack:[1,7]

그리고 top값과 또 비교한다.

그래도 5가 7보다 작으니 단조 증가 스택에 들어갈 수 없다.

그러니 또 stack.pop()을 한다.

stack:[1]

이제는 5가 push될수 있다.
push()

stack:[1,5]

시간 복잡도 : O(N)

---

단조 감소 스택 (Monotone Decreasing Stack)

스택 안의 값이 위에서 아래로 갈수록 작아지는(내림차순) 형태.

새로운 값이 들어올 때, 기존 값보다 크거나 같은 원소들을 pop해서 정리한다,

주로 다음 더 작은 수(Next Smaller Element, 오작수) 문제에 사용된다.

---

언제 쓰냐?

1) “오른쪽(또는 왼쪽)에 있는 가장 가까운 더 큰/작은 값”

• 키워드: Next Greater/Smaller, Nearest, First larger/smaller to the right/left
• 예: 오큰수, 오작수, 온도/주식 유지일수, 빗물 양 계산 보조

2) “각 원소 기준 범위를 확장/축소해서 넓이/길이를 계산”

• 예: 히스토그램 최대 직사각형(막대를 중심으로 좌우 첫 더 작은 막대까지가 유효 구간)

3) “한 번의 선형 스캔으로 O(N)에 풀어야 할 때”

• 중첩 루프로 풀면 N^2인데, 각 원소를 push/pop 최대 한 번씩만 처리해서 한 바퀴에 끝내고 싶다.

4) “증가/감소 조건을 만족할 때까지 과거 값들을 제거하며 진행”

• 현재 값 기준으로 의미 없어진 과거 값들을 과감히 버려 단조성 확보.

---

다시 이 정리를 기반으로 백준 17928번: 오큰수 를 풀어보겠다.

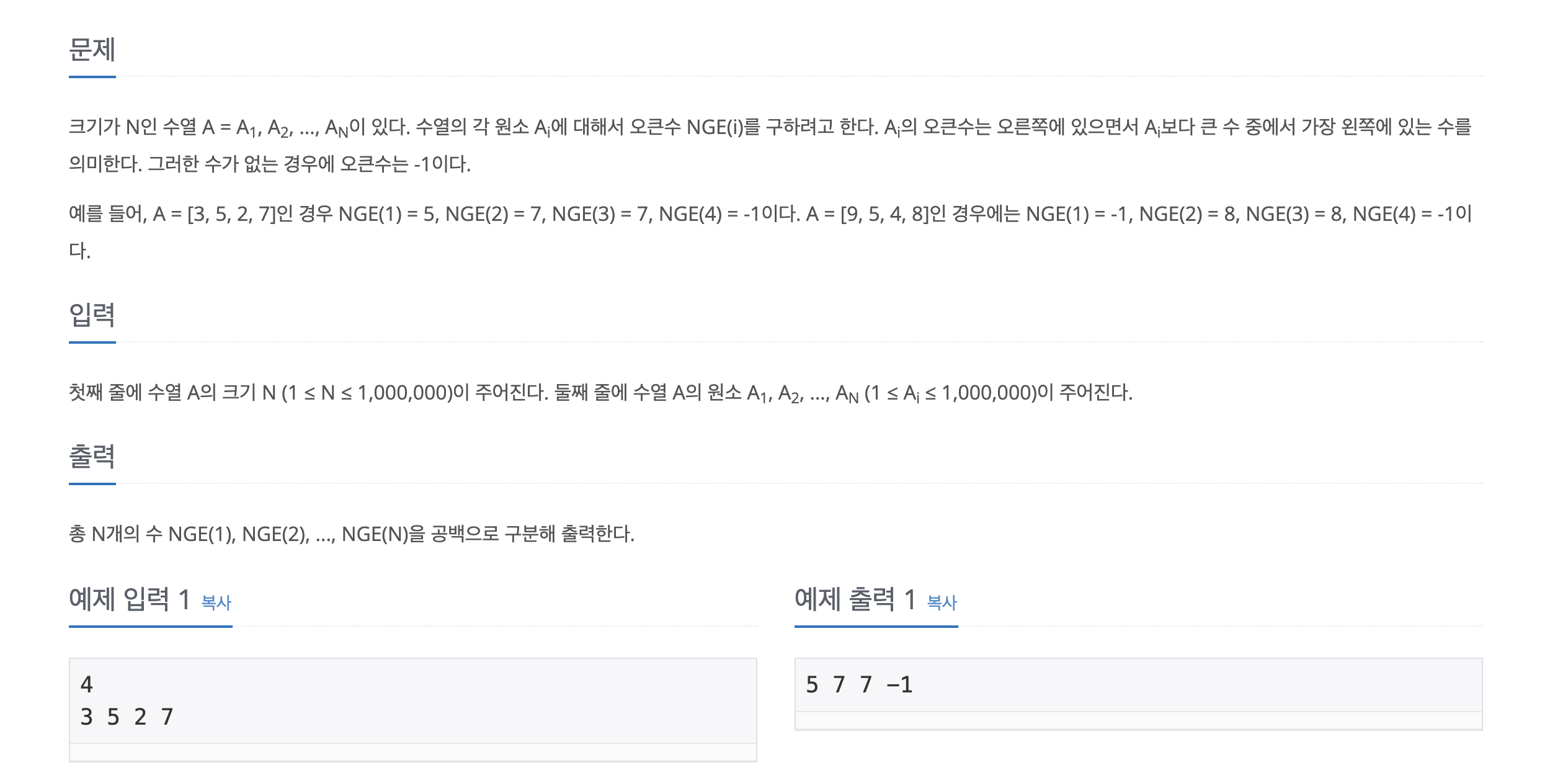
수열 A가 주어졌을 때, 각 원소를 오큰수(NGE: Next Greater Element) 로 바꾸는 문제다.
오큰수란 해당 원소의 오른쪽에 있으면서, 가장 먼저(가장 가까이) 등장하는 ‘더 큰 수’ 를 말한다.
못 찾으면 -1.

단조 감소 스택으로 풀라고 만들어진 문제이다.

• 스택에는 인덱스를 저장한다.
• 스택이 내림차순(값이 큰 → 작은) 이 되도록 유지한다.
• 새 원소 A[i]를 볼 때,
  while stack and A[stack[-1]] < A[i]:
  • 스택 top 인덱스 j를 pop 하고, answer[j] = A[i] 로 채운다. (j의 오큰수는 i번째 값)
• 루프가 끝나고 스택에 남은 인덱스들은 오른쪽에 더 큰 수가 없으므로 -1.

---

• 초기: stack = [], answer = [-1, -1, -1, -1]

1) i=0, A[i]=3

• stack 비어있음 → push
• stack = [0]

2) i=1, A[i]=5

• A[stack[-1]]=A[0]=3 < 5 → pop → answer[0]=5
• stack 비어짐 → push
• stack = [1], answer = [5, -1, -1, -1]

3) i=2, A[i]=2

• A[stack[-1]]=A[1]=5 < 2 → False → push
• stack = [1, 2]

4) i=3, A[i]=7

• A[2]=2 < 7 → pop → answer[2]=7
• A[1]=5 < 7 → pop → answer[1]=7
• stack 비어짐 → push
• stack = [3], answer = [5, 7, 7, -1]

끝. 남은 인덱스 3은 오른쪽에 더 큰 수가 없으니 -1 유지.

---

해답 및 풀이

import sys
input = sys.stdin.readline

N = int(input().strip())
A = list(map(int, input().split()))

answer = [-1] * N
stack = []  # 인덱스를 저장하는 단조 '감소' 스택

for i in range(N):
    # 현재 값이 스택 top 인덱스의 값보다 크면, 그 top의 오큰수는 현재 값
    while stack and A[stack[-1]] < A[i]:
        answer[stack.pop()] = A[i]
    stack.append(i)

# 스택에 남은 인덱스는 오른쪽에 더 큰 수가 없으므로 -1 그대로
print(*answer)